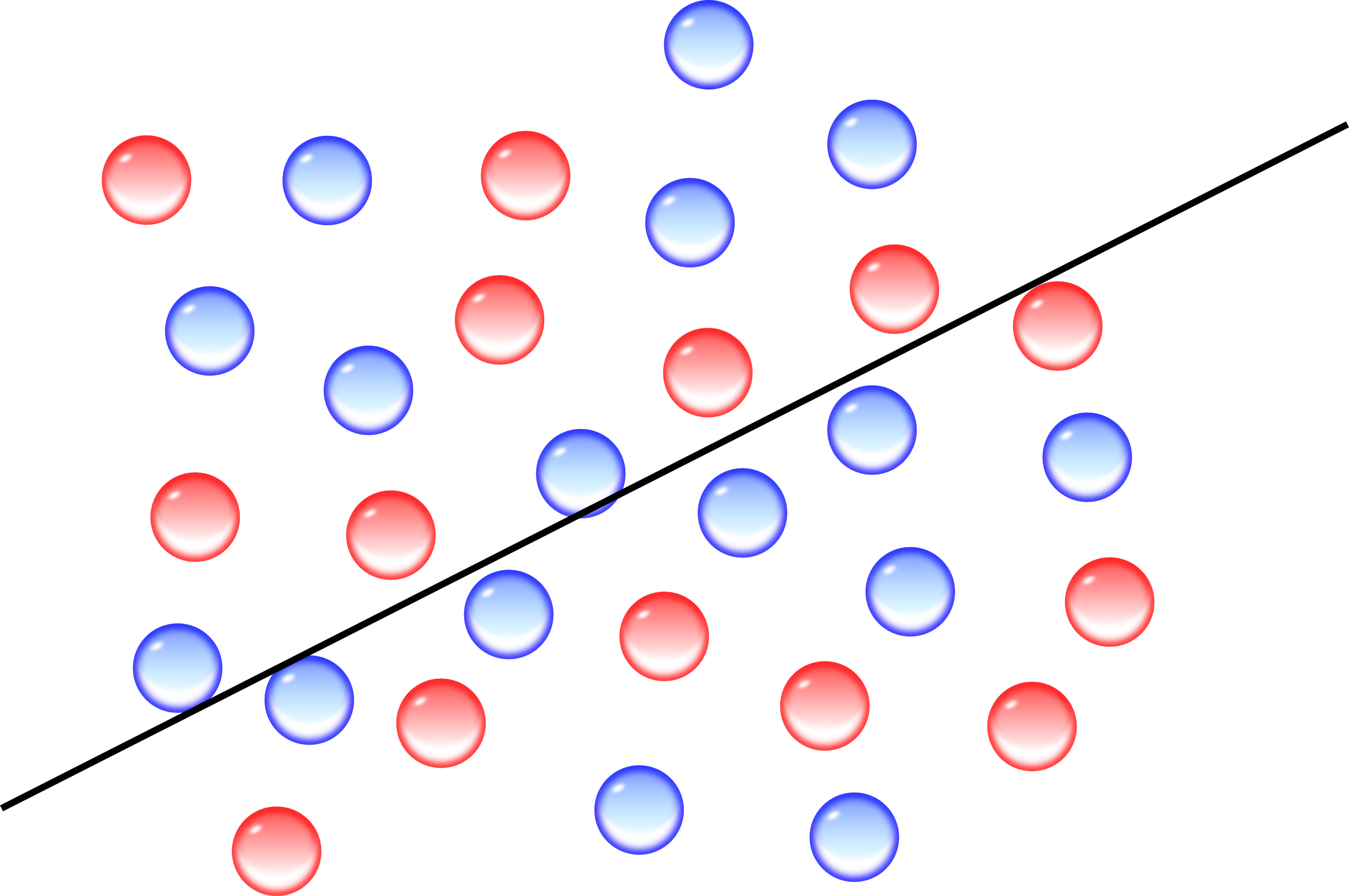
Timothy Gowers é provavelmente um dos maiores matemáticos vivos. Recentemente em seu blog, propôs uma explicação matemática para o problema americano de representatividade eleitoral; achei fascinante e decidi explorar um pouco essa ideia. Vamos falar hoje sobre eleições indiretas e sobre como posicionamento é, muitas vezes, mais relevante que números.

Os Estados Unidos possuem um sistema eleitoral indireto confuso o suficiente para merecer um diagrama da Folha de São Paulo a cada eleição americana. É um sistema a dois níveis com algumas sutilezas, cada estado tem seu peso, alguns estados decidem aplicar todo seu peso no candidato vencedor enquanto outros aplicam pesos proporcionalmente ao resultado de suas eleições. Veremos que ainda nesse caso a poucos níveis alguns problemas curiosos podem surgir.

Existem instituições com mais níveis de eleições indiretas, como, por exemplo, a Igreja Presbiteriana do Brasil. Nela, membros de uma igreja elegem alguns dentre si para serem os presbíteros, os presbíteros de várias igrejas se reúne; para eleger o supremo concílio e o supremo concílio elege seu presidente. Nessa lógica, há quatro níveis entre o presidente do supremo concílio e um membro da igreja. Esse método possui suas vantagens, a alternância de poder certamente é um antídoto ao culto à personalidade tão danoso ao proposto por muitas religiões; mas veremos que uma das consequências imediatas das eleições indiretas é a possibilidade de manipulação por posicionamento.

Vou usar um exemplo simples: o triunvirato. Imagine um país em que o presidente é eleito por três “sub-presidentes”, e precisa de dois dos três votos para ser eleito. Cada um dos sub-presidentes é eleito por três sub-sub-presidentes, e cada um precisa de dois dos três votos de seus sub-sub-presidentes para ser eleito. Imagine que isso acontece indefinidamente, até que toda a população foi contabilizada e contada nesse processo.

Para eleger o presidente que quero, preciso apenas ter na minha mão 2 dos 3 sub-presidentes, basta que eu eleja os sub-presidentes certos para realizar meu plano. E para eleger cada um deles, preciso ter sob minha influência 4 sub-sub-presidentes, dois para cada. É fácil perceber que em um sistema de $k$ níveis de eleições indiretas eu preciso apenas convencer um múltiplo de $2^k$ para meu projeto, enquanto a população, ao todo, é um múltiplo de $3^k$. Com alguns níveis, esses valores ficam completamente diferentes! Com dois níveis eu precisaria apenas de $\frac{4}{9}$ dos votos para eleger o presidente, menos da metade da população, sendo que eu estabeleci um critério mais exigente que o das eleições convencionais, exijo dois terços dos votos para eleger qualquer pessoa! Com quatro níveis, no caso da igreja, bastaria apenas $\frac{16}{81}\approx 20$% dos votos totais.

Esse sistema do triunvirato é familiar aos matemáticos, é conhecido como o conjunto de Cantor. Um dos melhores testes para um teorema em teoria da medida é aplicá-lo a um conjunto doentio e ver se ele ainda vale, e o de Cantor é o exemplo mais tradicional de quebra-teoremas nessa área. Para entender o que é esse conjunto de elementos, comece com o intervalo $[0,1]$ e tire o “terço médio”, ou seja, divida em três e tire o pedaço do meio. Com os pedaços que sobraram, divida cada um em três e tire o terço médio. Repita isso até cansar. Os elementos que sobrarem formarão o conjunto de Cantor:

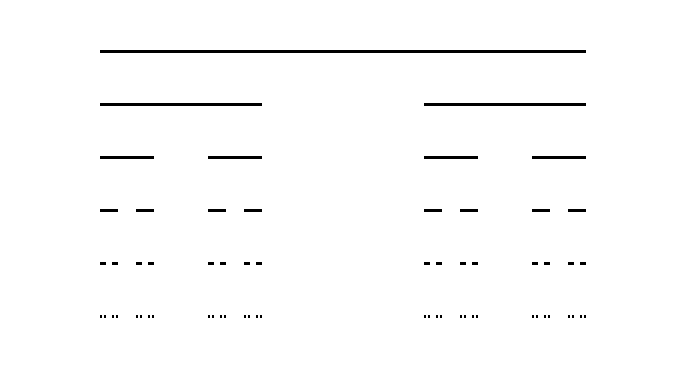É fácil ver que isso é exatamente nosso sistema de votação. A primeira barra é o presidente, a segunda são os sub-presidentes que devo convencer (o do meio posso ignorar, não preciso dele), a terceira são as pessoas que preciso convencer para que os de cima sejam eleitos. A quantidade de linha que resta é o quanto em população, proporcionalmente, preciso convencer para eleger o presidente. Quanto mais níveis de eleições indiretas, menos população eu preciso convencer. No conjunto de Cantor, a quantidade de linha que sobra é cada vez menor, dizemos que a medida do conjunto é nula quando o número $k$ é infinito.

Esse problema é mais grave do que se imagina. Se quiséssemos saber quantas pessoas teríamos que convencer para eleger o presidente, basta tomar a população total e ir subtraindo aqueles que não nos interessam. No primeiro nível, subtraímos logo $\frac{1}{3}$ do eleitorado, que votaria no vice-presidente que não nos interessa. Analisando as vice-presidências, poderíamos excluir $\frac{1}{3}$ de cada uma delas. Como cada uma delas já é $\frac{1}{3}$ do total, isso seria o equivalente a subtrair $\frac{2}{9}$. No próximo nível, é fácil ver que teríamos que subtrair $\frac{4}{27}$ da população. Ao todo, essa soma é:

\[ \frac{1}{3} + \frac{2}{9} + \frac{4}{27} + \cdots + \frac{2^n}{3^{n+1}} = 1 \]

A afirmação acima você pode verificar com sua fórmula favorita de somas de progressões geométricas infinitas. O resultado final é que teremos excluído todos os habitantes! Claro, isso é um absurdo decorrente de levar a soma ao infinito, de achar que há níveis infinitos de votações, o que isso realmente quer dizer é que aumentar o número de níveis do triunvirato significa se aproximar dessa realidade distópica em que uma minoria ínfima é capaz de eleger o presidente de uma democracia.

Os Estados Unidos são o exemplo mais gritante de práticas de “posicionamento” de eleitores para garantir a eleição indireta. Em nível regional, para as eleições de parlamentares, essa tática é chamada de Gerrymandering. A página da Wikipédia faz um bom trabalho na explicação, e as imagens são assustadoras: a redefinição de fronteiras para garantir um voto republicano ou democrata seria capaz de explicar a estabilidade de certos governantes; gente que pode quase levar o país à falência por um jogo político, com a garantia de reeleição porque o viés cultural de sua região é tão grande que não há o que temer.

Nós, contudo, temos o que temer. Diretas já não foi apenas um movimento social, foi também estatístico; representatividade indireta é sempre uma solução arriscada e falha quando o objetivo é transferir preferências pessoais a coletivas. Nos EUA, o resultado são os swing states, estados capazes de definir a eleição, ganhando por isso muito mais atenção na campanha política e deixando outros estados, incluindo Nova Iorque e Texas, órfãos de política nas presidenciais. A solução é simples: uma pessoa, um voto, e uma conscientização da população sobre o processo político. Contudo, esse blog nem sobre isso é, os fatores são muitos, a soma é quase infinita, mas acredito, de verdade, que converge.