Para o post de hoje, vamos ao México. Ele será um pouco mais sofisticado que meus posts habituais, mas acho que esse blog sentia falta de uma matemática um pouquinho mais pesada. Vou tentar manter Geek, sem passar ao Hardcore, prometo que, lendo com paciência, é um assunto fascinante.
A cidade de Cuernava, um pouco ao sul da Cidade do México, é um lugar muito especial para a física estatística e para quem gosta de matrizes aleatórias. Com um pouco mais que 300.000 habitantes, essa cidade apresenta um urbanismo estranho: ela é construída entre duas grandes rodovias que levam à capital do país e, entre elas, possui uma grande avenida central. Suas demais ruas, como os ramos de uma folha, se espalham entre as rodovias ao redor da avenida. Nessa avenida principal passa a linha 4 de ônibus de Cuernavaca, foco de nosso maior interesse, que possui propriedades fascinantes.
A linha 4 não é regulada por um sistema unificado de transportes, cada condutor de ônibus em Cuernavaca é dono de seu ônibus, como se fosse apenas um táxi grande, e quer, certamente maximizar seus lucros. Se, no entanto, dois ônibus estiverem muito próximos, o que está logo atrás sofrerá prejuízo financeiro; para evitar essa situação, os motoristas de Cuernavaca chegam a pagar “olheiros” posicionados estrategicamente na avenida para contar ao motoristas há quanto tempo o outro ônibus passou para que, assim, eles possam acelerar ou diminuir o passo, evitando encontrar o ônibus seguinte e o anterior. Diminuir a velocidade demais também não é bom pois, não apenas isso seria um serviço profundamente mal-prestado, mas ele correria o risco de ser ultrapassado pelo ônibus que o precede.
Dois físicos visitaram Cuernavaca em 2000 e ficaram fascinados com as características desse sistema de transporte. Durante um mês, eles coletaram dados de chegada e saída dos ônibus da estação central da linha 4 de Cuernavaca. Seus resultados foram relatados em um intrigante artigo, reproduzo o gráfico:
O valor que interessou os físicos foi: dada a chegada de um ônibus, quanto tempo o próximo demorava? Eles armazenaram esses dados em um belo histograma que, propriamente normalizado, resultou nos dados marcados com uma cruz no gráfico acima. As barras e a linha, que coincidem quase perfeitamente com os dados, são resultados teóricos de um modelo que os físicos suspeitaram ter a ver com o problema.
Se você tomar uma matriz hermitiana ($A=A^\dagger$) e colocar como entradas nela valores aleatórios tirados de uma distribuição gaussiana complexa, terá o que chamados de uma matriz do GUE, Gaussian Unitary Ensemble. Falei um pouco sobre matrizes gaussianas em um post anterior. Se as entradas da matriz são gaussianas, seus autovalores, como vocês devem suspeitar, possuem uma densidade de probabilidade bem diferente e, em particular, apresentam um fenômeno de repulsão logarítmica, ou seja, se os autovalores fossem partículas, elas se repeliriam com uma força que poderia ser interpretada como um potencial logarítmico na distância entre as partículas: $V(x) \propto \log|x_i-x_j|$. Em português, se você encontra um autovalor de uma matriz gaussiana em um ponto, é extremamente improvável encontrar outro muito perto dele. Se você estudar a estatística da distância entre os autovalores: tirar várias matrizes gaussianas aleatoriamente, diagonalizar, extrair autovalores, estudar a distância entre um autovalor e seu vizinho, fazer um histograma, normalizar corretamente e plotar em um gráfico, a teoria de matrizes aleatórias diz que você terá, quanto maior for a matriz, uma função cada vez mais próxima de $\frac{32}{\pi} s^2 e^{-4s^2/\pi}$.
Surpreendentemente, essa função é a linha plotada no gráfico acima, encaixando-se com perfeição nos dados. As barras são resultados de simulações feitas com matrizes gaussianas, colando mais uma vez com o resultado dos ônibus. O fato de os motoristas tomarem cuidado para não se aproximarem demais de seus vizinhos fazia o papel da repulsão logarítmica dos autovalores, e fazia com que os ônibus de Cuernavaca se comportassem como os autovalores de uma matriz gaussiana complexa.
O artigo segue com mais detalhes para comprovar seu argumento, mas aquilo não era o suficiente. Faltava criar um modelo para os ônibus que permitisse deduzir esse fato, que não é nada óbvio. Isso foi feito em um artigo seguinte, modelizando com carinho essa rede de transportes. Como queremos simplificar para compreender, o modelo pode não parecer muito realista; mas é isso que físico fazem: simplificam e tentam, na simplicidade, perceber a emergência de um fenômeno complexo e suas causas. Vamos aos ônibus.
Como o acelerar, desacelerar, parar, desabastecer-se e abastecer-se de passageiros é um processo complicado e imprevisível, precisamos simplificar drasticamente para que a matemática do modelo seja tratável. Ao invés de andar o caminho entre um ponto e outro, tomemos um modelo com duas hipóteses:
- Os ônibus ficam parados um tempo aleatório em cada ponto. Passado esse tempo, são “teleportados” ao próximo ponto.
- Dois ônibus jamais se encontram. Enquanto um está em um ponto, o próximo não pode teleportar a ele.
Com essas duas regras, podemos simular o comportamento desses ônibus em uma linha. Reproduzo o gráfico do artigo novamente:
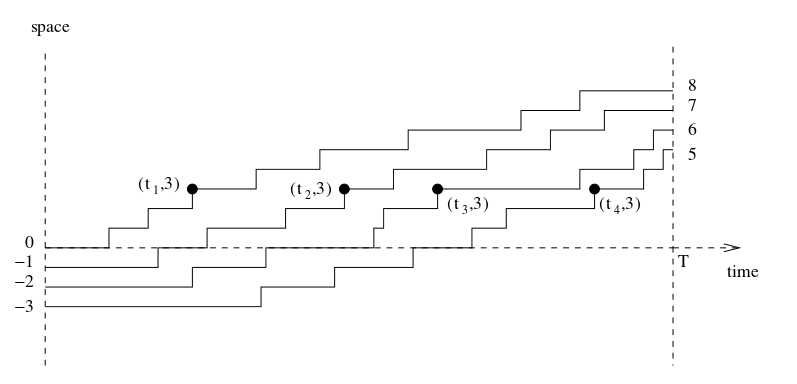Esse modelo, depois de algumas contas complicadas, nos conduz ao que queríamos provar: a distância entre os ônibus será dada pela mesma fórmula da distância entre valores próprios de uma matriz gaussiana. Claro, fizemos o modelo para que isso desse certo, e ficamos felizes que, apesar de simples, ele reproduz elementos importantes da realidade.
Não é um caso isolado. Os ônibus de Cuernavaca são um exemplo curioso e interessante do fenômeno de universalidade em matrizes aleatórias. Em uma analogia, é como se em sistemas complexos houvesse uma versão do teoria central do limite para processos altamente correlacionados. Não foi por acaso que Wigner, Dyson e Mehta escolheram matrizes aleatórias como tentativa de modelizar a interação forte no núcleo atômico, eles desconfiavam, com razão, que um processo estatístico acontecia em sistemas com um número suficientemente elevado de elementos. Tal processo, como toda boa estatística, mata as flutuações aberrantes e preserva as características extensivas do modelo.
Ainda não solucionamos o mistério da universalidade. A teoria de matrizes aleatórias aparece em contextos demais, não conseguimos ainda desvendar a razão disso. Em caos quântico há conjecturas fundamentais a respeito, em teoria dos números também. Essa emergência pode ser coincidência, ou pode ser manifestações de um teorema central do limite para variáveis fortemente acopladas. Não sabemos ainda, mas buscamos. Meu trabalho atual é um pouco sobre isso, estudar como é a transição de um sistema fortemente correlacionado, como os ônibus de Cuernavaca, a um sistema de variáveis independentes, como os ônibus de São Paulo. Essa mudança de comportamento é profundamente interessante, ocorre em diversos fenômenos físicos e é mediada pelas mais variadas formas de interação. Mas um novo post sobre meu trabalho fica para outro dia.
No grande tomo The Oxford Handbook of Random Matrix Theory, Freeman Dyson escreve no prefácio, após comentar sobre os ônibus de Cuernavaca:
“O benefício do sistema autorregulatório dos ônibus à população é medido pela variável $R$, a razão entre o tempo de espera médio de um passageiro e o tempo médio entre os ônibus. O melhor valor possível de $R$ é 0,5, quando a distância entre os ônibus é exatamente igual. Se os ônibus não são correlacionados, teremos $R=1$. Em Cuernavaca, como eles se comportam como autovalores de uma matriz gaussiana, temos $R=3\pi / 16=0.589$, muito mais perto da situação ideal que da situação independente. Não sou capaz de determinar se as aplicações de matrizes aleatórias no mercado financeiro, como as descritas no capítulo 40 deste livro por Bouchaud e Potters, geram algum benefício comparável. Quando um especialista em finanças me diz que algum pedaço de feitiçaria financeira certamente irá beneficiar a humanidade, sou levado a acreditar que um motorista de ônibus de Cuernavaca faria um trabalho melhor.”