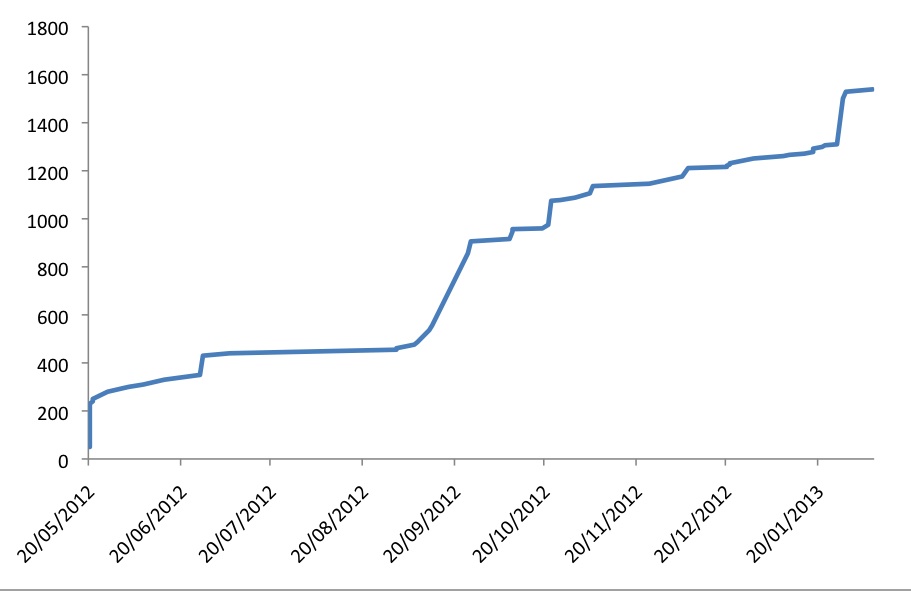
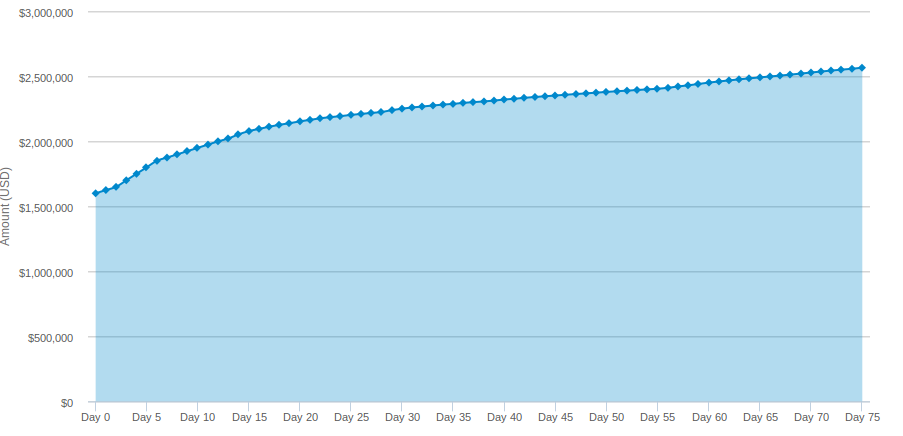
A quantidade de dinheiro envolvida em eventos esportivos sempre me assombrou. Ignorando a massa de recursos investida da estrutura e preparação de tais eventos, os prêmios em dinheiro aos que conseguem correr mais rápido, chutar mais certeiro ou apostar dinheiro de forma mais inteligente estão na casa dos milhões. A Forbes faz uma lista anual, sendo o décimo colocado o vencedor de quatro milhões de dólares. Essa lista, no entanto, está desatualizada; é preciso colocar um novo candidato: DotA, um jogo eletrônico, oferece em julho um prêmio de 5 milhões de dólares ao primeiro colocado, com 10 milhões ao todo a serem distribuídos aos primeiros lugares. Como é possível um videogame superar Cricket nessa lista? Ou, ainda, como é possível cada integrante do time vencedor de DotA receber mais que os jogadores de baseball vencedores da World Series? Esse prêmio, como muitos financiamentos dos últimos dois anos, não vem de uma única pessoa ou empresa; ele é resultado de um longo e extremamente bem elaborado crowdfunding, um projeto financiado por milhões de indivíduos.

Deixo de fora da discussão o aspecto econômico ou preditivo desse fenômeno, não me arrisco a escrever um daqueles artigos de “10 maneiras de fazer seu crowdfunding dar certo!”. Gosto dos gráficos e da evolução desses financiamentos. Vejamos alguns:

1. Stop/Eject, projeto de fotografia de Neil Oseman

2. Star Citizen

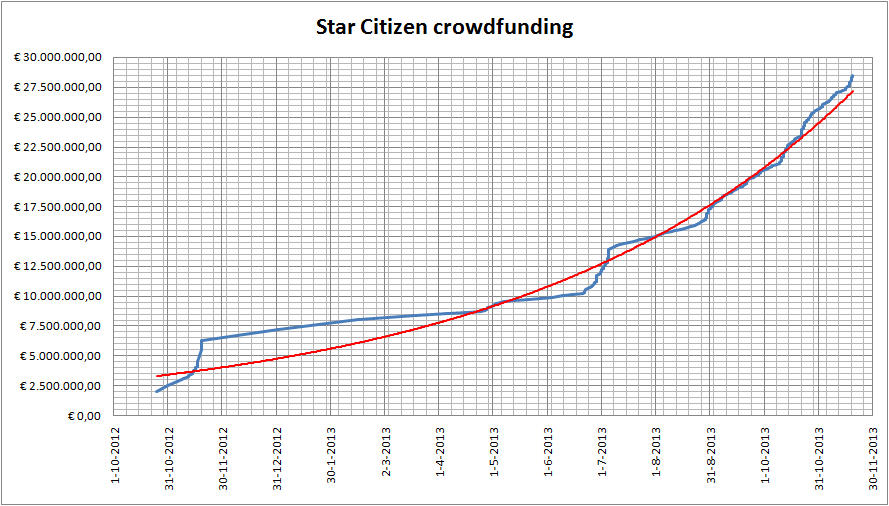Ignorem a linha vermelha, a azul é o financiamento!

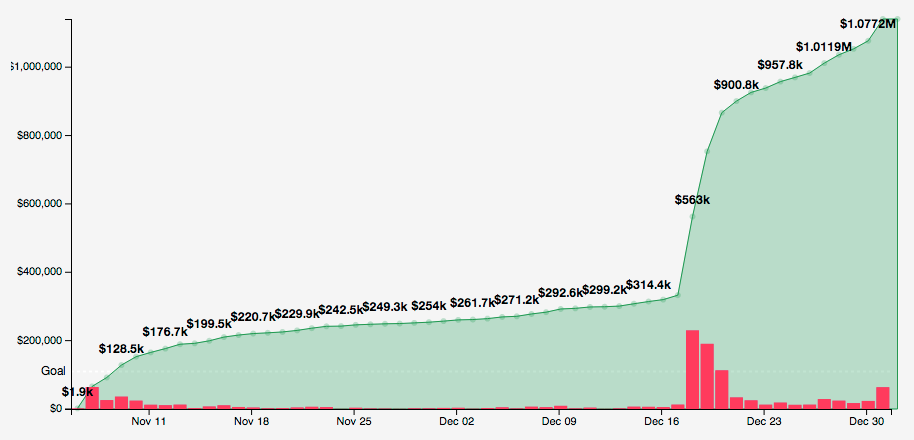
3. Dota 2, The International 2014

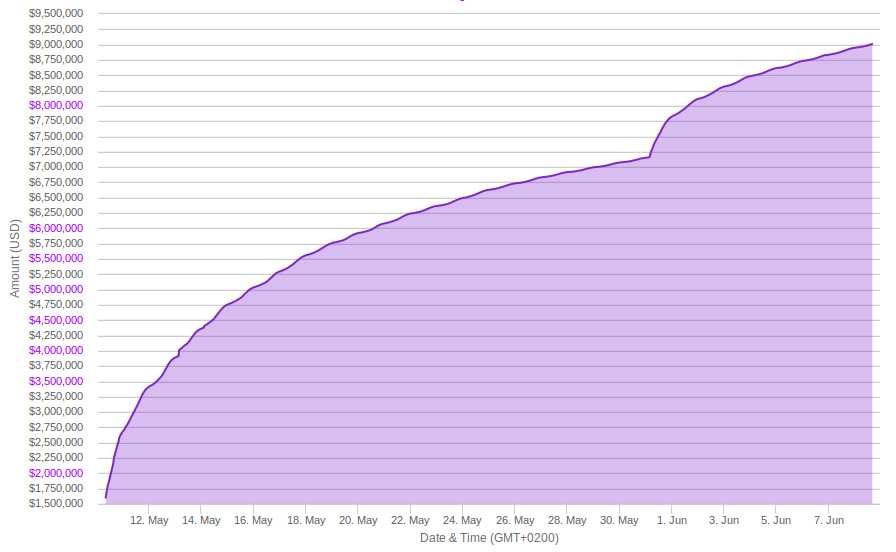4. Dota 2, The International 2013

5. Robot Dragonfly

Esses gráficos são bem diferentes e a esperança de explicar tudo com o mesmo modelo parece vã. Vou tentar construir um modelo matemático suficientemente simples para explicar a forma desses gráficos, e discutir os problemas do modelo. Vamos usar a técnica da teoria de cordas, criar uma teoria com tantos parâmetros livres que podemos plotar um coelhinho nos dados se quisermos.

Antes de continuar, precisamos combinar uma coisa. Todo modelo está errado, todo modelo é imperfeito e todo modelo é uma compromisso entre simplicidade e exatidão. Eu certamente deixarei de levar vários aspectos desse complicado fenômeno social em conta, e o trabalho do físico é exatamente esse: criar um modelo suficientemente simples para ser tratado e que considere os aspectos fundamentais do fenômeno.

O modelo que escolho para descrever crowdfunding é o modelo de Ising a temperatura nula. O nome é pomposo, mas o modelo é simples, levando em conta tanto a publicidade emitida pela fonte central do crowdfunding como a influência de seus amiguinhos para você dar ou não dinheiro ao projeto.

Nesse modelo, vamos construir uma rede quadrada de indivíduos, representando a sociedade alvo do crowdfunding. Cada pessoa é afetada por seus quatro vizinhos, seus amigos, da seguinte forma:

Cada indivíduo $i$ possui uma vontade de compra, um hype, representado pela letra $h_i$. Representamos cada indivíduo com uma coordenada $\sigma_i$, que vale zero se ele não contribuiu e 1 se contribuiu. Em meu modelo, se o hype é positivo, a pessoa contribui com o projeto. O hype é a soma de três fatores:

• Marketing da empresa e vantagens do produto, representados pela letra B.
• Influência dos amigos, representada pela letra $\sigma_i$.
• Resistência pessoal à compra, representada pela letra $R_i$.

Assim, o hype sentido por cada pessoa será \[ h_i = \sum_{i\sim j} \sigma_j +B – R_i,\] onde $i\sim j$ significa “$i$ é vizinho de $j$”.

O raciocínio é o seguinte. Cada pessoa apresenta uma resistência $R_i$, uma variável aleatória tirada de alguma distribuição. A empresa aplica um “campo de marketing” constante em todos, aumentando ligeiramente o hype. Algumas pessoas possuem o $R_i$ baixo, então contribuem com o projeto com pouco marketing. Essas pessoas influenciam as que estão a sua volta, que aumentam seu hype contribuindo com o projeto. Se a soma do marketing $B$ com a influência dos amigos for maior que a resistência $R_i$ à compra, ele é mais um que contribui com o projeto.

Esse tipo de cálculo é muito difícil de fazer na mão, melhor deixar a computadores. Vamos ver o que acontece em cada iteração desse sistema. Tomemos 10.000 voluntários em uma rede 100×100. Começamos com uma distribuição de rejeição uniforme entre 0 e 5. Coloquemos um marketing inicial de 0.25. Com isso, aproximadamente 5% dos indivíduos vão contribuir com o projeto apenas com o marketing inicial. Após esse surto inicial, outros serão convencidos pela presença de seus vizinhos. O resultado é o seguinte

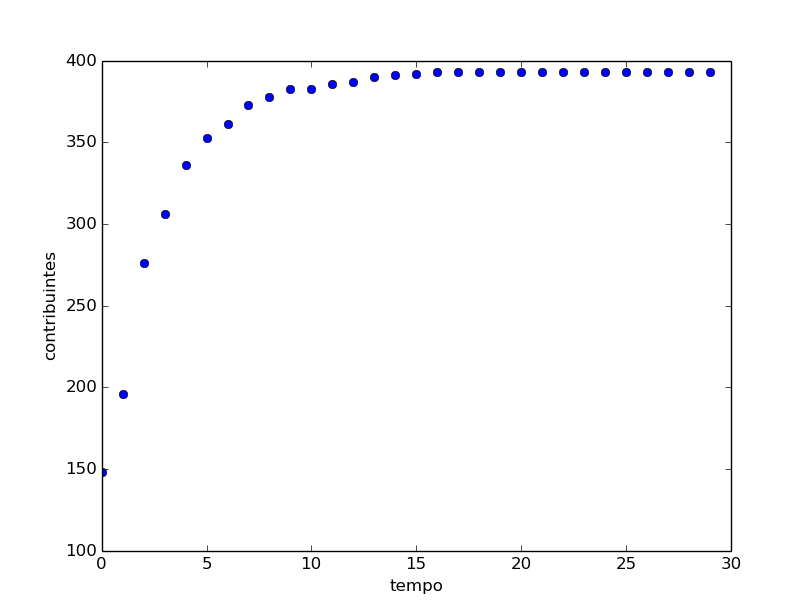Percebemos um crescimento inicial elevado seguido de saturação, o que é esperado. Você convence os amigos que pode até sobrarem apenas aqueles cuja rejeição é maior que o marketing aliado à influência dos amigos. Para conquistas mais adeptos, é necessário melhorar o produto ou o marketing. Vejam gráficos 3 e 5. Ambos representam drasticamente uma quebra no padrão, algo aconteceu nesses projetos. No primeiro, o campeonato de Dota, houve uma mudança na recompensa dada aos que contribuíram; em nosso modelo, isso significa um aumento de $B$. No Dragonfly houve uma divulgação em um jornal de grande porte, o que também é representado por um aumento de $B$. Vejamos o que acontece no gráfico anterior quando aplicamos $B=0.25$ até o instante 20 e passamos para $B=0.28$, um pouquinho mais elevado, após 20.

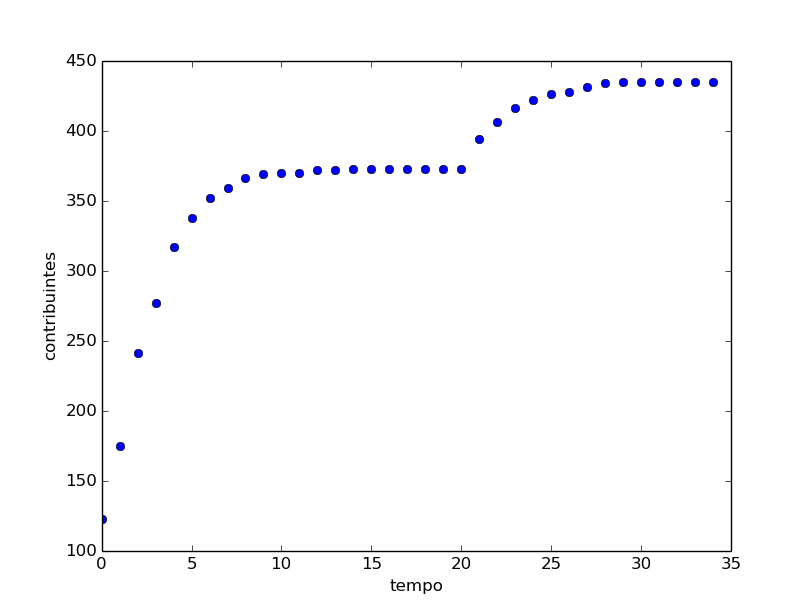E fico feliz, porque o modelo parece funcionar.

Como explicar os outros gráficos? Noto que essa estrutura de crescimento com saturação aparece em todos os exemplos, pequenos acréscimos no valor de $B$ são capazes de explicar as variadas curvas. Em outras palavras, com boa vontade podemos explicar todos os exemplos como “corcundas” e “saltinhos”; representados pela figura anterior.

E que resultados analíticos podemos extrair desse modelo? Infelizmente poucos, o modelo de Ising com entradas aleatórias é um monstro do ponto de vista matemático, algo perto do que chamamos de vidros de spin. Esse é um assunto sempre quente na física estatística, a quantidade de coisa para fazer é alta e a dificuldade dos problemas torna muitos problemas fáceis de explicar quase impossíveis de se resolver.

Percebemos uma saturação, queremos calcular o valor dessa saturação. Infelizmente essa resposta não é simples, veja o que acontece quando eu rodo meu código várias vezes, com as mesmas variáveis do primeiro gráfico.

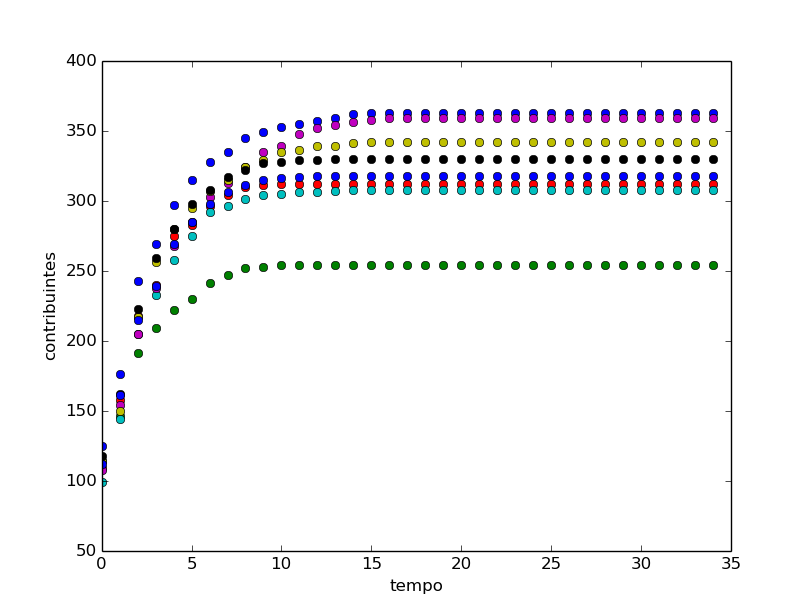Deu para perceber que a própria saturação é uma variável aleatória. A razão dessa grande diferença na saturação de contribuintes com os exatos mesmos parâmetros tem origem geométrica. Como eu atribuo uma rejeição aleatória uniforme nos indivíduos, eu corro o risco de criar “ilhas de rejeição”, regiões na grade 100×100 cercada por gente que não contribuiria com o projeto por nada nesse mundo. Essas pessoas, se unidas, podem impedir que indivíduos que com apenas um ou dois amigos entrariam na dança, mas, cercados de negatividade, decidem não o fazer.

É possível ao menos saber a média dessa variável? Honestamente, não sei, defiro a alguém que saiba mais de vidros de spin, não é minha área. Tentei uma abordagem de campo médio, mas minha resposta é quase o dobro do que acho numericamente, o que não de todo inesperado. A abordagem de campo médio é equivalente a considerar todo mundo conectado a todo mundo, enquanto aqui cada um é conectado a quatro. No campo médio eu driblo os problemas geométricos, as ilhas de rejeição, e percebo que elas são fundamentais para explicar os resultados.

Não tenho pretensões preditivas com esse modelo, foi só uma diversão de final de semana. Precisava colocar algum conteúdo desde que eu tomei férias após o último post sobre política, aquelas animações foram duras e a recepção de vocês fez valer a pena. Não sei se continuarei postando sobre política, posto o que achar interessante, talvez as eleições me animem. Por enquanto vou criando modelos para explicar gráficos bonitos, preenchendo com isso meus finais de semana. E, claro, com Dota.