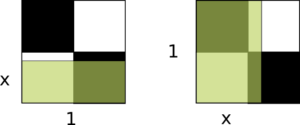Em meu post anterior, falei de retângulos inteiros e de um problema bonitinho relacionado. Nele, usei um truque sujo de livro de matemática para deixar a demonstração mais fluida e com aparência mas elegante, mas é como jogar a poeira para debaixo do tapete quando a visita vem em casa. Em um dos momentos mais importantes da demonstração, eu disse:
Tente desenhar um retângulo dentro de um quadrado 1×1 que cubra a mesma área de pretos e brancos. Sem muito esforço, você perceberá que só existem duas opções:
Não fui 100% honesto aqui. A afirmação é verdade, só existem aquelas duas opções, mas a parte do “sem muito esforço” é aquele velho truque do “é fácil ver”, “trivialmente”, “podemos mostrar que”. Eu não seria justo com vocês se não completasse essa parte, e faço isso nesse post. Isso é tanto por completude quanto por trauma, ainda lembro de passagens do Courant e Hilbert em que eu lia: “e nós podemos mostrar que“, mas no fundo entendia “e nós, e apenas nós, Courant e Hilbert, podemos mostrar que“.
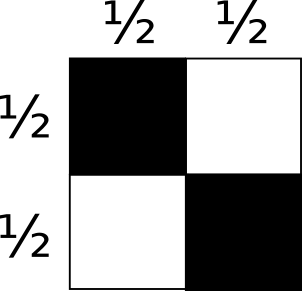
O que queremos provar é a frase: o único jeito de desenhar um retângulo que contém um vértice em $(0,0)$ de forma a cobrir a mesma área preta e branca na seguinte imagem:
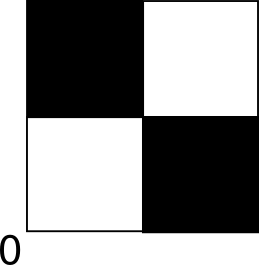é se um dos lados do retângulo for um dos lados da imagem.
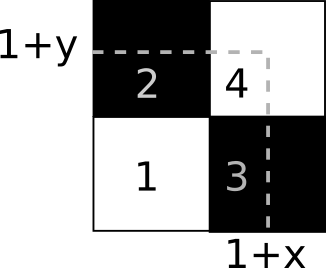
Para facilitar nossa vida, vamos mudar as dimensões do xadrez para que todos os quadrados pequenos tenham dimensões 1×1, o quadrado todo tem dimensões 2×2 agora. É fácil ver (e é realmente fácil ver dessa vez!) que se o retângulo começa em $(0,0)$ e está contido no xadrez, ele fica inteiro definido por um outro ponto que falta definir, o vértice oposto à origem (os outros dois vértices ficam obrigatoriamente nas arestas do xadrez).
Outro resultado realmente fácil de ver é que o único lugar em que esse retângulo tem chance de ter área preta igual à área branca é se o ponto que falta estiver nas bordas do xadrez (que são os casos que dissemos serem os únicos possíveis), ou no quadrante branco superior direito. Isso acontece por um motivo simples: o ponto que falta não pode estar no quadrante inferior branco, toda área seria branca. Ele também não pode estar em nenhum dos quadrados pretos, ele sempre pegaria área branca demais no caminho e só conseguiria compensar quando atingisse a borda (já cobrimos esse caso). Sobrou só o quadrante nordeste do xadrez, então colocamos nosso ponto lá. Já que ele sempre está no quadrante nordeste, vou parametrizar o ponto com $(1+x, 1+y)$, porque assim as contas ficam mais fáceis.
É aí que as coisas ficam interessantes. A área branca será a soma de toda a área do quadrante branco inferior (1) com a pequena área que o retângulo ganha no quadrante superior (4). A área preta é a soma das áreas dos retângulos formados acima (2) e à direita (3) do grande quadrado branco. Como os retângulos pretos são maiores que o pequeno branco e menores que o grande branco há, em teoria, a chance de juntando suas forças eles igualarem os brancos! Essa é uma possibilidade real e o único empecilho ao meu “sem muito esforço” do post anterior, eu preciso provar que a área de (1) + (4) nunca é igual à de (2) + (3).
Vamos calcular essas áreas. (1) tem sempre área $1$ (lembre que eu mudei a escala do xadrez). (2) tem área $y$ enquanto (3) tem área $x$. (4) tem área $xy$, e meu objetivo é provar que, se $0 < x , y < 1$, então
\[ 1 + xy \neq x + y. \]
Provar isso é simples, já que:
\[\Rightarrow 1 + xy-x-y \neq 0 \]
\[ \Rightarrow (1-x)(1-y) \neq 0, \]
o que de fato é verdade se $x$ e $y$ estão entre zero e um, com a igualdade se verificando quando um deles é igual a 1.
Isso termina a demonstração ((Eu sempre achei que um autor que tem que avisar quando a demonstração acaba é como um comediante que tem que avisar quando a piada acaba. “Isso termina a piada.”)), bonitinha e elegante. Mas tenho algumas opiniões fortes para terminar esse post.
A primeira é a linha tênue entre coisas que precisamos ou não demonstrar, do quão subjetivo é esse “sem muito esforço”. Perdemos bem rápido a empatia com nosso estado anterior de quem não sabia um assunto, isso é especialmente verdade depois de ver muita matemática. Alguns conceitos de base são desafiadores a explicar depois de muita exposição às exatas, eu arrisco dizer que o Ricardo de 15 anos explicaria melhor a seu colega por que $2x + 1 = y$ é uma reta do que o Ricardo de 29 anos. Contudo, isso não justifica minha mão leve na demonstração anterior; fosse isso questão de prova, eu tinha obrigação de demonstrar. Não sou desses de deixar demonstração para o leitor, quem sabe faz ao vivo.
A segunda foi meu instinto inicial para provar que $1 + xy-x-y \neq 0$ na parte interna do quadrado $0 < x,y < 1$. Eu estava sem lápis e papel quando cheguei nessa parte, a transformação, que é absolutamente simples, não me veio imediatamente. O que me veio foi: Ah, $f(x,y) = 1 + xy-x-y$ é solução da equação de Laplace, então não tem máximo ou mínimo em domínio aberto, só na borda. Nas bordas essa função é ou zero, ou $1-x$, ou $1-y$, então tranquilo, zero é mínimo e só é atingido naquela borda.
Essa aberração de demonstração vem de outra tendência minha: se há duas maneiras de resolver uma questão, eu necessariamente escolho a mais difícil. Sou aquele tipo de pessoa que, se preciso provar que $\sqrt[3]{2}$ é irracional, provaria da seguinte forma:
Suponhamos, por absurdo, que seja racional; ou seja, que existam inteiros $p$ e $q$ tais que $\sqrt[3]{2} = \frac{p}{q}$. Elevamos os dois lados ao cubo, temos que $2 = \frac{p^3}{q^3}$. Passando para o outro lado, como se deve, temos que $2q^3 = p^3$, ou seja, que $q^3 + q^3 = p^3$. Contudo, pelo último teorema de Fermat, isso não é possível, então $\sqrt[3]{2}$ é irracional.
É triste que essa demonstração não seja robusta o suficiente para provar que $\sqrt{2}$ é irracional. Pior que isso, não garanto que Wiles, em sua demonstração, não use o fato de que $\sqrt[3]{2}$ é irracional para provar o teorema, o que traria todos os problemas tautológicos dessa abominação de demonstração, que é uma de minhas favoritas.
