Arquivo da tag: Física Estatística

Posts sobre física-estatística e matéria condensada.

Meu trabalho

Hardcore Rookie

Tirei férias, viajei a trabalho e abandonei o blog, confesso. Peço desculpas pela ausência de aviso, já que avisei ano passado, mas até durante a viagem esqueci meu carregador e meu notebook era apenas um peso de papel tecnologicamente avançado. Nesse último mês, coloquei meu primeiro artigo no arXiv, um grande site que abriga artigos científicos e os disponibiliza gratuitamente. Você pode conferir meu trabalho aqui, mas dificilmente ele será muito compreensível, então aproveito esse post para me fazer entender, e tentar explicar o que foi meu trabalho desses últimos meses.

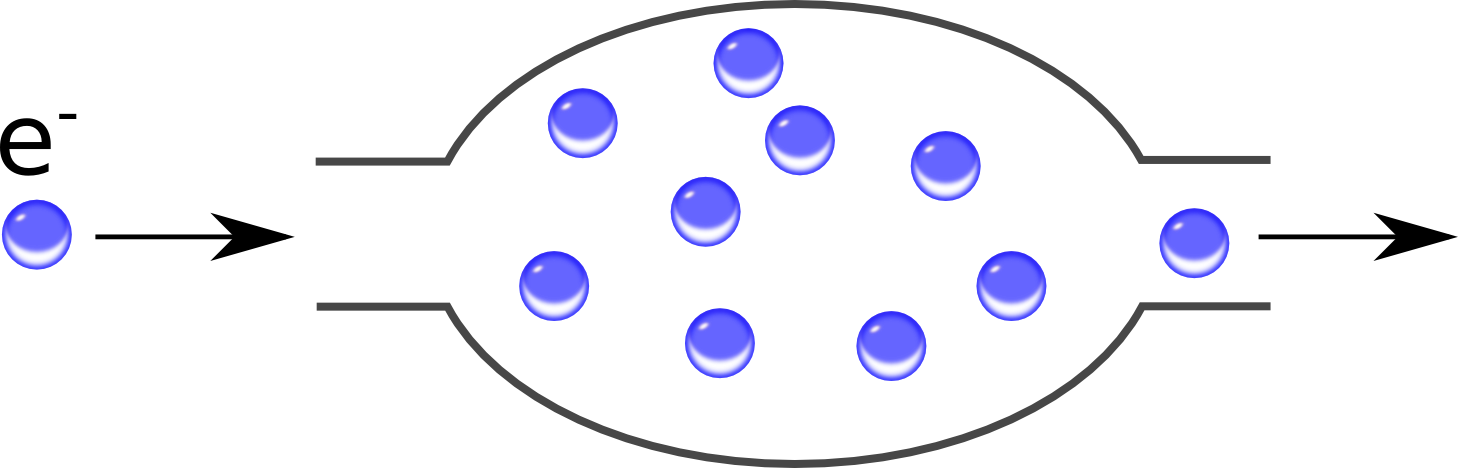
Transporte de elétrons é algo bem importante na física, compreender e dominar essa arte é fundamental para construir qualquer aparelho eletrônico que se preze. Não domino nada de eletrônica, mas gosto de elétrons, e imagino um sistema da seguinte forma: elétrons podem entrar em uma “caixa” com propriedades praticamente desconhecidas, e podem sair dela. Dentro, fazem o que quiserem, e eu tenho pouquíssimo controle do que acontece nessa caixa. A pergunta é: sem saber praticamente nada sobre essa caixa, qual a melhor estimativa que posso fazer do fluxo de elétrons nesse sistema?

quantum_dot_1

Eu honestamente prefiro elétrons em amarelo, mas em azul fica mais fácil ver, e é a preferência da física de partículas com que divido o apartamento. Essa pergunta sobre o fluxo de elétrons não é fácil, e é importante, esse tipo de sistema existe na vida real e a eletrônica de seu celular é cheia deles. Conhecido como “ponto quântico”, quantum dot, esse é um dos modelos mais simples de transmissão de elétrons em meios desconhecidos. Na vida real, isso é mais próximo dessa imagem:

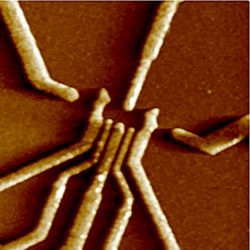quantumdot Essa questão vem sendo respondida desde os anos 80, sempre com um modelo “ideal” em mente. Neste modelo, a caixa e os conectores são perfeitamente acoplados, não há chance de um elétron não entrar ou de não sair, ou seja, não há reflexão de elétrons no contato entre a caixa e os conectores. Esse modelo é extremamente bem sucedido, mas longe da realidade, e meu artigo é sobre aproximar esse modelo da realidade.

Em 2007, Kanzieper e Vidal deduziram como é esse fluxo para o caso em que há impurezas entre os conectores e a caixa. A fórmula que eles obtiveram é horrível, impraticável, ainda que não exatamente feia. Tanto é difícil que os autores só conseguiram estudar o caso de conectores muito pequenos, deixando passar apenas elétrons em uma dada velocidade, um modelo bem limitado. Nesses últimos quatro meses, tratei essa fórmula com muito carinho, e consegui resultados para um modelo um pouco diferente: podemos agora deixar passar quantos elétrons quisermos, e podemos calcular esse fluxo em qualquer precisão, mas minhas fórmulas funcionam melhor para pequenas impurezas. Quanto maiores as impurezas, mais conta você vai ter que fazer. Não é um modelo ruim, porque em geral o número de impurezas é pequeno. Ora, se o caso ideal já era bem sucedido, o caso “impurezas pequenas” será ainda melhor.

E esse foi meu trabalho. Não parece muito emocionante, não parece explicar a origem dos átomos, ou não revela uma verdade fundamental da natureza, mas isso é fazer ciência. O que aprendemos na escola, e a maior parte do que você encontra por aí, é ciência pronta, tudo acabado, bonitinho, ciência que já tem décadas, ou séculos, de idade. Fazer ciência, ser cientista, é como abrir caminho na floresta com um facão, não sabemos o que vamos encontrar, é difícil atravessar obstáculos e podemos muito bem não chegar a lugar nenhum. Se encontramos, no entanto, uma descoberta fascinante; logo esse caminho será alargado, asfaltado, iluminado e a descoberta receberá o tratamento que merece, só então ela vai parar nas escolas ou na divulgação científica.

A partir daqui, o post se torna Hardcore. Continue por sua conta em risco.

Eu não poderia encerrar esse post sem comentar algumas coisas específicas do meu artigo. Como vocês são gente grande na ciência, posso colocar uma imagem mais adequada do quantum dot:

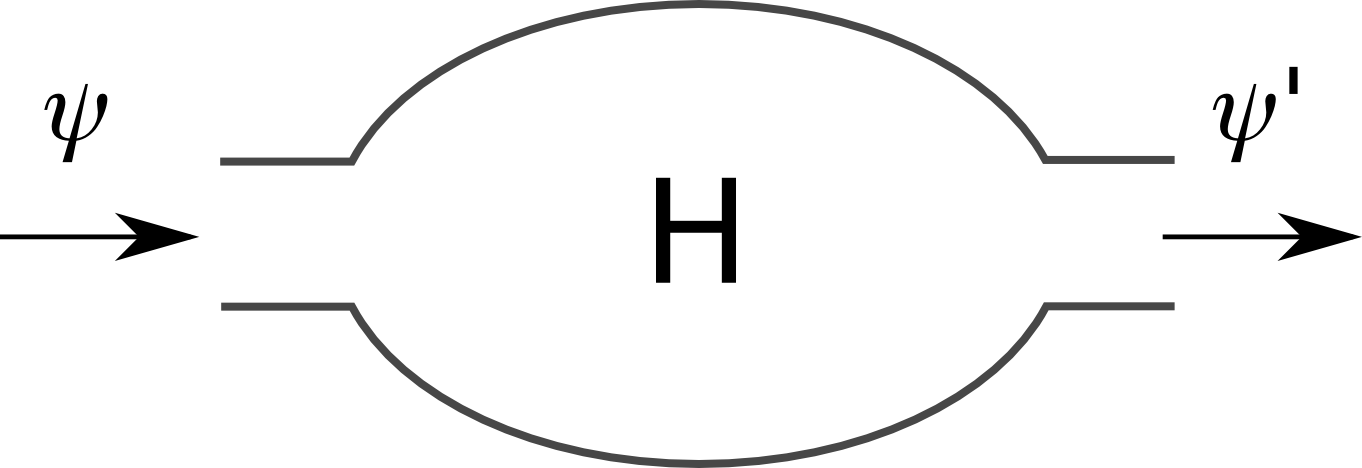quantum_dot_2Temos uma função de onda dos elétrons que entra e uma que sai. Os conectores desse tipo de sistema costumam ser projetados para deixarem passar funções de onda com um número de onda específico, ou seja, se decompusermos $\Psi$ em ondas planas, o conector vai transmitir apenas $N$ modos de onda. Analogamente, o conector de saída pode deixar passar $M$ modos. Esses valores são importantes, pois se são muito grandes a onda passa praticamente inteira.

A caixa sendo desconhecida, uma maneira de tratar o problema é supor que os elétrons sofrem espalhamento quântico no interior. Sendo agora um problema de scattering, podemos deduzir a matriz $S$ do problema (a matriz que torna a função de onda inicial na final: $\Psi^\prime=S\Psi$). O problema é que, para haver a $S$, precisamos no hamiltoniano da caixa, $H$. É um pouco complicado, mas possível, deduzir que, se a caixa é desconhecida, o hamiltoniano que maximiza a entropia e representa nossa melhor estimativa é um cujas entradas são gaussianas.

Um hamiltoniano gaussiano gera uma matriz $S$ do tipo “Poisson”, que é uma matriz complicada. Se supusermos o caso ideal, apenas o hamiltoniano da caixa conta e não há hamiltoniano de acoplamento entre a caixa e os conectores, então essa matriz $S$ será uma matriz uniformemente distribuída no espaço das matrizes unitárias. A partir dela, podemos estudar o que chamamos de autovalores de transmissão, que são os autovalores da parte de transmissão da matriz $S$. O trabalho de Kanzieper e Vidal deduz a densidade de probabilidade para esses autovalores, mas essa p.d.f. é horrenda. Neste artigo, descobrimos que se essa p.d.f. for expressa em termos de polinômios de Schur, ela fica muito mais bonita, e, além disso, podemos expressar a probabilidade do caso não-ideal como a do caso ideal vezes um fator de correção. Ele é feio, é verdade, mas essa informação é fundamental, porque podemos importar todos os cálculos de momentos e probabilidades do caso ideal (estudado desde os anos 80) para o não-ideal, bastando apenas multiplicar pelos fatores adequados. Se esse assunto interessar alguém, recomendo a excelente review de Beenakker.

1 resposta

A vontade dos átomos

Rookie

Eu gostava de botânica no colégio, não sei exatamente a razão, e muitos professores tentaram me convencer a não gostar. Quando tive uma vez, em um exercício, que ordenar alguns seres vivos em escala evolutiva, coloquei a árvore em primeiro lugar, seguida do homem e do resto. Perdi pontos, fui reclamar, a professora ficou espantada com a resposta, não entendia como eu podia achar um organismo sem sistema nervoso, sem quase sistema nenhum, aliás, mais evoluído que o ser humano; e eu não conseguia entender como ela não percebia que a fotossíntese, sozinha, era mais impressionante que tudo isso.

Ainda que ela tivesse razão, plantas não possuem quase nenhum sistema, eu argumentei que elas não precisavam dessa parafernalha toda, desses adendos que criamos porque não somos capaz de transformar luz em matéria. Ainda, um detalhe nunca me convenceu: nessa ausência de sistemas, como as árvores carregam água e sais para o topo de suas copas sem qualquer sistema circulatório? Seiva e sangue me eram parecidos demais, mas a seiva parecia subir dezenas de metros magicamente, enquanto nós empurramos o sangue nos poucos metros que temos a pesadas bombeadas. Quando, no cursinho, dei vazão a essa inquietude, a resposta veio da professora de biologia: quem carrega nutrientes para o topo das árvores são a osmose e a difusão; mas isso não é resposta, é apenas um nome. A professora explicava osmose como “a tendência da água a ir do meio menos concentrado ao mais concentrado em soluto”, mas o que era isso? Ela explicava como se a molécula de água quisesse se afastar de suas companheiras, como se átomos tivessem vontade, deu-nos até uma analogia de que, em um ônibus, você sempre busca o lado mais vazio para ficar. Átomos nada querem, nada pensam e não usam transporte público, aquilo não me convencia.

E quando reclamei que aquilo não colava, que não fazia sentido, ela desdenhou. Disse que se eu não entendia aquilo, como pretendia ser físico? Calei-me com o orgulho ferido, mas hoje penso que deveria ter insistido. Era exatamente porque queria ser físico que exigia uma resposta em termos científicos, ela me respondia quase como Aristóteles, que insistia em argumentar no cansaço dos corpos durante o movimento para justificar por que um objeto desacelera enquanto anda. Hoje penso que uma resposta mais refinada ela provavelmente não tinha, esta me veio apenas muito depois, entre um curso e outro de física estatística.

Ademais, osmose não é a razão da subida da água nas árvores! As plantas são capazes de criar uma grande diferença de pressão através da evaporação, como uma bomba de água em escala microscópica, algo muito impressionante. Esse vídeo explica a questão de maneira muito linda. No seguinte do post, comento sobre a osmose. O caso da árvore não é o melhor, então esqueçamos esse exemplo por enquanto e falemos apenas em soluto andando pela água, ou da água andando de um meio a outro.

É verdade que essa parece ser a tendência da água, e de várias outras coisas. Óleo também gosta de ir do meio com muito óleo para um de pouco óleo, sódio e potássio vivem brigando para se equilibrarem em proporções em nosso cérebro, tudo o que não é sólido costuma apresentar esse comportamento. Aprendemos isso no colégio com os nomes de osmose e difusão, mas, se quer saber, acho que o conceito é mais simples que os nomes. O que não nos contam é que átomos, moléculas, gases e líquidos não querem ir para uma direção, ele vão para todas as direções possíveis, aleatoriamente. Mas, de nosso ponto de vista, parece que estão indo para uma direção específica.

Isso não é tão simples de entender. Para explicar, vou representar com alguns desenhos que deram bastante trabalho para fazer. Como eles são bem pesados, vou apenas colocar o link aqui, se eu os mostrasse na mesma página do post, não há browser que aguente.

Imagine um sistema com água de um lado e outro produto, em vermelho, de outro lado. O que vemos, de nosso ponto de vista, é uma imagem parecida com isso:

IMAGEM

O que certamente parece magia, o produto, que chamamos de soluto, sobe a coluna contrariando a gravidade. A animação é um pouco lenta, confesso, mas tenho que zelar pelo processamento de seus computadores. O que aprendemos na escola é isso: o soluto “quer” ir do meio “hipersoluto” para o meio “hiposoluto”, o vermelho que ir do meio “hipervermelho” ao “hipovermelho”, do muito vermelho ao pouco, como se quisesse se afastar de seus colegas.

Isso não poderia estar mais longe de uma explicação mal dada. O que esquecem de nos avisar no colégio é que há muito mais no meio em que a difusão acontece que apenas as bolinhas que se difundem! Faltou, por exemplo, incluir a água nessa história, e talvez o comportamento das bolinhas fique mais claro nessa nova imagem:

NOVA IMAGEM

O soluto não escala ou não invade nenhum território porque quer, pois nada querem, nada desejam, eles apenas vão para todos os lados, mas a água também vai para todos os lados! A tendência natural das coisas é, depois de tempo o suficiente, estarem completamente misturadas, não porque elas querem ir de onde há muito para onde há pouco, mas porque isso é o estatisticamente mais provável. Nessas simulações, eu apenas inseri as fórmulas matemáticas para a resolução de um problema de colisão de duas partículas e deixei rodar. Foi razoavelmente difícil, e eu poderia ter ainda otimizado mais, mas o resultado ficou bonito, fiquei orgulhoso.

E isso explica a vontade dos átomos. Eles não querem, vão para todos os lados, mas, por um fenômeno estatístico, dão a impressão de se deslocarem de onde há mais átomos para onde há menos. Os vermelhos parecem subir e os azuis parecem descer, é verdade, mas isso esconde o fato de que há também azuis subindo e há também vermelhos descendo. Ao final do dia, teremos um sistema completamente misturado.

A difusão e a osmose ocorrem na planta, claro, e é dessa maneira que os nutrientes se espalham pela seiva, mas a razão da subida da seiva não é osmose, é mais complexa. A difusão dos nutrientes pela água, que, essa sim, é sugada pelo tronco, isso é certamente difusão. Os nutrientes não escolhem se espalhar pela água, não decidem ocupar regiões de poucos nutrientes como pessoas ocupam lugares vazios no ônibus, eles apenas vão para todos os lados e, conforme a água é sugada pelo tronco, acompanham esse movimento.

Se você achou a simulação muito lenta, essa era minha intenção, a difusão é um processo bem lento. Pretendo em seguida usar essas simulações para explicar mais coisas sobre os átomos, elas deram muito trabalho e pretendo capitalizar nesse algorítmo. Enquanto isso, divirtam-se com esse hipnotizante balé dos átomos, acompanhando um deles na aventura, divertindo-se enquanto ele, indo para todos os lados, encontra outros, rebate, sobe e desce, ainda que contra sua vontade.

Bonus Round: Se você gostou das animações, brinque com elas. Usando o mouse, você pode empurrar bolinhas e, em uma linguagem física adequada, acelerando uma, você aumenta a temperatura de todo o sistema!

9 respostas

Branco como a neve

Rookie

No natal de 2010, fui esquiar pela primeira vez. Como brasileiro, havia visto neve havia pouco e já achava impressionante, e um pouco irritante. Neve é molhada, fria, incômoda, mas linda, de um branco puro que torna qualquer paisagem um filme da Disney. No esqui, descobri um outro lado dessa pureza branca, em pouco mais de duas horas na montanha meus olhos começaram a doer, arder, como se eu tivesse jogado videogame durante dez horas. Eu estava sem óculos de proteção porque não estava nevando, mas eu não sabia que o óculos não servia apenas para proteger dos flocos, o que atacava meus olhos era o branco da neve.

A exposição continuada a branco por todos os lados, céu, casas, chão; a reflexão de luz solar em grande intensidade por todas as superfícies estava fazendo meus olhos arderem. Perguntei-me, então, o que torna a neve tão branca? Por que nem a chuva, nem o gelo são de um branco tão puro, se são quase a mesma coisa? A resposta está na natureza do branco, da luz, da neve e em um álbum do Pink Floyd.

A luz é uma onda eletromagnética, mas isso não quer dizer muita coisa para quem não é do ramo. Na natureza existem dois campos: o elétrico e o magnético. Um campo é uma ideia física usada para entender a “influência” que uma partícula carregada exerce em outras. Se colocamos uma partícula carregada em um ponto e a deixamos parada, basta colocar outra perto para perceber que essa outra irá se mexer, ser atraída ou repelida pela primeira, dependendo de sua carga. E podemos trocar a posição dessa segunda carga e perceber que essa atração ou repulsão vai mudar bastante de acordo com o lugar que escolhemos. Vamos além, dizemos que a primeira carga gera um campo elétrico em torno de si, uma influência que, a cada ponto, fará a tal segunda partícula andar para uma direção. Ficou claro? Um desenho sempre ajuda:

Nesse desenho, as linhas indicam para onde uma outra carga positiva iria se colocada lá. E essas linhas é o que chamamos de campo elétrico, a influência da carga azul sobre o meio que a cerca.

Essa ideia é muito mais que uma abstração para ajudar a entender o eletromagnetismo. O campo elétrico é algo real, tanto quanto as cargas e as partículas, ele pode ser medido, absorvido, pode se mover e obedece a equações muito precisas, chamadas Equações de Maxwell, talvez a jóia da física clássica. Essas equações predizem também o campo magnético, que é muito parecido com o elétrico, mas afeta cargas em movimento. Há muita física séria envolvida nesses dois campos e em suas relações e origens, mas o que quero passar para vocês hoje é: existem, são dois e um vive em função do outro, não existem separadamente.

As equações de Maxwell nos dizem que uma variação no campo elétrico causa uma variação no magnético e vice-e-versa. Esse balé entre os campos é o responsável pela geração de toda energia elétrica que está à disposição em sua tomada, mas isso é assunto para outro post. Essa influência mútua gera um fenômeno fascinante: imagine-se dando, por um momento, um “tapa” no campo elétrico. Ele aumenta, o que fará o campo magnético também se mexer, ele, que era zero, aumentará em uma direção. O magnético mudando, o elétrico também será afetado, e começará a diminuir, o que, por sua vez, fará o magnético diminuir. Como um carro que de tanto dar ré acaba voltando ao ponto de partida e correndo para a direção contrária, o campo elétrico continua crescendo, mas para o lado oposto, o que também arrastará o magnético para o lado oposto de sua direção inicial. A descrição parece confusa, por isso vou tentar com outra imagem, tirada daqui, um blog de divulgação de nossos amigos gregos:

Para entender esse aumenta e diminui dos campos, fixe o olhar em um ponto dessa linha na base das flechas. Para esse ponto, os campos aumentam e diminuem constantemente. Essa dança entre os dois campos se propaga no espaço indefinidamente, até atingir algum objeto. Os físicos chamam esse fenômeno de propagação de uma onda eletromagnética, mas você deve conhecê-lo pelo nome luz.

Digamos que o vermelho seja o campo elétrico e o azul, o magnético. Se você está parado em um ponto dessa linha, como uma bóia sente as ondas do mar subindo e descendo, você sentirá o campo magnético aumentar, diminuir, mudar de direção, aumentar e diminuir. Esse processo ocorre a uma frequência, o campo elétrico vai e vem algumas vezes por segundo. Se ele ocorre entre 400 e 800 trilhões de vezes por segundo, seu olho consegue detectar essa onda, e você a interpreta como cores.

E isso é enxergar: ser capaz de absorver um campo elétrico oscilando a uma taxa entre 400 e 800 trilhões de vezes por segundo. Se ele oscila mais perto dos 400, ele campo elétrico será interpretado como a cor vermelha. Se mais perto do 800, será mais perto do violeta. As outras frequências intermediárias serão todas as cores do arco-íris.

Mas seu olho possui um comportamento ainda mais complexo que o de um simples detetor. Se ele recebe muitas ondas eletromagnéticas de diferentes frequências juntas, não é capaz de diferenciar uma por uma, ele interpreta essa mistura de ondas visíveis como uma nova cor, que não existe como cor pura. É dessa maneira que o rosa, o cinza, o bege e, em particular, o branco surgem, afinal, eles não estão no arco-íris, devem surgir de algum lugar.

A água, por razões muito interessantes, que não cabem nesse post (talvez em outro), é transparente. Mas assim como o vidro, ela é capaz de causar a difração da luz. A luz branca é feita de ondas de diversas frequências, e essa onda, dependendo de sua frequência, inclina mais ou menos quando atinge o vidro. O que acontece é o fenômeno dessa figura:

A luz branca, atingindo o prisma, se decompõe. Leis do eletromagnetismo nos explicam esse fenômeno, o ângulo de inclinação de um feixe luminoso dependerá de sua frequência, pouco, mas dependerá, e é isso que vemos.

O prisma de vidro é extremamente regular, bem como a água líquida, e por isso eles são transparentes e, no máximo, afetam a luz branca com uma pequena difração. Se colocarmos muitos prismas juntos, esse efeito se acumulará, um rebaterá a luz em outro que rebaterá no próximo, logo perderemos o controle de qual luz vai para onde. Um conjunto muito grande de prismas emitirá, praticamente, para todos os lados, luz branca (uma mistura caótica de todas as frequências que os prismas bagunçaram). Quando nosso olho recebe essa quantidade alta de ondas eletromagnéticas em tantas frequências, interpreta esse material como de uma cor branca muito pura.

A neve é apenas isso, pequenos pedaços de água solidificada que funcionam como os prismas de Pink Floyd. É pelo fato de ser um conjunto tão caótico e desorganizado de “prismas” que a neve é tão branca, tão pura e tão homogênea. Curiosamente, a desorganização completa é responsável pela homogeneidade, porque, sendo caótica, ela não privilegia lado nenhum, frequência nenhuma e emite apenas branco para todos os lados. Esse é o mesmo princípio do filtro solar, que, em uma explicação grosseira, é equivalente a uma pasta de vidro moído.

E quando meus olhos receberam aquela quantidade tão grande de branco por todos os lados, refrações e reflexões de tantos cristais que caíram do céu, não deveria ter me assustado o cansaço que me atingiu. E não apenas neles, o cansaço das quedas na neve, e cansaço de ver crianças de cinco anos deslizando sobre esquis com leveza, o frio cortante da neve que havia entrado em minha roupa em algumas das quedas; honestamente, o branco era o menor dos males. Depois de alguns dias, esquiar torna-se mais natural, e uma das atividades mais divertidas que fiz. Basta aguentar o começo, as quedas, as dores, a neve, as crianças e o branco, esse branco profundo, resultado do bombardeio de tanto caos gerado por difração e refração que, entendido por nossos olhos, torna qualquer paisagem muito bela.

2 respostas

Abaixo de zero

Rookie

Sempre fico feliz quando uma notícia da física atinge o grande público, quando a mídia decide que algum descoberta forma uma frase de efeito digna de manchete, e nessa semana não foi diferente. Um grupo de físicos do Instituto Max Planck conseguiu criar um gás a temperatura negativa, abaixo do zero absoluto, e isso provocou manchetes muitas vezes enganosas e, apesar de algumas matérias terem saído interessantes, a maior parte era apenas um agregado de traduções de versões americanas feitas por quem não entende do assunto.

Temperaturas negativas não são novidade na física, elas têm até página na Wikipédia, e pretendo hoje, nesse post, tentar explicar o que queremos dizer com isso, e tentar esclarecer confusões lançadas pelas matérias sensacionalistas de física de folhetim. Para isso, precisamos entender o que é temperatura.

No princípio hesitei se poderia explicar esse tópico sem antes falar de um conceito fundamental da termodinâmica, e de toda a física, a entropia. Temia descobrir, enquanto escrevia, que eu mesmo não entendia o assunto, pois é uma das noções mais escorregadias da ciência. De forma extremamente simplificada, entropia é a medida da desorganização de um sistema. Preciso de um exemplo tão simplificado quanto minha explicação, vou usar um sistema a dois níveis de energia. Dificilmente encontramos algo na vida real que seja isso, mas pouco importa, quero apenas explicar o conceito. Imagine um sistema com $N$ partículas, sendo cada partícula capaz de estar em um estado de energia zero ou em um estado de energia $\varepsilon$.

dois_estados_2Se todas as bolinhas estiverem confinadas no estado zero, esse sistema tem entropia zero. Se todas estiverem confinadas no estado $\varepsilon$, o sistema também terá entropia zero. Mas se elas puderem se mexer, variar de um estado a outro, essa entropia será um valor maior, e positivo, indicando que o sistema não mais possui aquela ordem perfeita de antes e agora é uma mistura estranha de estados. A entropia indica quão bem feita é essa mistura, sendo máxima quando todas as configurações do sistema, todas as combinações de bolinhas em cima e embaixo, são possíveis e igualmente prováveis, ou seja, desordem completa, não posso afirmar nada sobre o estado atual do sistema, ele pode ser qualquer coisa.

A temperatura é a medida de quanto a entropia de um sistema varia quando damos energia a ele: quanto menor a temperatura, mais desorganizado um sistema fica com energia. Naturalmente, quanto maior for a temperatura, menos desordem um sistema ganha com a energia.

O fato da temperatura ser sempre positiva em nosso cotidiano é um reflexo da propriedade natural do aumento de entropia com o aumento de energia, como arrumar sua casa perfeitamente e lançar dentro dela uma ratazana raivosa, o equivalente da energia; dificilmente a casa ficará ainda mais organizada. Assim, apesar de sistemas com alta temperatura ganharem pouca entropia com energia, eles não perdem entropia.

Se deixamos nosso sistema de bolinhas a dois níveis interagir com o meio externo, ele poderá trocar energia com o meio e as bolinhas ganham ainda mais liberdade de subir e descer a ladeira. Se o sistema e o meio externo são muito diferentes quando entram em contato, eles vão trocar energia até que o quanto um sistema é desordenado pelo ganho de energia seja igual ao quanto o outro também é, ou seja, até que as temperaturas sejam iguais.

Isso é reflexo do princípio de máxima entropia, uma noção física que vai além das bolinhas e partículas, ligada profundamente a teoria da informação e probabilidades. Mais uma vez de forma bem simplificada, ele diz que, se você não tem uma boa razão para proibir um estado, o sistema atingirá esse estado e, se não tem uma boa razão para diferenciar dois estados, o sistema atingirá os dois com a mesma probabilidade. Em nosso problema das bolinhas, o sistema trocará energia com o meio externo até que o quanto ele causaria de desordem cedendo energia seja igual ao quanto ele ganharia de desordem ganhando energia, porque dessa maneira a entropia do processo todo (sistema + meio externo) será a máxima possível. Dessa forma, quando as temperaturas são iguais, isso significa que tanto o conjunto sistema + meio externo pode ocupar o maior número de estados possíveis de energia.

Como um gás lançado em uma sala vazia tende a se dispersar, não a se concentrar, porque eu não tenho uma boa razão para impedi-lo de ir para qualquer lugar da sala. Ele tende a ocupar todo o espaço e a chance de encontrar uma partícula em qualquer lugar é a mesma: isso é o princípio da máxima entropia. Se você conectar essa sala a uma outra vazia, pouco a pouco o gás vai ocupando também a outra sala até que todos os estados possíveis sejam ocupados com a mesma probabilidade.

Pelo princípio da máxima entropia, o gás tende a invadir a segunda sala e ocupar todo o espaço. A probabilidade de que ele fique todo na primeira sala é infinitamente pequena.

Se deixamos o sistema acoplado ao meio externo em uma temperatura fixa, ele trocará energia com o meio externo, e a temperatura será o quanto de desordem ele vai ganhar quando ganha energia. Se essa temperatura é baixa, o sistema ganha muita entropia com um pouco de energia. Isso acontece em situações como a de haver todas as bolinhas paradas na posição 0. Dar um pouco de energia significa permitir alguns saltos para o andar de cima, isso bagunçaria o sistema dando bastante entropia a ele. Se o sistema está em alta temperatura, como no caso de um gás quente, dar ainda mais energia não bagunçaria tanto o sistema.

Podemos escrever isso com alguma matemática. A chance de uma daquelas bolinhas estar em um estado de energia $E$ é dada por $\frac{e^{-E/T}}{Z}$, onde $e$ é um número especial entre 2 e 3 e $Z$ é alguém que multiplicamos para que a probabilidade não seja maior que 1 (para quem começou a ver física estatística, essa é a distribuição de Boltzmann!). É fácil ver que a chance de estar no estado de energia 0 é $1/Z$, enquanto a chance de estar no estado $\varepsilon$ é $\frac{e^{-\varepsilon /T}}{Z}$. Isso representa um fato físico famoso: é mais fácil estar em um estado de baixa energia que em um de alta energia. Quanto menor a temperatura, mais difícil é encontrar alguém em um estado de energia alta. Quanto maior a temperatura, mais ambos os estados ficam com probabilidades parecidas. A maior parte dos sistemas físicos funciona dessa exata maneira.

No entanto, se você conseguir ser malandro, como os físicos do Instituto Max Planck, e criar um sistema físico bem patológico tal que estados de energia mais alta são mais prováveis, como você explica usando esse formalismo? Ora, basta dizer que são estados a temperatura negativa. Dessa forma, $\frac{e^{-\varepsilon /T}}{Z}>1/Z$ e você consegue continuar a trabalhar com esses sistemas usando sua matemática favorita.

É porque associamos temperatura a essa taxa de ganho de desordem que podemos interpretar desse jeito estranho. Temperatura não é mais o movimento das partículas, isso ficou com os gases ideais no colegial, ela agora é a medida do ganho da desordem em função da energia. E se um sistema começa a privilegiar estados de energia alta, interpretamos isso como uma temperatura negativa.

Ouvi muito a respeito, inclusive da Wikipédia, sobre a temperatura negativa ser o limite de uma temperatura tão positiva que ela “dá a volta” e vira negativa. Como dizer que os reais são um corpo cíclico me causa urticária, tento explicar o que isso significa. Uma temperatura muito baixa favorece muito estados de baixa energia. Uma temperatura alta não favorece ninguém, e quanto mais alta, menos favorecimento possui. Se atingíssemos a temperatura $+\infty$, teríamos passado de uma situação de favorecimento das energia baixas a não favorecer ninguém. Se fôssemos “além” do $+\infty$, teríamos uma situação que privilegia as altas energias, e é isso que aquela explicação estranha quer dizer. Não gosto dela, e paro a explicação da explicação por aqui.

Resumindo: os cientistas do Instituto Max Planck conseguiram criar um sistema patológico o suficiente para deixar os estados de alta energia mais prováveis que os de baixa energia. Na matemática da física estatística, isso é interpretado como uma temperatura negativa, pois temperatura é o que mede essa preferência por estados de baixa energia. Isso não é nada chocante ou escandaloso, é interessante que eles tenham conseguido isso para um sistema quântico bem complicado, o artigo original está aqui, mas, infelizmente, é mais uma manchete para vender jornal que um grande avanço para a termodinâmica.

Assumo que o post ficou confuso, mas é um tema complicado. Um dia sento e escrevo algo mais claro sobre entropia, no mesmo dia em que tomar coragem para ler a montanha de textos a respeito da interpretação física dela. Precisaria selecionar, ler, escrever, revisar tanta coisa que, em matéria de desordem, deixo exatamente como está.

4 respostas

Crime e castigo

Rookie

Há algum tempo, inspirado em um comentário desse blog, queria escrever algo sobre o fenômeno estatístico conhecido como regressão à média. Desde pequeno fui fascinado pela análise teórica do sermão que recebia de meus pais a cada travessura que aprontava. Quebrei janelas, copos, sujei-me, sujei a casa, nada voluntário, coisa de criança; mas recebia, a cada evento, a devida repreensão de pai ou mãe (ou dos dois, não eram excludentes). Também levava broncas por notas mais baixas, não tantos elogios pelas altas, que eram, afinal, minha obrigação. Achava que as coisas eram daquele jeito, que não poderia ser de outro jeito, até, entrando na faculdade, conversar com um amigo que cursava administração de empresas. Segundo ele, muito mais eficaz que esse método era o inverso, o tal do positive reinforcement, elogiar o que é bom e trabalhar no que está ruim, mostrar ao time vídeos com seus acertos ao invés de erros, meu amigo citava experiências sociológicas e psicológicas bem interessantes para provar seu ponto, mas eu custava a acreditar.

Dizer que a recompensa é o melhor caminho choca nossa experiência. Estamos habituados a ver resultados melhorarem após a repreensão, e muitos dizem que, após o elogio, o elogiado tende a piorar e a decepcionar, como se elogiar estragasse, como se ficar feliz e orgulhoso o tornasse relaxado. O post de hoje serve para desarmar esse argumento, e nossa ideia de que alguém “aprendeu a lição” após uma bronca bem tomada. Vou argumentar que esse fenômeno de fato existe, a piora em relação ao elogio e a melhora em relação à bronca, mas que ele reflete muito mais uma verdade estatística que uma mudança de comportamento.

Vamos imaginar uma criança, Denis, o pimentinha, que, ao decorrer do ano letivo, fará 20 provas. Ele não é o melhor da sala, nem o pior, e estuda um pouco para cada prova, mas não muito. Denis estuda suas matérias para tirar um 7,0, que é uma nota boa em sua opinião. No entanto, algumas vezes a prova é mais fácil, ou mais difícil, então sua nota varia; sua média é constante, mas as flutuações são aproximadamente de dois pontos em sua nota. Ou seja, vamos tratar a nota de Denis como uma variável aleatória de média 7,0 e distribuição normal com variância 1. Dessa forma, a chance de ele tirar acima de 9,0 é de 2,2%, e a chance de tirar abaixo de 5,0 também é de 2,2%, sendo 68,2% a probabilidade de ele tirar entre 6,0 e 8,0.

Esses números podem parecer estranhos, mas esse modelo é um dos mais adequados para representar tarefas humanas, a chamada distribuição gaussiana, ou distribuição normal. Ela diz que teremos um valor esperado (no caso de Denis, 7,0), mas que teremos dias bons e ruins. A maior parte dos dias (68,2%) não será muito longe do valor esperado (entre 6,0 e 8,0), mas alguns, excepcionais (2,2%), podem ser muito bons (acima de 9,0, caiu exatamente o que ele havia estudado!) ou muito ruins (abaixo de 5,0, não caiu quase nada do que ele sabia).

Sua mãe se preocupa com sua educação, e o disciplina como sua mãe a disciplinou. Ela dá um presente a Denis cada vez que ele tira uma nota acima de 9,0, e o castiga cada vez que ele tira uma nota abaixo de 5,0. Vejamos como seriam as notas de Denis em um ano:

O que a mãe de Denis entenderá desse gráfico? Note que toda vez que ela castiga Denis, suas notas tendem a subir, enquanto toda vez que ela o presenteia, ele tende a tirar notas piores! É importante notar que isso nada diz sobre o aprendizado de Denis, eu apenas tirei notas aleatoriamente, dizendo que Denis é um aluno nota 7,0 que tem dias bons e ruins.

Essa ilusão da eficácia do castigo ocorre porque é muito raro ter dois dias ruins seguidos, e a ilusão da ineficácia do elogio é pela também raridade de dois dias excepcionalmente bons. O valor seguinte ao de um dia excepcional tende a ser menos espetacular, ou, como dizemos, tende a regredir à média dos valores.

Note, eu não estou dizendo que o castigo tem eficácia zero no comportamento, ou que o presente também não tem efeito, estou apenas dizendo que o raciocínio de punir e melhorar e não elogiar para não estragar pode ser aplicado até a variáveis aleatórias. Certamente a maneira como uma pessoa é tratada influencia em sua performance, mas uma teoria de castigo e recompensa que pode ser explicada pelo mero acaso, pela estatística, não pode ser tida como uma grande verdade sobre o comportamento humano.

Em outras palavras, imagine-se alguém que considera tirar menos que 5 em um sorteio para o próximo número do bingo algo ruim, e que considera tirar mais que 95 um resultado bom. Você pode, por algum motivo, culpar aquela esfera engradeada que vomita os números pelo resultado, e eu garanto: se você der uma bronca nela após cada resultado menor que 5, ela vai muito provavelmente melhorar bastante na próxima vez. Se você elogiar a cada resultado acima de 95, ela provavelmente irá te decepcionar na próxima bola sorteada.

Não quero, nem pretendo, dizer que broncas são ineficazes, ou que a única resposta possível para educar ou ensinar são elogios, paz e amor. Lanço esse post na polêmica opinião que pede uma revisão de nossos conceitos da eficácia do castigo como aprendizagem. Para que você se pergunte quanto do que você aprendeu veio dos benefícios de um sermão, ou, ainda, quanto de cada melhora que viu após uma bronca foi resultado dessa bronca ou se foi, por puro acaso, um dia melhor que ontem.

2 respostas