Quando era criança, fui atingido pela mania dos tazos da Elma Chips como todos os meus colegas. Abria o salgadinho antes mesmo de chegar à aula, longe ainda do recreio, e recolhia o precioso prêmio do pacote: um disco plástico que servia de moeda de aposta e demonstração de habilidade no intervalo. Eu não era muito bom nisso, e não tinha tantos amigos, então minha principal fonte de Tazos eram o fandangos.

Via colegas com tubos repletos de tazos, coleções completas, era invadido por essa inveja e, talvez mais, por uma pergunta séria: como aquilo era possível? Eu colecionava havia meses e não chegara perto da metade da coleção, possuía muitos repetidos e aquele do Papa-Léguas era mais difícil de encontrar que filhote de pomba. Não imaginava como aquilo era possível, culpava os pais do garoto sortudo, deviam ter comprado caminhões de baconzitos, e, no fundo, queria saber: de quantos fandangos eu precisaria para completar minha coleção?

Essa pergunta está mal-feita, vamos melhorá-la. Mais interessante seria perguntar: qual o número médio, o valor esperado, de salgadinhos que preciso comprar para completar minha coleção? Em outras palavras, a partir de qual número de fandangos é mais provável que eu já tenha a coleção completa que o contrário? E, como pergunta bônus, quão improvável se torna, a partir desse número, não obter os preciosos tazos?

Havia tazos mais raros, é verdade, mas a pergunta já está bem difícil, então tomo como hipótese que a chance de tirar qualquer um dos tazos é a mesma. E para continuar, precisamos primeiro saber quantos são eles, e eis a coleção toda:

Se você está interessado na resposta, mas não conhece tanto de probabilidade, o que segue não será tão interessante (vou fazer as contas, é o que faço da vida, não consigo evitar). Mas você pode pular para o final do post e ver as conclusões sem culpa, se confiar em mim. Se, no entanto, você entende de probabilidade, jamais confie em mim. Suponha que eu já tenha $ k$ tazos diferentes, sendo $ n$ possíveis, a chance de eu tirar um repetido é $ \frac{k}{n}$. Assim, a probabilidade de eu precisar de exatamente $ s$ salgadinhos para tirar um diferente é $ \left(\frac{k}{n}\right)^{s-1} \left(1-\frac{k}{n}\right)$, que é uma parte a chance de eu tirar $ s-1$ repetidos e outra parte, no $ s$-ésimo salgadinho, tirar um diferente. Essa é $ P(s)$, a chance de eu precisar de $ s$ fandangos para tirar meu tazo diferente. Para calcular o valor esperado de salgadinhos até o próximo tazo diferente, ou seja, de $ s$, basta tomar:

\[ \sum_{s\geq 0}P(s).s=\sum_{s\geq 0}\left(\frac{k}{n}\right)^{s-1}\left(1-\frac{k}{n}\right).s=\frac{1}{1-\frac{k}{n}}\]

Essa última passagem fiz na malandragem, vale a pena explicar. Vou chamar $ \frac{k}{n}$ de $ x$ porque digitar essas coisas no WordPress cansa. Vou aplicar a distributiva, manobrar os índices e converter tudo em uma progressão geométrica de soma bem fácil:

\[\sum_{s\geq 0}x^{s-1}\left(1-x)\right).s=\sum_{s\geq 0}x^{s-1}s-\sum_{s\geq 1}x^s.s=\sum_{s\geq 0}x^s(s+1)-\sum_{s\geq 0}x^s.s=\sum_{s\geq 0}x^s=\frac{1}{1-x}\]

Então o número esperado de salgadinhos que devo comprar é a soma dos salgadinhos esperados para cada tazo que vou tirando, ou seja:

\[ \sum_{k=0}^{n-1}\frac{1}{1-\frac{k}{n}}=\frac{n}{n}+\frac{n}{n-1}+\ldots+\frac{n}{2}+\frac{n}{1}\]

Sem magia até agora, eu apenas expandi a série. Eu poderia calcular exatamente esse valor para $ n=80$, mas gosto de resultados mais gerais, e noto que essa soma é $ n$ vezes a série harmônica. Ela diverge, e não é surpreendente que eu precise de infinitos fandangos para tirar infinitos tazos, mas felizmente conhecemos razoavelmente bem o comportamento dessa série. O número esperado de salgadinhos necessários para completar uma coleção de $ n$ tazos é, portanto, $ nH_n$, onde $ H_n$ é o n-ésimo número harmônico. Para $ n$ grande, podemos usar a aproximação $ H_n\approx \log n+\gamma$, onde $ \gamma$ é a constante de Euler-Mascheroni (aproximadamente 0,5772).

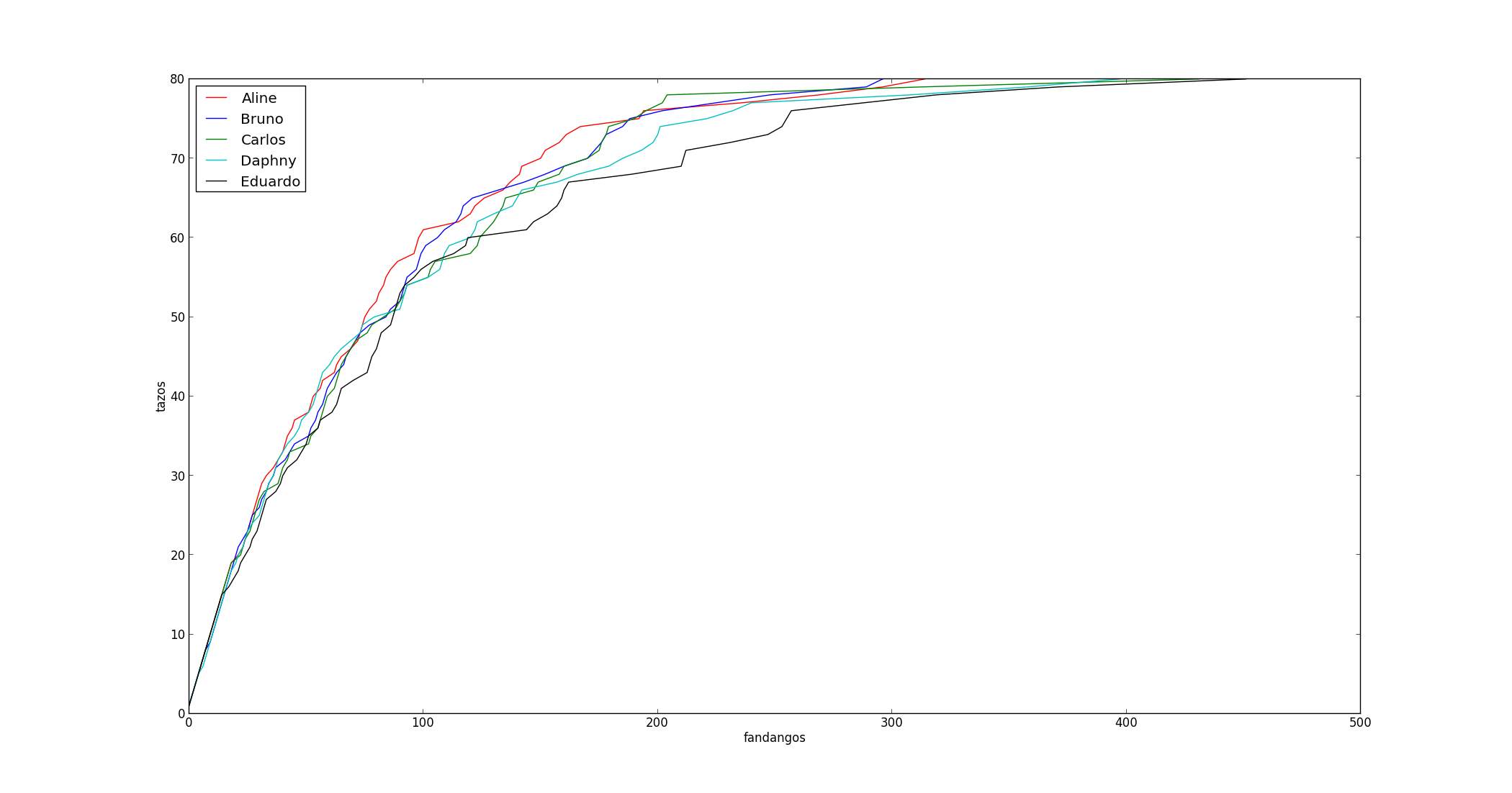
Chegamos ao valor $ 80*(\log(80)+\gamma)=396,74$, certamente aproximado. Esse é o número médio de vezes que crianças completam suas coleções. Temos a média, a próxima pergunta é: quão provável é estar longe da média? Ao invés de tentar calcular com manobras intrincadas as flutuações desse número em torno da média, tomarei, a princípio, o exemplo de cinco crianças: Aline, Bruno, Carlos, Daphny e Eduardo. Eles começam suas coleções juntos e têm poucos amigos, logo, contam apenas com os salgadinhos para obter os preciosos discos. Eis uma simulação que fiz do resultado da coleção dessas cinco crianças:

Notamos algumas coisas interessantes. Primeiro, teremos que gastar aproximadamente metade dos salgadinhos totais necessários apenas para conseguir os dez últimos tazos; a matemática é cruel com coleções quase completas. Segundo, o valor necessário para completar é muito diferente nos cinco casos, isso exige um estudo mais sério.

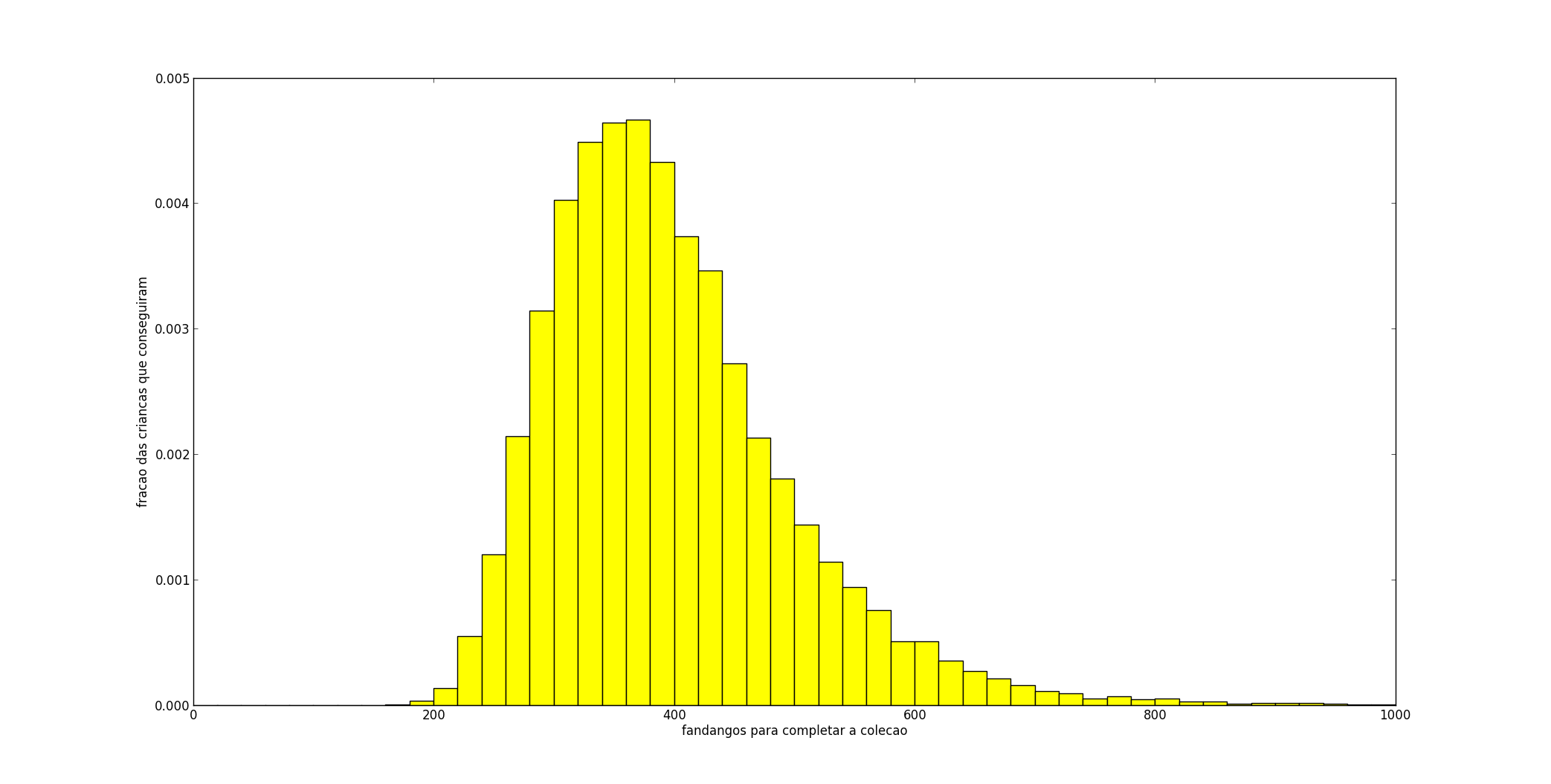
Para tal, calibramos o computador para simular a coleção de tazos, ou o álbum de figurinhas (o problema é o mesmo) de 20.000 crianças. Fiz um histograma com a quantidade de salgadinhos necessária para completar toda a coleção e a porcentagem das crianças simuladas que precisaram daquela quantidade de salgadinhos para obterem o último tazo.

Notamos a larga variância dessa distribuição: haverá um grande número de crianças sortudas e um grande número de azaradas! Confirmamos o valor esperado, 396 parece de fato uma boa média dessa distribuição, e confirmamos o quão sórdido é o raciocínio da Elma Chips: algumas crianças precisariam de 900 salgadinhos para terem a coleção completa!

Contudo, esse modelo não representa bem a realidade, talvez apenas a minha, mas a maior parte das crianças tinha como maior objetivo as trocas de tazos, as disputas, completar a coleção contando com o salgadinho dos outros. Eu mesmo consegui dois amigos para fazer uma sociedade, ainda que cada um quisesse, para si, uma coleção completa. E esse será meu modelo de trocas: os amigos são amigos perfeitos, todo tazo repetido é compartilhado e o objetivo maior é, para $ y$ amigos, formar $ y$ coleções completas.

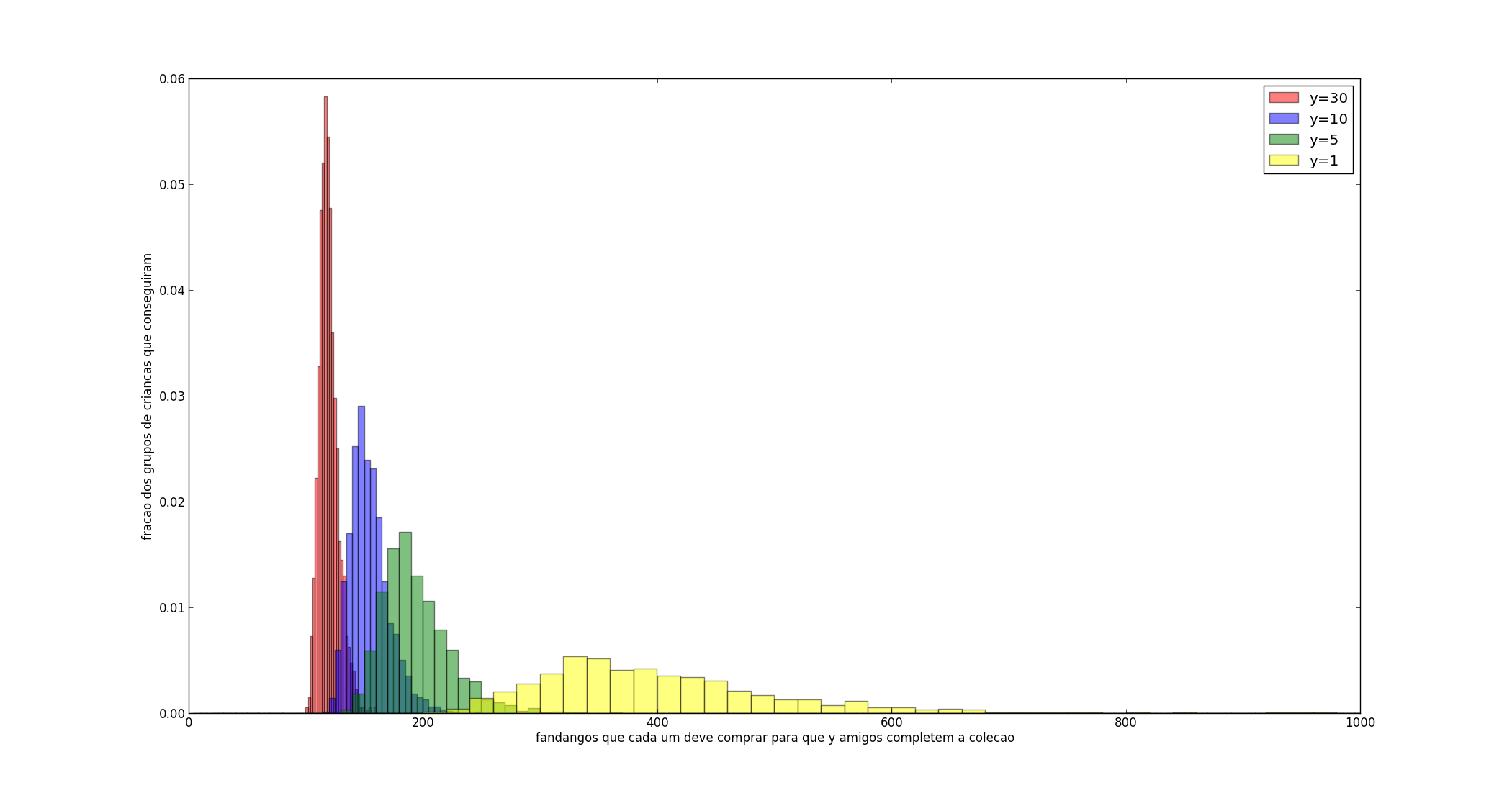
De forma não surpreendente, o número de fandangos que cada criança deve comprar reduz drasticamente com as trocas. Se ele antes precisava gastar quase um ano de lanches de salgadinho para encontrar os dez últimos, esses famigerados dez podem ter sido encontrados por algum colega que já até o tirou uma vez. Simulei o resultado com grupos de 1, 5, 10 e 30 crianças, sendo os resultados no histograma abaixo:

Esses valores são quantos fandangos cada um precisará comprar, ou seja, no grupo de dez, se dez amigos precisaram de 2000 fandangos para fechar a conta, contabilizo 200 para cada criança. Os valores médios de salgadinhos individuais obtidos para 1, 5, 10 e 30 são, respectivamente e aproximadamente, 398, 194, 154 e 120. Fiquei curioso para estudar a convergência dessa série, se vai para algum lugar (certamente converge, sendo decrescente e limitada em 80) e se esse lugar é 80, uma utopia em que todas as crianças do país montam suas coleções juntas; mas esse post já está longo e tanto salgadinho não deve fazer bem a esses meninos.

Por fim, noto que a amizade é o melhor investimento, você pode, em poucos meses de lanche, completar sua coleção de tazos ou figurinhas se encontrar, em uma sala de aula, trinta amigos perfeitos. A probabilidade desse fato, no entanto, mesmo em um modelo bem otimista, é extremamente baixa.