No post de hoje, vamos resolver um problema grave, clássico e profundo: como escolher o melhor namorado ou namorada para casar, ou como escolher o melhor garoto ou garota na balada para levar para casa aquela noite. Não são problemas simples, mas, como a maior parte dos dilemas pessoais, usando frieza, crueldade e fechando os olhos para os reais problemas sociais envolvidos, podemos tirar conclusões bem interessantes. No post de hoje, vamos deduzir a estratégia para maximizar suas chances de, em uma noite, levar o melhor parceiro possível para seu quarto mostrar sua coleção de discos do Elvis.

Deixo apenas registrado que se você está buscando referências sérias nesse blog sobre como se dar bem em uma balada, deve estar realmente desesperado. Continuemos.

O problema se apresenta da seguinte forma: você pegará na noite de hoje um número $N$ de pessoas. Dentre essas pessoas, você estabelece um ranking de qualidade, seu objetivo é levar a melhor delas para casa porque, convenhamos, você já passou da idade de ficar só dando beijinho em balada. Você encontra uma pessoa, corteja, afeiçoa-se e tem duas opções: ou escolhe essa para levar para casa, ou rejeita. O problema é claro: você corre o risco de estar rejeitando a melhor dentre as $N$. Supondo que você e a pessoa têm um pingo de dignidade, não poderá voltar atrás nessa decisão! Nessa lógica, qual a melhor estratégia para maximizar suas chances de escolher de fato a melhor dentre as $N$ possíveis?

Se achou as contas a seguir chatas e complicadas, tudo bem, eu entendo; você pode pular para o final do post para descobrir a melhor estratégia.

A natureza do seu dilema é a informação incompleta. Cortejando a pessoa número $n$, você tem apenas o ranking dela em relação às que já viu, não tem a menor ideia de como ela se compara às que virão. A primeira pessoa sempre será a melhor até então (e a pior), não parece uma boa estratégia aceitar a primeira que aparece, porque a noite é longa e promete. Por outro lado, se você encontrar a melhor até então na penúltima pessoa, as chances são baixas de encontrar a melhor de todas na última, desprezar a melhor na penúltima parece também uma estratégia ruim. Entre uma recusa quase certeira da primeira e uma aceitação quase certa da penúltima, deve haver algum ponto intermediário em que a estratégia fica a melhor possível.

Vamos calcular esse ponto e determinar qual a melhor estratégia para o problema. Para isso, vamos primeiro modelizar o problema de forma precisa:

• Você estima que cortejará $N$ pessoas até o final da noite.
• Uma vez rejeitando a pessoa, não pode voltar atrás.
• Seu ganho é 1 se você escolher a melhor dentre as $N$ pessoas e 0 se escolher qualquer outra.
• Se chegar à última, leva a última. Em outras palavras, se a balada começou a miar e são seis da manhã, você leva para casa a pessoa que sobrou, sinto muito. Nisso, convenhamos que o modelo é bem preciso.

Confesso que o modelo tem um problema, a noção de tudo ou nada, de que seu ganho é zero ainda que você leve a segunda melhor, enquanto, convenhamos, não é algo tão ruim. Vamos imaginar que você é extremamente exigente e sentirá que a noite não valeu a pena porque, levando a segunda melhor, pensará apenas na primeira durante a noite toda.

Para resolver o problema, vamos definir duas variáveis. $X_n(1)$ é o seu ganho esperado se na $n$-ésima pessoa entrevistada você encontrar a melhor até então; $X_n(0)$ é seu ganho esperado caso a $n$-ésima entrevistada não seja a melhor vista até então. Em nosso modelo, claro, $X_n(0)=0$, você não espera ganhar nada levando alguém para casa que nem é o melhor dos primeiros $n$ que você já viu, vale mais tentar outras pessoas e correr o risco de encontrar o melhor nos seguintes. Se você encontrar na $n$-ésima a melhor até então, o seu ganho é a chance de a melhor pessoa estar entre as $n$ primeiras. Como a ordem em que você pega as pessoas é aleatória, essa chance é de $n/N$. Assim, $X_n(0) = 0$ e $X_n(1)=n/N$.

Em seguida, definimos o ganho esperado se descartamos a pessoa $n-1$ e passamos para a $n$, chamamos essa variável de $Y_n$. O seu ganho esperado descartando a pessoa $n-1$ depende do que você vai fazer encontrando a pessoa $n$. Se você decidir ficar com a pessoa $n$, seu ganho esperado saltando $n-1$ é o ganho esperado de $n$, ou seja, $X_{n}$. Se você decide saltar também a $n$, então seu ganho esperado será $Y_{n+1}$. Você vai tomar essa decisão baseando-se nesses valores, você deve se perguntar “Quem é maior: $X_{n}$ ou o valor médio de $Y_{n+1}$?”. Comparando esses dois valores, você sabe qual será seu comportamento no próxima pessoa. A fórmula para $Y_n$ será, portanto, definida de forma recursiva:

\[ Y_n = \max \{X_{n},\langle Y_{n+1} \rangle \} \]

Onde $\langle x \rangle$ é a média de $x$, escrita desse jeito com o único objetivo de fazer os estatísticos lendo esse texto terem um pequeno derrame de nervoso.

Esse cálculo recursivo encorpora bem o dilema descrito acima. Perto das últimas escolhas, $X_n$ fica grande se você encontra a melhor pessoa até então e $Y_n$ fica pequeno. No início, contudo, $X_n$ é pequeno e vale mais apostar no futuro do que estacionar no começo. Para que a fórmula recursiva faça sentido, ela precisa ter um ponto de partida. Nisso usamos a última hipótese, o ganho esperado pulando a última casa é o mesmo que o da última casa, ou seja, pular a última não adianta, você leva a última opção se chegar nela: $X_N=Y_N$. Usando a fórmula acima, e com algum malabarismo que não cabe aqui, você consegue deduzir a expressão de $Y_n$:

\[ Y_n = \frac{n}{N}\sum_{k=n}^{N-1} \frac{1}{k} \]

Assim, começa a valer a pena escolher uma pessoa a partir do momento em que $X_n > Y_n$, ou seja, quando estamos na $k$-ésima pessoa e $1>\sum_{k=n}^{N-1} \frac{1}{k}$. A partir desse valor, seu ganho esperado ficando com a melhor pessoa encontrada até agora é maior que o ganho esperado no futuro pulando essa pessoa; logo, é estatisticamente mais interessante levar essa para casa.

Claro que encontrar esse valor de $k$ não é simples, tem que somar fração e isso é chato, tem umas partes que envolvem MMC e isso me dá fadiga. Melhor que somar essas frações seria usar uma boa aproximação para essa soma, que eu conheço bem, é a série harmônica $\sum_k \frac{1}{k}$. Como você deve se lembrar de sua infância, essa soma de 0 a $n$ pode ser aproximada, para grandes valores de $n$, por $\ln n $. Assim, a soma de $n$ até $N-1$ deve ser $\ln (N-1)-\ln(n) = \ln\left(\frac{N-1}{n}\right)$. Como usamos a hipótese de valores grandes de $N$, podemos escrever isso como $\ln\left(\frac{N}{n}\right)$. Assim, devemos parar de pular candidatos quando encontramos o melhor a partir do $n$-ésimo, sendo $n$ o número tal que $\ln\left(\frac{N}{n}\right)<1$, ou seja, $n = \frac{N}{e}$, onde $e$ é o número de Euler $e=2,71828\ldots $.

Percebemos que essa conta nos diz para pularmos os primeiros $\frac{N}{e}$ pretendentes e, após esses, ficar com o primeiro que for melhor que todos os anteriores. Note que $\frac{1}{e}\approx 0.37$. Em outras palavras, a estratégia optimal para encontrar o melhor pretendente da balada para levar para casa é a seguinte: estabeleça um número de pessoas para pegar na balada. Rejeite necessariamente os primeiros 37% delas. Cole na primeira pessoa que aparecer que for melhor que todas as anteriores e leve esta para casa.

O mesmo vale para namorados ou namoradas durante sua juventude. Se quer maximizar suas chances de casar com a melhor opção, estabeleça uma estimativa do número de pessoas com que vai namorar durante sua vida, termine com os primeiros 37% e case com a primeira que aparecer que for melhor que todas as anteriores.

Vamos ver quão bem isso funciona. Para isso, vamos contar a história de Pedro.

Pedro é um garoto que costuma ir a três baladas diferentes. Ele está atrás de garotas, e quer levar a melhor delas para casa. As baladas são diferentes, e a qualidade dos frequentadores tem uma distribuição variada para cada balada. Vejamos quais são elas, usando descrições do site cidadedesaopaulo.com:

1.  A The History, localizada na Vila Olímpia, tem piso que muda de cor e agrada tanto àqueles que já curtiram os hits dos tempos da brilhantina quanto às novas gerações. Possui um público pouco variado e previsível, a qualidade dos frequentadores será dada por uma distribuição gaussiana.
2. Localizado no Baixo Augusta, o Beco 203 é reduto dos moderninhos e alternativos que curtem um rock mais soft e festas em que o som é tocado através de fones de ouvido. Atraindo um público mais variado, a distribuição da qualidade de seus frequentadores será dada pela distribuição uniforme.
3. A Lab, localizada na Rua Augusta, possui em sua programação dias dedicados à música eletrônica. Com um público ligeiramente variado, mas não muito, a qualidade de seus frequentadores está mais concentrada nas piores notas que nas melhores e será modelada pela distribuição exponencial.

Pedro é uma máquina e se dispõe inicialmente a pegar 100 garotas. Ele vai vezes o suficiente às baladas para poder testar diferentes estratégias, e está disposto a tentar todas as possibilidades. A experiência é a seguinte: um dia ele leva a primeira que encontrar para casa. No dia seguinte, ele rejeita a primeira e leva a primeira melhor que as anteriores para casa. Em seguida, rejeita as duas primeiras e leva a primeira melhor que as anteriores que encontrar para casa. Fazendo isso até a centésima vezes o suficiente, ele consegue estimar a taxa de sucesso de cada estratégia. Uma noite é bem sucedida se a que ele levou para casa era a melhor dentre as 100 possíveis. São bastantes opções, vejamos qual a taxa de sucesso de cada uma das estratégias.

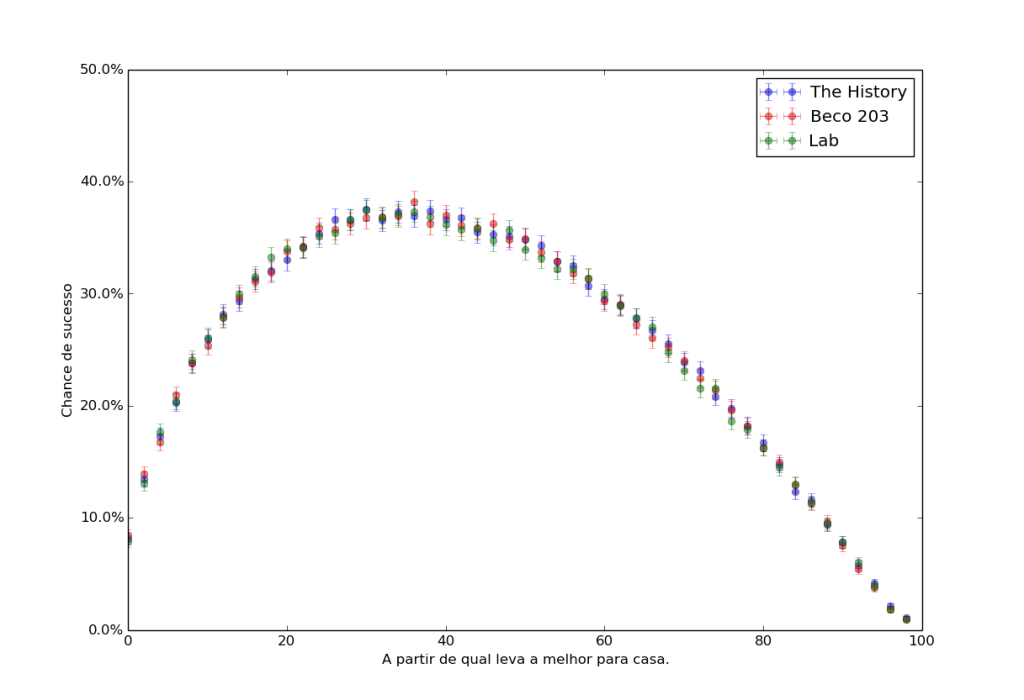É facil acreditar que o valor ideal para a estratégia é 37, ou seja, rejeitar os primeiros 37% e aceitar a primeira opção melhor que todas as anteriores. Note como esse valor independe de como a qualidade das pretendentes está distribuída, seja uniforme ou extremamente concentrada em torno da média, a eficácia de cada estratégia é a mesma.

Falando um pouco mais sério, esse pequeno problema estatístico revela uma matemática internalizada em diversas decisões em nosso cotidiano, a ideia de “assentar”, de escolher uma opção para ser a definitiva. Quando você é jovem, seus namoros são em média curtos, explosivos, cheios de emoções e problemas, a idade vai trazendo mais estabilidade e em um ponto da vida você encontra aquela que acha ser a pessoa certa. Você experimentou o suficiente para identificar uma pessoa melhor que as anteriores e entender que a melhor estratégia é juntar os chinelos com esta; porque, conhecendo as alternativas, você prefere não arriscar e entende que é pouco provável encontrar algo tão melhor nas futuras opções. Casamento é sobre amor, sobre almas gêmeas, some encontrar a pessoa prometida e amada; mas quando você começa a beirar os trinta anos a realidade bate na porta e a estatística, aliada a sua experiência, fala mais alto.

E se você me perguntar se sigo essa estratégia, não vou poder responder. O modelo tem várias hipóteses, várias delas são boas, a maior parte se aplica a minha situação, mas um grande valor de $N$, certamente, não é o caso.