Hoje é meu aniversário, celebro vinte e quatro anos de vida. E essa data, além de me fazer sentir especial, costuma me lembrar de um problema fascinante de combinatória, que levou a um igualmente interessante estudo econômico. Como não achei referência ao estudo, nem lembro onde o li, repeti-o eu mesmo, na medida do possível. O problema é conhecido como paradoxo do aniversário, que de paradoxal não tem nada.
A pergunta é: quantas pessoas eu preciso colocar em uma sala para que a chance de haver naquela sala pessoas com o aniversário repetido seja maior que a chance de não haver pessoas com o aniversário repetido? Formulado de outra maneira, eu tenho $N$ pessoas em uma sala e uma probabilidade $P(N)$ de que essas pessoas possuam aniversário repetidos, qual o primeiro valor de $N$ para o qual $P(N)>0,5$?
E a resposta é um número surpreendentemente baixo: 23. A partir desse valor de pessoas, é mais provável encontrar pessoas com aniversários repetidos que não encontrar, a probabilidade de que duas pessoas tenham nascido no mesmo dia do ano passa a 50,7% para esse valor de $N$. A razão do número ser pequeno é o grande crescimento da função fatorial, usada para calcular o número de combinações possíveis para a comparação de cada par de pessoas. Ou seja, apesar de haver muitos dias no ano, o número de comparações possíveis entre o aniversário de 23 pessoas é suficientemente grande para tornar essa probabilidade maior que 50%.
Interessados nesse resultado, podemos testar os aniversários de partidas de futebol. Sendo 11 para cada lado e o juiz, teremos 23 pessoas a cada partida, e podemos comparar um número grande de partidas para perceber que há mais partidas com aniversários repetidos que partidas sem aniversários repetidos.
No entanto, o resultado não será o que esperamos. De fato, há muitas partidas com aniversários repetidos, mas um número muito maior que o esperado! As partidas com aniversários repetidos ocorrem em número muito maior que as que não possuem aniversários em comum, quando a diferença não deveria estar muito longe de 51% contra 49%. Esse fato foi-me apresentado há algum tempo, foi-me até dito que um estudo foi feito, jamais achei o estudo, fi-lo eu mesmo com a ajuda da Wikipédia e sua excelente página da escalação de cada seleção de futebol.
Pus-me a anotar os meses de nascimento dos jogadores de futebol das seguintes seleções: Brasil, Paraguai, Chile e Argentina. Tomei a escalação mais atual possível, para não haver privilégio de uma época ou outra. A razão de pegar apenas países do hemisfério sul ficará clara com os resultados.
Enquanto o Paraguai não apresenta uma distribuição de nascimento de seus jogadores ao decorrer do ano que chame a atenção, Brasil, Chile e Argentina impressionaram-me e comprovaram, em termos nada rigorosos, a teoria que eu havia ouvido a respeito do estudo. Organizei um histograma em três camadas, as barras menores são os nascimentos no mês, as intermediárias representam nascimentos em um trimestre e as grandes são os nascimentos no semestre. O resultado do Paraguai, analisados 83 jogares, foi:
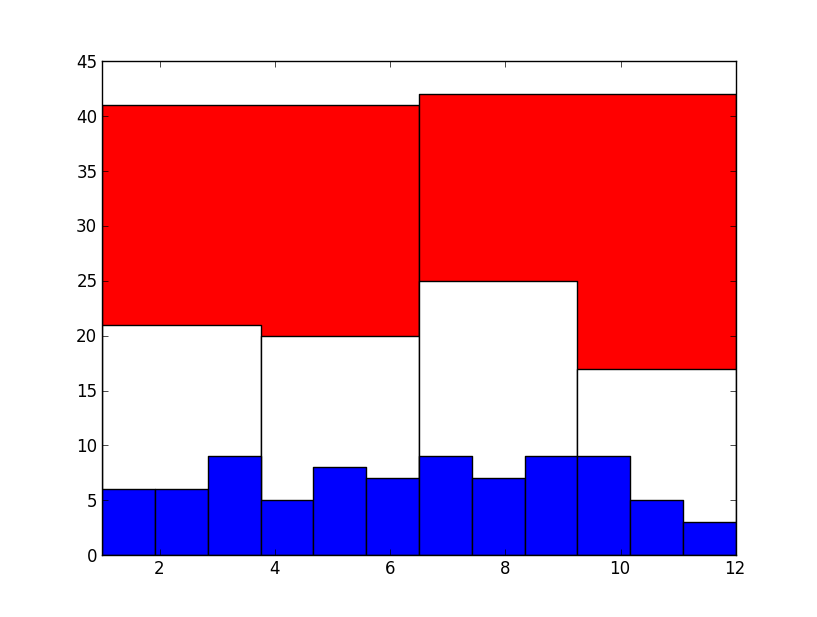
Nada impressionante até aqui, os aniversários parecem razoavelmente bem distribuídos em todos os níveis e não consigo perceber uma tendência evidente. No entanto, a distribuição do Brasil já começa a apresentar um fenômeno interessante:
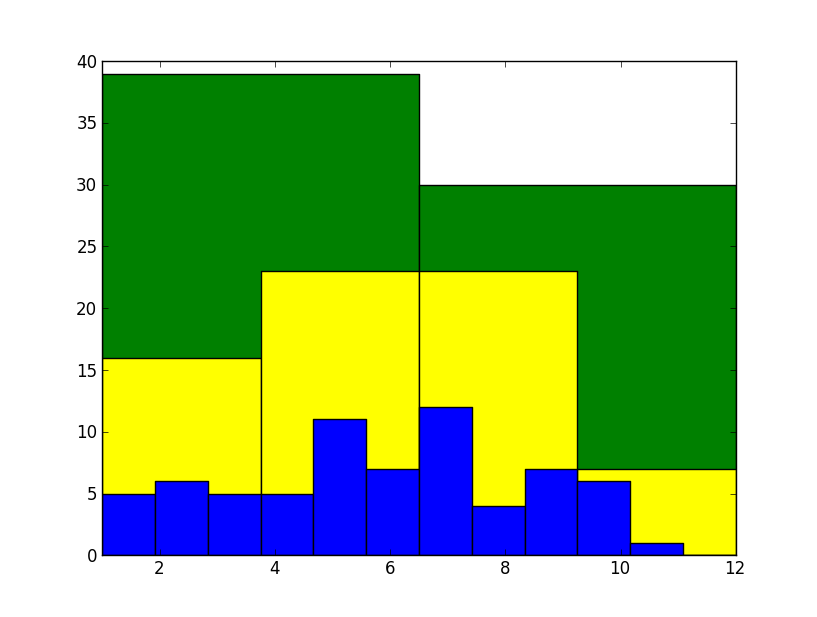
Temos na seleção brasileira, analisados os 69 últimos convocados de Mano Menezes, uma concentração clara de nascimentos no primeiro semestre, em especial uma forte ausência de nascidos no último trimestre do ano. Claro, isso pode ser uma improbabilidade realizada, não um indício de variável escondida. Se analisarmos com cuidado, podemos calcular a probabilidade de, jogando aniversários aleatoriamente no ano, ter essa diferença entre o primeiro e o segundo semestre; é improvável, mas nem de longe impossível.
No entanto, os resultados do Chile, analisados 77 jogadores, revelaram-se:
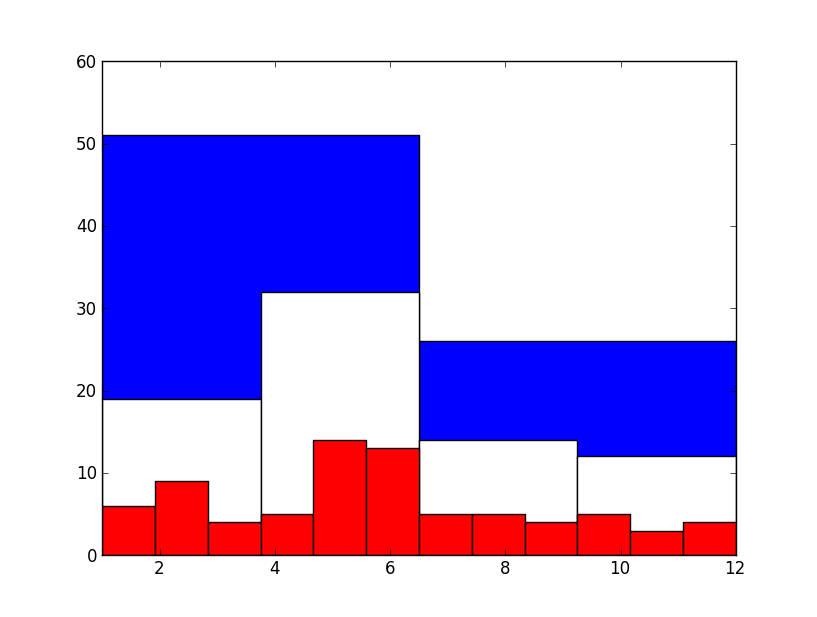
E essa diferença entre primeiro e segundo semestre já não pode mais ser explicada como uma anomalia estatística, há algo estranho nesse país que faz jogadores de futebol nascerem no começo do ano e não no final. Para confirmar a teoria, podemos avançar no estudo da seleção Argentina, analisando 92 jogadores:
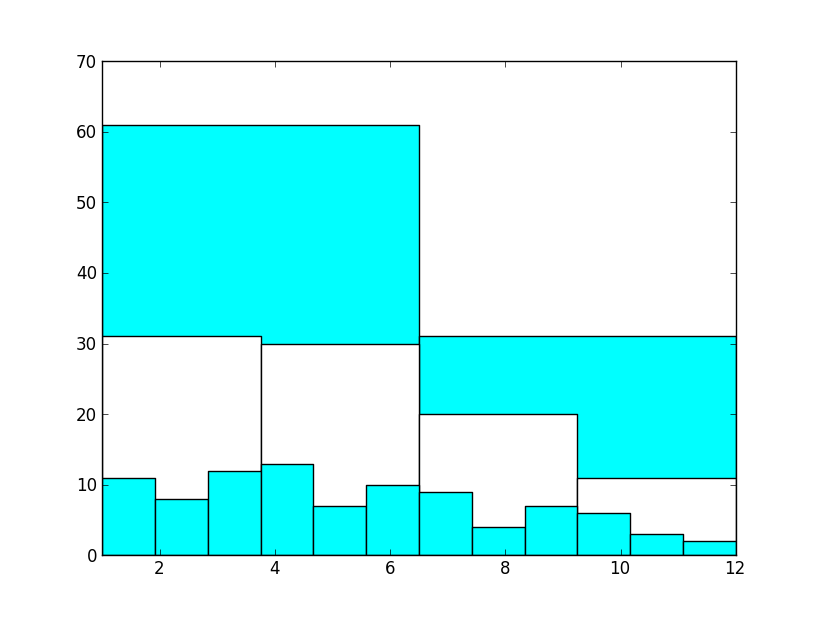
Esse gráfico não pode, de maneira alguma, ser justificado como coincidência. A albiceleste possui o dobro de jogadores nascidos no primeiro semestre em relação ao segundo semestre. Entrementes, notamos que em todas as seleções dezembro é sistematicamente o pior mês, ou o segundo pior, no caso do Chile.
Podemos nos divertir calculando a probabilidade de obter uma configuração como a da Argentina se os aniversários fossem distribuídos de maneira uniforme no ano. Temos 92 jogadores e queremos saber a chance de, distribuindo aleatoriamente no ano, ter uma diferença de 30 nascimentos entre os dois semestres, sendo o primeiro semestre o favorecido. Calculando com cuidado, essa probabilidade não passa do valor 0,08%, extremamente baixa, ela precisa de uma explicação.
Antes que os astrólogos saiam em defesa de alguma correlação entre estrelas e seres humanos, comento a conclusão a que chegaram os estatísticos. Essa predominância de nascimentos em um semestre não ocorre em países europeus, curiosamente, analisei França e Inglaterra e os resultados não são nada impressionantes. Esses três países do sul, Brasil, Argentina e Chile, apresentam sistematicamente jogadores nascidos em um semestre, e a razão disso, muito provavelmente, é o ano letivo.
No mesmo argumento que usou Malcolm Gladwell em seu livro Outliers para explicar jogadores de hóquei, nesses países, as escolas de futebol organizam os alunos de acordo com o ano letivo, e os jogadores profissionais enfrentam peneiras desde cedo para seguir na carreira. Os nascidos no começo do ano são, por isso, os mais velhos de suas turmas e, ao enfrentam peneiras desde crianças, são também os mais fortes e mais rápidos. Os nascidos no primeiro trimestre são quase um ano mais velhos que os nascidos no último, e são selecionados em uma idade em que um ano é muito para o desenvolvimento corporal. Esse resultado é ausente nos times europeus porque as escolas de futebol não seguem um ano específico, algumas tomam o escolar como base e outras o ano de nascimento, não havendo consenso, há equilíbrio na distribuição.
Falta, claro, explicar o caso do Paraguai. Tendo em vista os outros países, o mais natural é supor, ou que o Paraguai é a anomalia estatística, ou que o sistema de escola de futebol e peneira desde muito cedo não é tão rigoroso no Paraguai.
Tudo o que eu acabo de fazer, aviso, consiste em estatística de péssima qualidade. Eu precisaria tomar vergonha na cara, analisar mais jogadores de mais times, informar-me sobre o sistema de avaliação do Paraguai e não me ater a essa tese com muito afinco, ela pode muito bem estar furada. Contudo, os 0,08% chamam a atenção, e confirmam que o estudo do paradoxo do aniversário não pode ser realizado com jogadores de futebol.
Claro que a hipótese feita, a distribuição igual de nascimentos ao redor do ano pela população normal, precisa ser justificada. Redireciono-os ao trabalho desse site, enquanto aponto ao curioso fato do grande número de nascimentos em setembro-agosto, provavelmente resultado das férias de natal, quando a chance de se estar em casa é alta e a programação da televisão cai de qualidade vertiginosamente.
Se o futebol sul-americano já apresenta esse fenômeno, podemos encontrá-lo de forma ainda mais acentuada em esportes cuja dependência da disposição física (e, logo, da idade) seja maior, o hóquei é um bom exemplo. Um grande estudo nesse aspecto foi realizado no Canadá em 1988 e os resultados do estudo são impressionantes, o mês de nascimento parece ter implicação direta no sucesso do jogador. Atualmente, parece que as ligas americanas e canadenses adaptaram um calendário diferente, mais próximo daquele europeu de futebol, e a diferença não é mais gritante.
E esses gráficos nos inspiram a questionar o quanto do sucesso de alguém em uma carreira é fruto de sucesso inicial, de ter se dado bem no começo, gostado, continuado, se esforçado e se dado ainda melhor, um círculo vicioso positivo vindo apenas do fato de ter sido bem sucedido no começo. Extrapolando, podemos nos perguntar se fazemos o que fazemos pelo sucesso inicial, e me pergunto quanto da matemática que faço não vem de uma primeira nota alta na matéria. As coisas talvez tivessem sido diferentes se eu tivesse errado mais questões, se minha professora fosse uma carrasca, se a ponta de meu lápis tivesse quebrado naquela primeira prova ou, quem sabe, se eu tivesse nascido em junho.
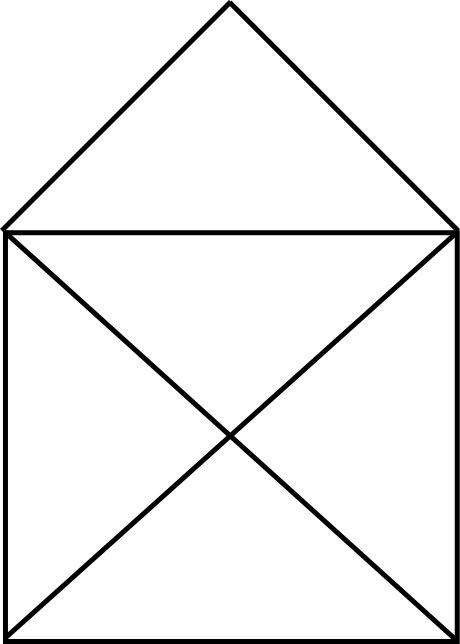 Sendo o objetivo do problema desenhar essa figura sem tirar o lápis do papel e sem repetir os caminhos. Após algumas tentativas, cheguei a um caminho correto, desenhava feliz a casa com o X segundo as regras. Foi então que me foi apresentado uma variante do problema, “mais difícil” segundo aquele que me passou. Fui desafiado a desenhar essa outra figura:
Sendo o objetivo do problema desenhar essa figura sem tirar o lápis do papel e sem repetir os caminhos. Após algumas tentativas, cheguei a um caminho correto, desenhava feliz a casa com o X segundo as regras. Foi então que me foi apresentado uma variante do problema, “mais difícil” segundo aquele que me passou. Fui desafiado a desenhar essa outra figura: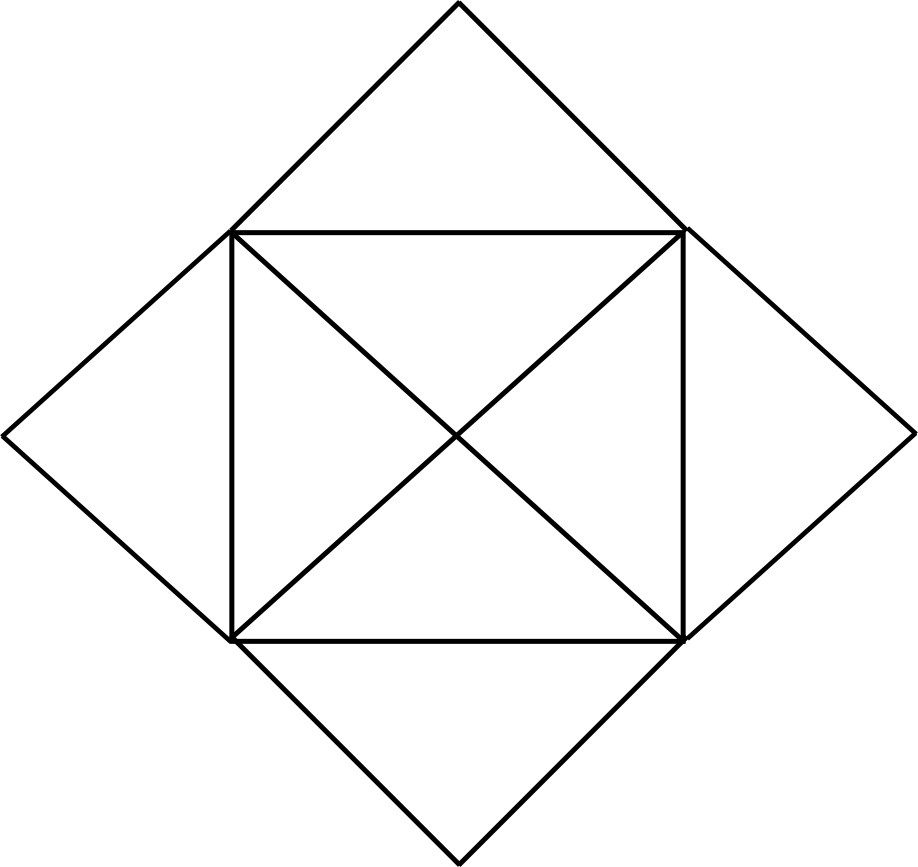 Passei anos tentando, vez ou outra, resolver esse problema. Deixei de dar atenção a ele depois dos treze anos e, aos dezoito, descobri que todas aquelas tentativas fúteis de desenhar essa estranha flor foram justificadas: o problema não tem solução, é impossível encontrar um caminho que desenhe essa figura sem tirar o lápis do papel e sem repetir caminhos.
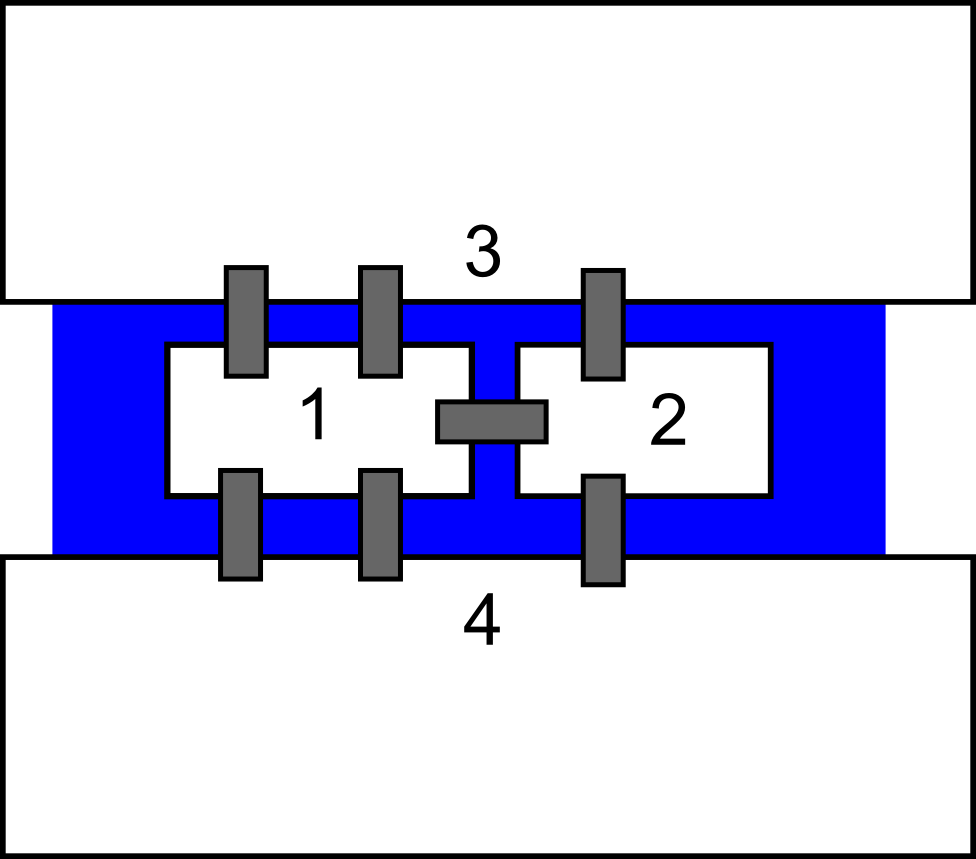
Passei anos tentando, vez ou outra, resolver esse problema. Deixei de dar atenção a ele depois dos treze anos e, aos dezoito, descobri que todas aquelas tentativas fúteis de desenhar essa estranha flor foram justificadas: o problema não tem solução, é impossível encontrar um caminho que desenhe essa figura sem tirar o lápis do papel e sem repetir caminhos. E o desafio era atravessar as sete pontes sem repetir nenhuma. Você pode se divertir tentando, como os habitantes da cidade faziam, mas Euler decidiu pensar no problema de maneira mais profunda. A primeira coisa que fez foi se livrar do que estava sobrando: prédios, ilhas, estradas, apenas as pontes importavam:
E o desafio era atravessar as sete pontes sem repetir nenhuma. Você pode se divertir tentando, como os habitantes da cidade faziam, mas Euler decidiu pensar no problema de maneira mais profunda. A primeira coisa que fez foi se livrar do que estava sobrando: prédios, ilhas, estradas, apenas as pontes importavam: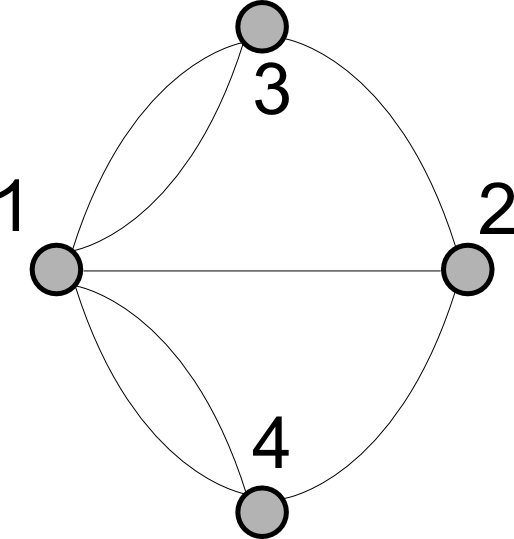 A vantagem desse formato, minimalista ao extremo, é nos permitir focarmos apenas no que realmente importa. E esse foi o raciocínio de Euler: quero atravessar todas essas linhas sem jamais repetir nenhuma. Rapidamente, ele notou que, para não repetir linhas, todo ponto a que ele chegasse deveria permitir uma saída, exceto, claro, pelos pontos inicial e final. Ou seja, para todo o ponto, exceto os de começo e fim, cada entrada deve possuir uma saída correspondente: ele deve possuir um número par de conexões. Se ele possui um número ímpar, digamos, 3; eu entrarei nele, sairei dele e, na próxima entrada, não terei como sair, eu travei e, ao menos que ele seja meu ponto final, perdi o jogo.
A vantagem desse formato, minimalista ao extremo, é nos permitir focarmos apenas no que realmente importa. E esse foi o raciocínio de Euler: quero atravessar todas essas linhas sem jamais repetir nenhuma. Rapidamente, ele notou que, para não repetir linhas, todo ponto a que ele chegasse deveria permitir uma saída, exceto, claro, pelos pontos inicial e final. Ou seja, para todo o ponto, exceto os de começo e fim, cada entrada deve possuir uma saída correspondente: ele deve possuir um número par de conexões. Se ele possui um número ímpar, digamos, 3; eu entrarei nele, sairei dele e, na próxima entrada, não terei como sair, eu travei e, ao menos que ele seja meu ponto final, perdi o jogo.