Certa vez, um amigo me contava de sua saída do trabalho, na sede da Peugeot. Todo dia, ele era confrontado com a escolha entre dois ônibus para chegar a seu destino, cada um saindo de um ponto diferente de sua empresa, mas ambos passando por sua casa. O primeiro, mais moderno, confortável, equipado e vazio, passava uma vez a cada quinze minutos. O segundo, mais rampeiro e cheio, passava a cada cinco minutos. No dilema entre conforto e pressa, meu amigo estabeleceu um critério: olharia o ponto do ônibus moderno e, se já houvesse alguém esperando, julgaria que valia a pena esperar, pois um tempo razoável já haveria se passado. Se não houvesse ninguém, voltaria nos sacolejos do outro ônibus.
Ao comentar seu critério com um colega de profissão, foi-lhe dito que era absurdo, pois a pessoa poderia ter acabado de chegar, que esse critério era o mesmo que nada. Ele propôs o problema a nosso grupo de amigos, e eu instintivamente achei um bom critério, se não pelo bom senso da explicação, por um instinto físico de considerar que haver uma pessoa representava ganho de informação, como se a entropia tivesse diminuído em relação à situação “eu não sei nada sobre o ônibus”, que é o caso original. Mas sem falar de entropia ou o que o valha, eu precisava provar meu ponto, e precisava conversar um pouco sobre como pessoas esperam um ônibus.
Esse post deveria ser simples e rápido, acabou saindo do controle, peço desculpas antecipadas pelo malabarismo de probabilidades, assuntos e variáveis, não consegui fazer mais simples; juro que tentei.
Imaginemos um ponto de ônibus ideal em que passa um ônibus a cada $T$ minutos. No caso de meu amigo, $T=15$ minutos. Suporei que a chance de um passageiro chegar ao ponto para esperar é sempre a mesma em todos os instantes durante esse tempo $T$, ou seja, estou desconsiderando efeitos que possam aumentar ou diminuir drasticamente a chegada de pessoas durante a espera de um ônibus, esse modelo não funciona bem para as 18h da empresa. Suponha que, a cada leva, o ônibus recebe em média $\lambda$ pessoas. Não sei os valores para o caso de meu amigo, mas eu noto que esse número é importante. Se o ônibus recebe a cada quinze minutos em média 10 pessoas, não é trivial saber exatamente o que haver uma pessoa esperando quer dizer; contudo, se ele recebe 50, haver apenas uma indica que ele acabou de passar.
Então temos que a cada $T$ minutos, em média, juntam-se $\lambda$ pessoas no ponto. Suponho que o fluxo de pessoas para o ponto seja constante, e me pergunto: qual a chance do ônibus receber $\lambda-1$ pessoas? Ou $\lambda+1$? Ou $\lambda/2$? Tais perguntas não são simples, mas são todas respondidas pelo que chamamos de distribuição de Poisson.
Tenho um intervalo de $T$ minutos entre um ônibus e outro, sei que as pessoas podem chegar a qualquer momento durante esses minutos. Minha única informação é que a média de pessoas que chegam ao final de $T$ minutos é $\lambda$. Para estudar essa estatística, vou usar um truque matemático para modelizar a situação como um processo binomial. O truque é dividir meu intervalo de 15 minutos em 900 intervalos de um segundo. A escolha do segundo é para fins didáticos, o correto seria escolher dividir 15 minutos no maior número de intervalos possíveis, cada um com uma duração cada vez menor. Vou supor que o ônibus encontra, em média, $\lambda=20$ pessoas no ponto. Assim, posso dizer que a chance de uma pessoa chegar em um dado segundo é $20/900$. A razão para essa divisão em 900 segundos é que essa afirmação só é possível se duas pessoas não puderem chegar no exato mesmo segundo. Se eu tivesse escolhido dividir meu intervalo em minutos, não faria sentido dizer que a chance de uma pessoa chegar em um minuto é $20/15$, essa chance é maior que um! Seria como cometer o erro de dizer que, se a chance de tirar cara ao tirar uma moeda é de 50%, então em três lançamentos a chance é de 150%!
Essa divisão nos intervalos bem pequenos serve para eu transformar a chegada de pessoas no ônibus em um processo de zeros e uns. Cada segundo receberá um número, 0 se nenhuma pessoa chegou nesse segundo, 1 se alguém chegou nesse segundo. A cada segundo, portanto, estará associada uma probabilidade $p$ de chegar uma pessoa. O que sabemos é que, se o número de segundos é $N$, então $Np=\lambda$, o número médio de pessoas será a probabilidade de uma chegar em um segundo vezes o número total de segundos. Isso só é possível porque a chegadas das pessoas não possui correlação e porque ninguém pode chegar no mesmo segundo que outra pessoa.
Para calcular a probabilidade, ao final de $N$ segundos, de se obter $k$ pessoas no ponto, preciso pensar que aqueles $N$ segundos ganharam um número $k$ de uns e um número $N-k$ de zeros. Ou seja, se quero saber a chance de 10 pessoas chegarem no ponto no final de 900 segundos, terei que dentre esses 900 segundos 10 deles receberam pessoas e 890 não receberam. A probabilidade de 10 segundos específicos receberem pessoas é de $p^{10}(1-p)^{890}$, pois aqueles dez devem receber e os 890 restantes devem não receber pessoas. Mas como não sei quais segundos receberam, devo considerar todas as combinações possíveis de segundos que receberam essas pessoas, devo multiplicar esse valor por $\binom{900}{10}$. A probabilidade $p$ pode ser determinada dividindo o número médio de pessoas 20 pelos 900 segundos, e teremos a probabilidade de encontrar 10 pessoas no ponto de ônibus: $P(k=10)=\binom{900}{10}\left(2/90\right)^{10}\left(1-2/90\right)^{890}$, um valor um pouco maior que 0,55%.
Esse raciocínio, contudo, tem problemas. Em primeiro lugar, eu deveria, por honestidade intelectual, dividir o intervalo em bem mais que 900 segundos, deveria usar 900.000 milissegundos para garantir que ninguém mesmo chegará no mesmo intervalo e poder usar essas contas com segurança. Mas se os cálculos já ficaram feios com 900, afinal, o binomial envolve fatoriais desse valor, imagine fazer contas com 900.000 fatorial! Esse caminho é impraticável, e por isso Simeon-Denis Poisson vem a nosso socorro. Através de uma aproximação malandra ((conhecida como aproximação de Stirling)), Poisson nos diz que:
\[ \binom{N}{k}\left(p\right)^{k}\left(1-p\right)^{N-k}\underbrace{\longrightarrow}_{N\to \infty} \frac{(Np)^k}{k!}e^{-Np}\]
O que é muito oportuno, porque sabemos que $Np$ é a média de pessoas que está no ponto após os quinze minutos, ela é igual a $\lambda$! Essa aproximação é cada vez melhor se o número de divisões do intervalo de tempo é maior, e eu quero mesmo é que isso seja grande, quanto maior for, menor é a chance de duas pessoas chegarem no mesmo intervalo de tempo. Então eu mando $N$ logo para infinito e digo que que a probabilidade de se encontrar $k$ pessoas no ponto de ônibus depois de quinze minutos (lembro que $T=15$ nesse caso) é:
\[P(k|T)=\frac{\lambda^k}{k!}e^{-\lambda},\]
onde $\lambda$ é a média de pessoas que encontro no ponto de ônibus no final dos quinze minutos de espera, essa é conhecida como a distribuição de Poisson. Saberei, com isso, a probabilidade de encontrar um número $k$ de pessoas ao final de cada espera de 15 minutos:
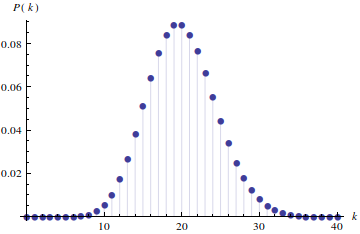
Isso ainda não resolve meu problema, mas ajuda bastante, como veremos. Sei qual a probabilidade de encontrar $k$ pessoas após 15 minutos, pergunto então: qual a probabilidade de encontrar $k$ pessoas após $t$ minutos? Se com os 15 minutos bastou usar a distribuição de Poisson com parâmetro igual à média de pessoas que chegam em 15 minutos, com os $t$ minutos bastaria usar a mesma distribuição, trocando a média dos 15 pela média dos $t$. Como a taxa de chegada dos passageiros no ponto é constante, a média evolui linearmente de 0 a $\lambda$, ou seja, a média $\lambda(t)$ de passageiros no ponto em um tempo $t$ é $\frac{\lambda}{T}t=\mu t$, onde $\mu$ é a taxa de chegada das pessoas. A probabilidade de encontrar $k$ pessoas no ponto no instante $t$ será:
\[ P(k|t) = \frac{(\mu.t)^k}{k!}e^{-\mu t}\]
Essa distribuição dependente do tempo é conhecida como processo de Poisson, e descreve muito bem a chegada de pessoas em um ponto de ônibus. Temos agora exatamente a probabilidade de encontrar um número qualquer de pessoas em um instante qualquer de espera, queremos saber, então, se aquele critério de meu amigo presta a alguma coisa. Para isso, precisamos conversar um pouco sobre probabilidade condicional, e sobre como calcular probabilidades quando já sabemos algo sobre o processo.
O que quero é a chance de terem se passado $t$ minutos uma vez que há $k$ pessoas no ponto. Vou chamar essa chance de $P(t|k)$. O que tenho até agora é a probabilidade de encontrar $k$ pessoas uma vez que se passaram $t$ minutos, ou seja, tenho $P(k|t)$. Essas probabilidades parecem similares, mas possuem sentidos completamente diferentes; uma é a chance de chover se há nuvens, outra é a chance de haver nuvens se chove. Se quero de uma obter a outra, preciso usar o teorema de Bayes:
\[P(t|k) = \frac{P(k|t) P(t)}{P(k)},\]
onde $P(k)$ é a probabilidade de encontrar $k$ pessoas no ponto sem qualquer informação sobre o horário, e $P(t)$ é a probabilidade de estarmos no instante $t$.
Há um problema grave na definição de $P(t)$, pois a chance real de estarmos no instante $t$ é nula, porque $t$ é um número real e a chance de estarmos exatamente às 13h43m10s325ms901μs… é zero, não é possível atribuir a probabilidade de se obter um número real no meio da reta real. Mas podemos pensar na chance de estar entre dois horários, entre o primeiro e o segundo minuto, por exemplo. E essa chance, naturalmente é igual para todos os minutos, não temos razão para, chegando ao ponto de ônibus, supor que ele passou faz 3 minutos, ou 5, sem olhar para os passageiros que estão no ponto. Meu amigo, aliás, quer saber se há alguma diferença entre $P(t|k)$ (probabilidade de estar em $t$ sabendo $k$) e $P(t)$ (probabilidade de estar em $t$ sem saber nada sobre $k$). Se o tempo total possível de espera é de $T$, a chance de estarmos em um intervalo de tempo de tamanho $\Delta t$ é igual para todo intervalo: $\frac{\Delta t}{T}$. Para o propósito de nosso problema, vale a pena pegar intervalos muito pequenos de tempo. Ao escrevermos $P(t)$ queremos, na verdade, dizer “probabilidade de estar em um intervalo de tempo $dt$ muito pequeno centrado em $t$”, ou seja, $P(t)=\frac{dt}{T}$.
Calcular $P(k)$, por outro lado, não é tão simples. Devemos pegar a chance de encontrar $k$ pessoas no ponto no instante $t$ ( $P(k|T)$ ), multiplicar pela chance de estar em $t$ ( $P(t)$ ) e somar em todos os $t$’s possíveis. Essa é a única maneira de calcular a chance de ter $k$ sem saber nada sobre $t$, é somar a chance de estar em qualquer $t$ possível. Matematicamente, isso é fazer a integral: $\int_0^T P(k|T)\frac{dt}{T}$. Trabalhando um pouco, chegamos a:
\[ \int_0^T \frac{(\mu.t)^k}{k!}e^{-\mu t}\frac{dt}{T} = 1-\frac{\Gamma(1+k,T\mu)}{T\mu k!}\]
Chamamos essa função estranha do lado direito de função Gamma incompleta, ela é apenas um jeito elegante de escrever $\Gamma(s,x) = \int_x^{\infty} t^{s-1}\,e^{-t}\,{\rm d}t$, uma integral que não sabemos fazer, mas que numericamente sai com tranquilidade.
Depois de muito malabarismo, chegamos à resposta mais completa ao dilema de meu amigo. Dadas as seguintes hipóteses:
- O ônibus passa uma vez a cada $T$ minutos.
- O ônibus encontra, a cada vez, em média, $\lambda$ pessoas esperando no ponto.
- A taxa de chegada de pessoas no ponto de ônibus é constante, igual a $\mu=\lambda/T$.
- Ninguém corre para pegar o ônibus (hipótese que provavelmente torna o modelo inútil).
Então a densidade de probabilidade $P(t|k)$ é:
\[ P(t|k) =\frac{P(k|t)P(t)}{P(k)}=\frac{\frac{(\mu.t)^k}{k!}e^{-\mu t}\frac{1}{T}}{1-\frac{\Gamma(1+k,T\mu)}{T\mu k!}},\]
Essa é a densidade de probabilidade. Para descobrir qual a chance de que o último ônibus tenha passado há $\tau$ minutos, você deve integrar essa expressão de 0 a $\tau$. Felizmente temos o Mathematica para isso. Assim, ao encontrar $k$ pessoas no ponto, a chance de que o ônibus tenha passado há pelo menos $\tau$ minutos é:
\[ P(\tau)=\int_0^\tau P(t|k)dt=\int_0^\tau \frac{P(k|t)P(t)}{P(k)}=\frac{\int_0^\tau\frac{(\mu.t)^k}{k!}e^{-\mu t}\frac{dt}{T}}{1-\frac{\Gamma(1+k,T\mu)}{T\mu k!}}=\frac{\Gamma(1+k,\tau\mu)-\Gamma(1+k,T\mu)}{1-\Gamma(1+k,T\mu)}\]
Tomemos valores realistas. Sabemos que $T=15$. Vamos supor que a cada chegada, em média, o ônibus encontra $N=6$ pessoas. Para que meu amigo fique feliz com o post, apresento o resultado para encontrando duas pessoas ($k=2$), uma pessoa ($k=1$), não vendo ninguém no ponto ($k=0$) e não sabendo absolutamente nada sobre o ponto ($k=?$), essa é a probabilidade de que o ônibus tenha passado há pelo menos $\tau$ minutos:
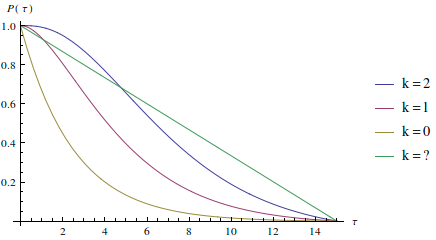 É claro que a chance é alta de que o ônibus tenha passado há ao menos um minuto, bem como é bem difícil que ele tenha passado há 14 minutos ou mais. Com isso, fechamos o problema. Percebemos alguns aspectos importantes do critério de meu amigo. Primeiro, ele não é equivalente a não saber nada sobre o ponto, as distribuições são bem diferentes. Segundo, observar uma única pessoa, sendo a média de embarque seis, indica que é mais provável que o ônibus tenha passado faz quatro minutos ou menos, você conta ainda com uma espera de uns bons onze minutos. Pelo número de pessoas que encontra no ponto, é capaz de, negociando com sua espera, decidir se se rende ao desconforto ou se volta paciente e confortavelmente para sua casa.
É claro que a chance é alta de que o ônibus tenha passado há ao menos um minuto, bem como é bem difícil que ele tenha passado há 14 minutos ou mais. Com isso, fechamos o problema. Percebemos alguns aspectos importantes do critério de meu amigo. Primeiro, ele não é equivalente a não saber nada sobre o ponto, as distribuições são bem diferentes. Segundo, observar uma única pessoa, sendo a média de embarque seis, indica que é mais provável que o ônibus tenha passado faz quatro minutos ou menos, você conta ainda com uma espera de uns bons onze minutos. Pelo número de pessoas que encontra no ponto, é capaz de, negociando com sua espera, decidir se se rende ao desconforto ou se volta paciente e confortavelmente para sua casa.
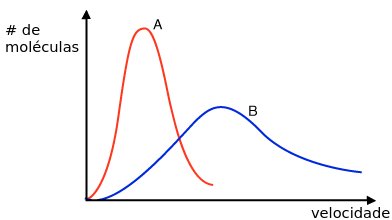 Nesse gráfico, a distribuição A significa um gás em temperatura menor, enquanto o B representa um mais quente. É fácil ver que no B haverá mais moléculas com mais velocidade, e no A as moléculas estarão mais concentradas em regiões de velocidade mais baixa. Maxwell descobriu isso usando apenas matemática, um feito impressionante em uma época em que a própria existência dos átomos era questionada. Como de costume, ele tinha razão, ainda que nenhuma verificação disso fosse possível na época. Maxwell deduziu o que seria a distribuição de velocidades de partículas se movendo em direções aleatórias e cujas colisões seriam como as de bolas de bilhar; sendo esse gráfico o resultado da colisão de muitas, muitas dessas partículas.
Nesse gráfico, a distribuição A significa um gás em temperatura menor, enquanto o B representa um mais quente. É fácil ver que no B haverá mais moléculas com mais velocidade, e no A as moléculas estarão mais concentradas em regiões de velocidade mais baixa. Maxwell descobriu isso usando apenas matemática, um feito impressionante em uma época em que a própria existência dos átomos era questionada. Como de costume, ele tinha razão, ainda que nenhuma verificação disso fosse possível na época. Maxwell deduziu o que seria a distribuição de velocidades de partículas se movendo em direções aleatórias e cujas colisões seriam como as de bolas de bilhar; sendo esse gráfico o resultado da colisão de muitas, muitas dessas partículas.