Esse post foi escrito a um grande amigo, quando este ano passado prestou o curso de engenharia química e passou. Apesar de nossas rivalidades, engenharia química é a fusão de duas rixas velhas de estudantes da graduação de física, aprecio e admiro o trabalhos desses cientistas.
A meu engenheiro químico favorito.
Como você deve saber, físicos e químicos possuem aquela rivalidade saudável entre duas ciências bem resolvidas. Ambas são torturadas durante o ensino médio, ambas são detestadas por todos os seus amigos menos eu e ambas, durante sua aprendizagem até a faculdade, contam muitas mentiras. Certo, admito que mentira é uma palavra forte, seria mais educado dizer que os ensinamentos são incompletos e imperfeitos, porque quem tem problemas com U=R.I dificilmente conseguirá apreciar a quântica. Não porque ela é difícil, mas porque ela exige base, maturidade científica, sobriedade no raciocínio; nenhuma matéria na física é realmente difícil se você possui esses três elementos ((Exceto mecânica dos fluidos. Mecflu é só crueldade.)) .
E tem algumas coisas que eu queria compartilhar com você nesse ingresso de faculdade, coisas que demorei a aprender e entender, e que mudaram a maneira como vejo o mundo. Elas envolvem os tijolos de suas futuras construções teóricas: os átomos. Química é a arte de explicar o que acontece quando dois átomos ou mais se juntam, dessa pergunta saem tantas grandes realizações do século XX: o plástico, o poliéster, tantos medicamentos, cosméticos e cada pixel da tela de seu computador. Química estuda $n$ átomos juntos, formando moléculas, compostos, colóides, sempre com $n>2$. Isso porque se $n=1$, a bola ainda está no território da física.
Confesso que isso não é completamente verdade, porque o átomo de Hélio, por exemplo, já representa um desafio hercúleo para um físico calcular, sendo necessários os melhores computadores atuais para conseguir boas respostas para a perguntas que fazemos sobre esse gás nobre. Quem realmente é a prata da casa é o hidrogênio, nosso átomo favorito, pois possui apenas um elétron. Não temos nada contra prótons, eles podem aparecer em números grandes, nosso problema é com os elétrons. Neste breve texto, vou comentar algumas coisas legais que conheço dos três elementos do átomo de hidrogênio: o elétron, o nêutron e o próton. Com isso em mente, você deixa sua imaginação livre para formar quantos compostos, moléculas, redes, estruturas, plásticos e remédios você quiser.
Como você imagina um átomo? Essa é a primeira imagem que o Google nos dá quando buscamos “átomo de hidrogênio”:
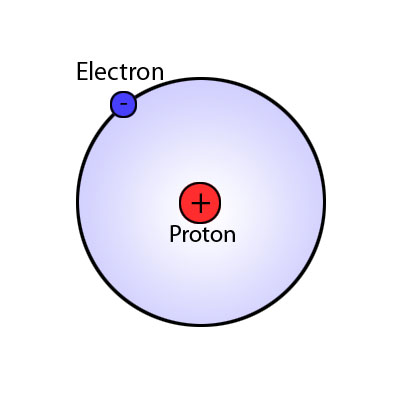
Essa é a visão tradicional do átomo, aquela do ensino médio. Quando você aprende um pouco mais de física ou química, descobre que nada é parecido com esse pequeno sistema planetário que nosso professor desenha na lousa, que a palavra “camadas” faz bem menos sentido do que você imagina. Vou tentar construir aos poucos a ideia do átomo de hidrogênio, começando pelo elétron no post de hoje.
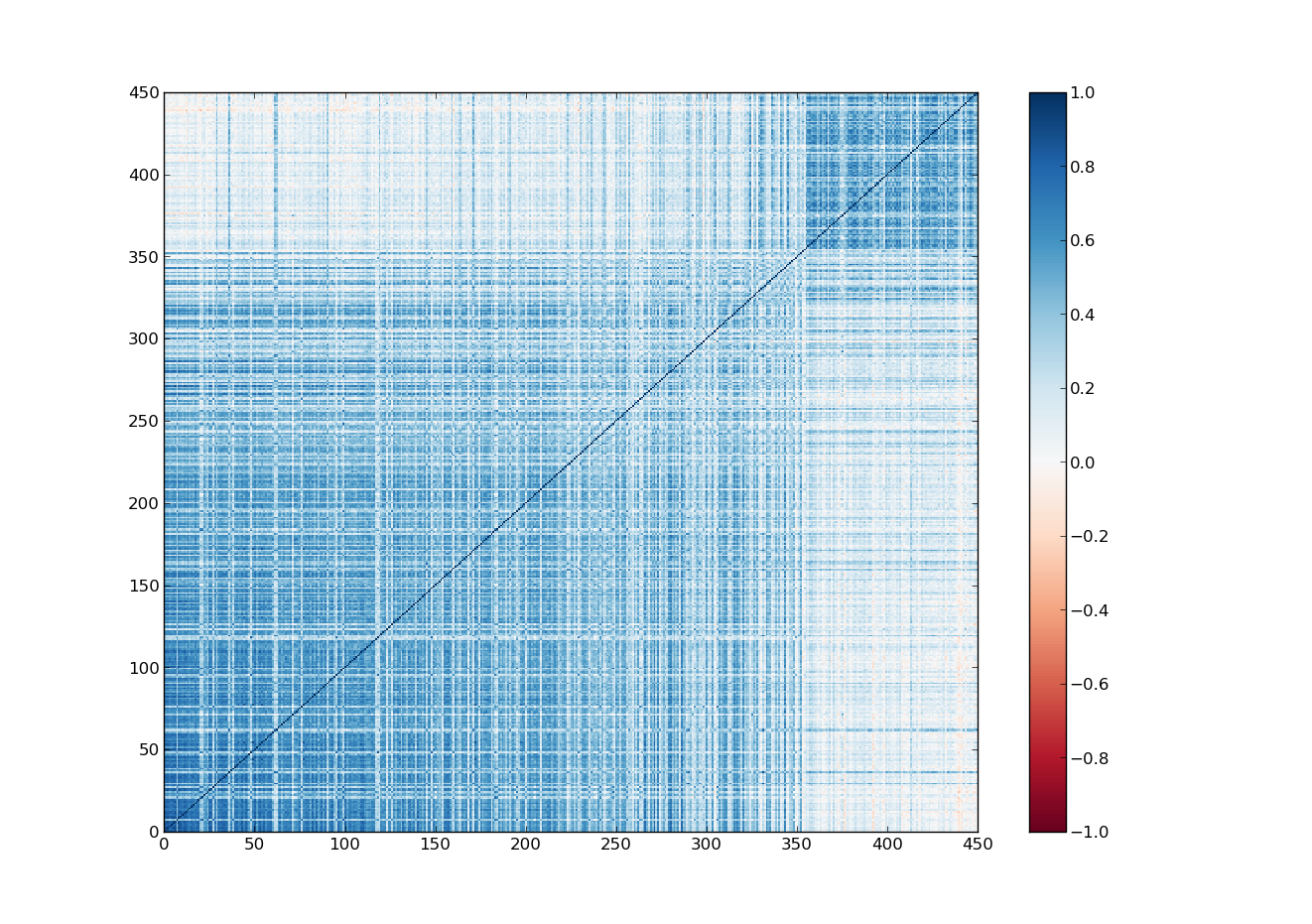
Por enquanto, esqueça tudo o que sabe do átomo. Imagine apenas um ponto central, que chamamos de núcleo. Nele moram prótons e nêutrons, mas vamos ignorar isso por enquanto. Em volta desse núcleo há uma carga negativa, que chamamos de elétron. Sabemos que ele está lá porque somos capazes de medi-lo, podemos jogar um fóton (que é, grosso modo, um pouco de luz) e veremos que o fóton é rebatido em algum ponto em torno do núcleo. Esse ponto era a posição do elétron quando foi atingido. Como de costume, e mediante protestos, o elétron será azul e o próton vermelho.
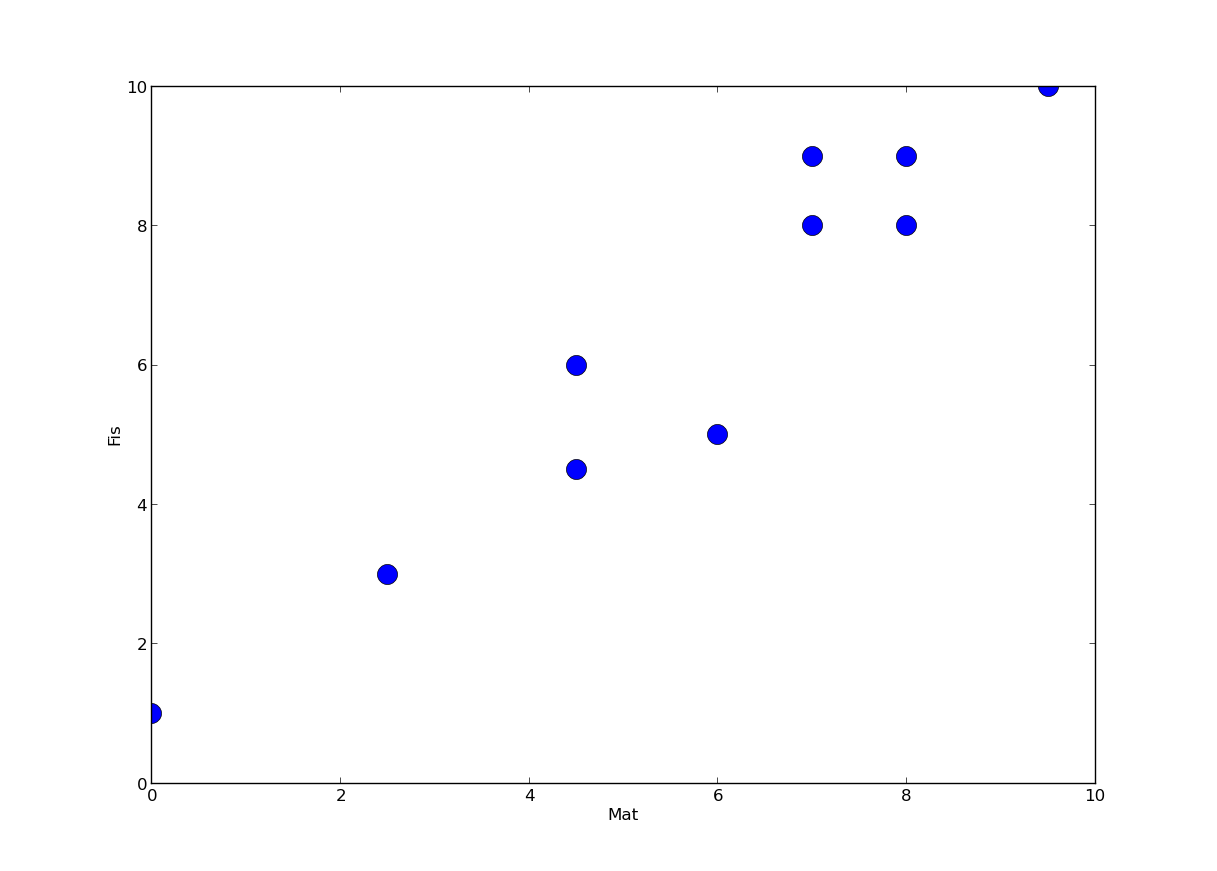
 Eu posso me perguntar se existe a noção de órbita do elétron, posso querer saber por onde ele passa e para onde vai. Eu efetuo 100 medidas da posição do elétron, terei algo parecido com isso:
Eu posso me perguntar se existe a noção de órbita do elétron, posso querer saber por onde ele passa e para onde vai. Eu efetuo 100 medidas da posição do elétron, terei algo parecido com isso:
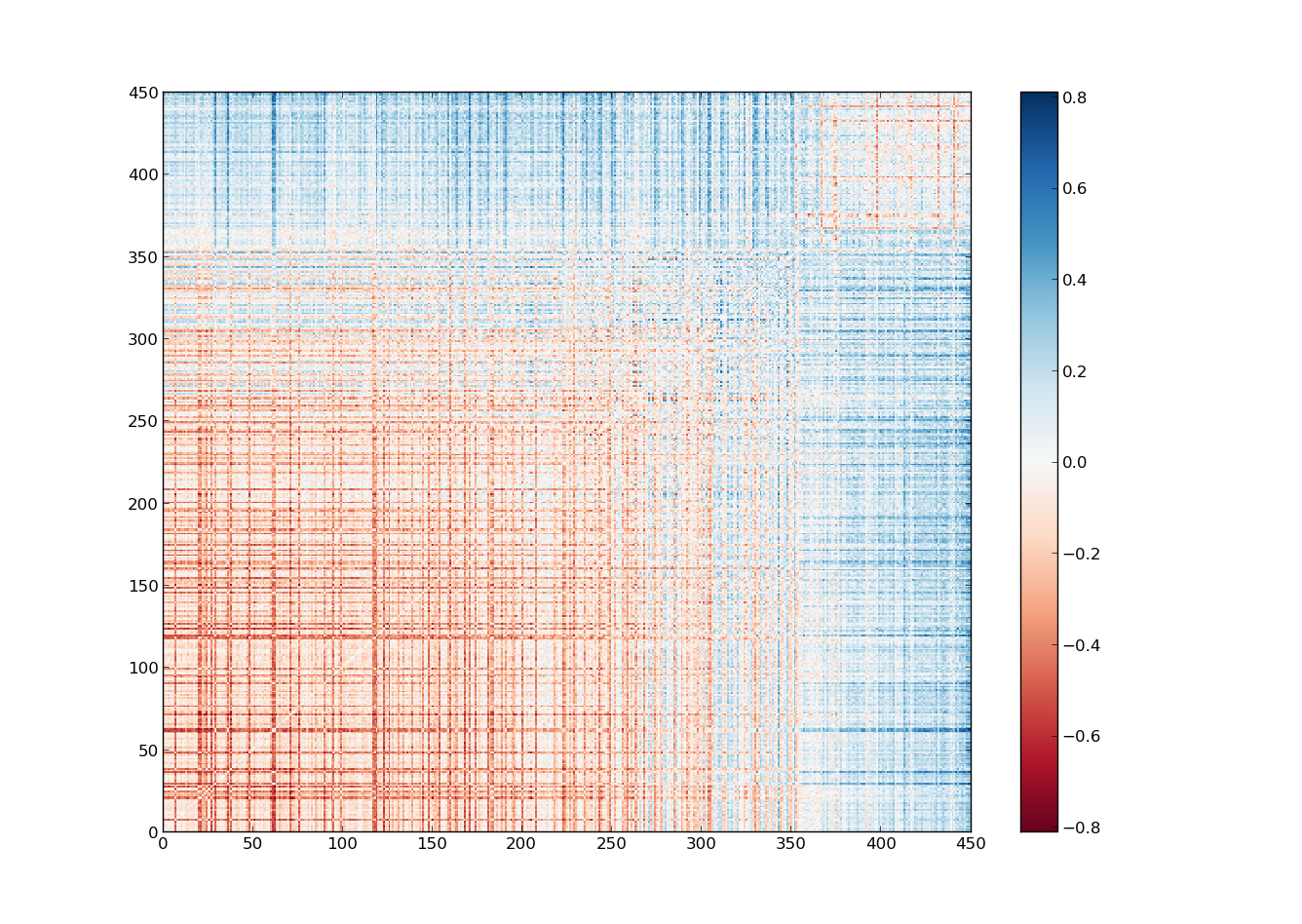
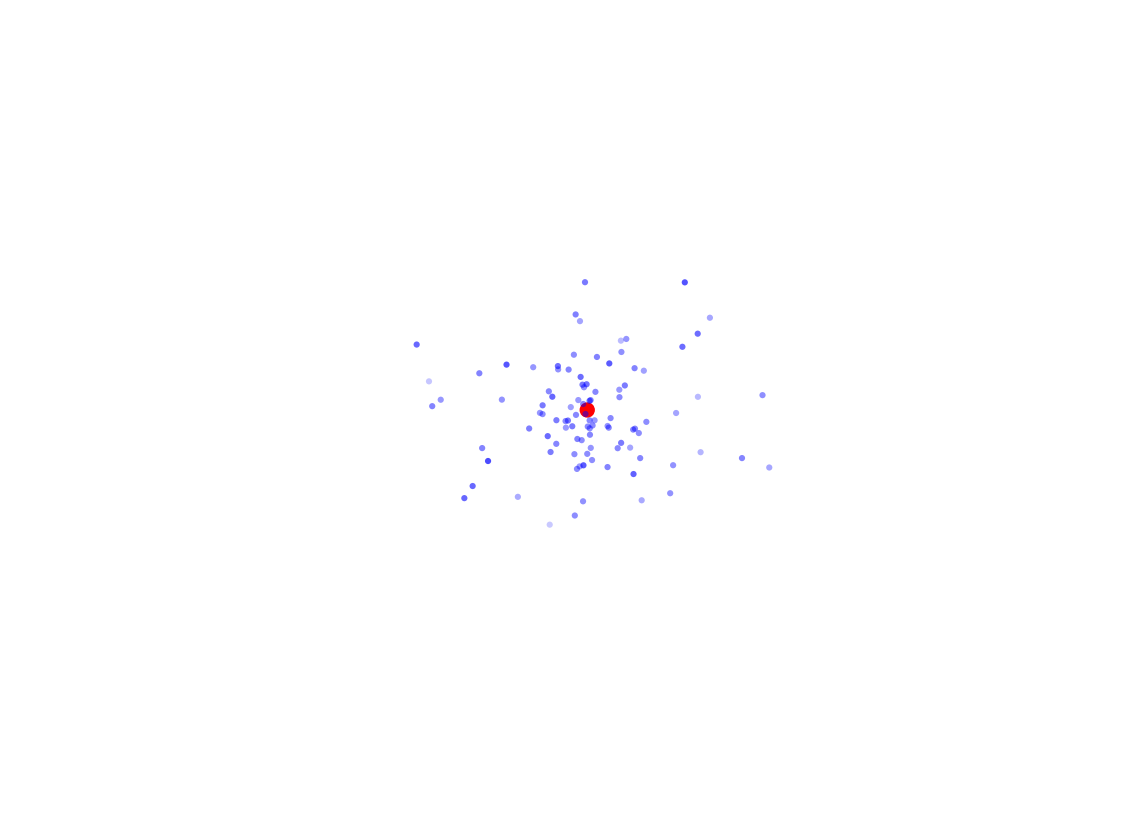 Os pontos azuis são agora medidas do mesmo elétron, em momentos diferentes. Como é fácil perceber, fica bem difícil falar em órbita, e fica ainda mais difícil acreditar naquele desenho dos círculos perfeitos. Para garantir, vamos tomar 1000 medidas da posição do elétron:
Os pontos azuis são agora medidas do mesmo elétron, em momentos diferentes. Como é fácil perceber, fica bem difícil falar em órbita, e fica ainda mais difícil acreditar naquele desenho dos círculos perfeitos. Para garantir, vamos tomar 1000 medidas da posição do elétron:
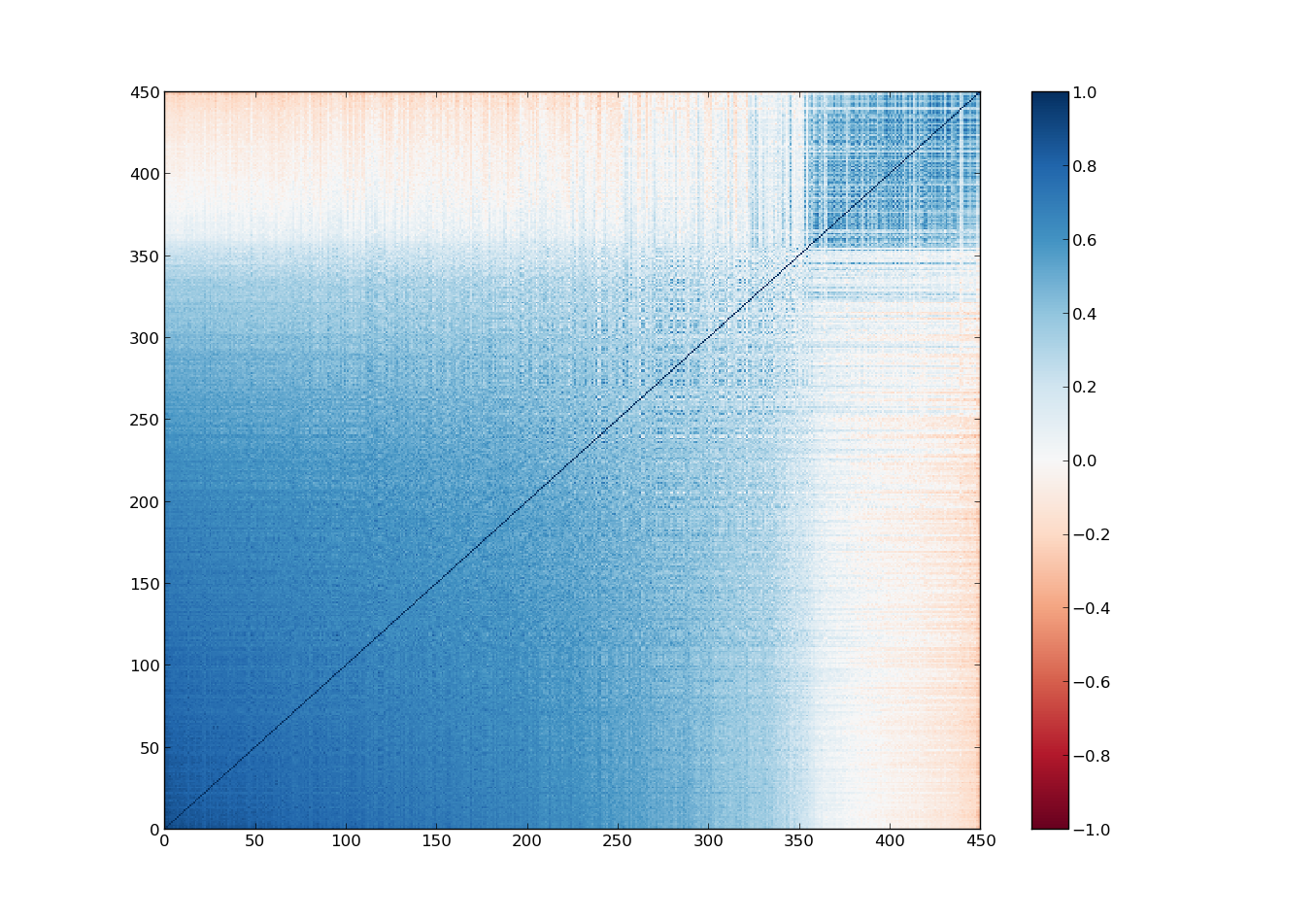
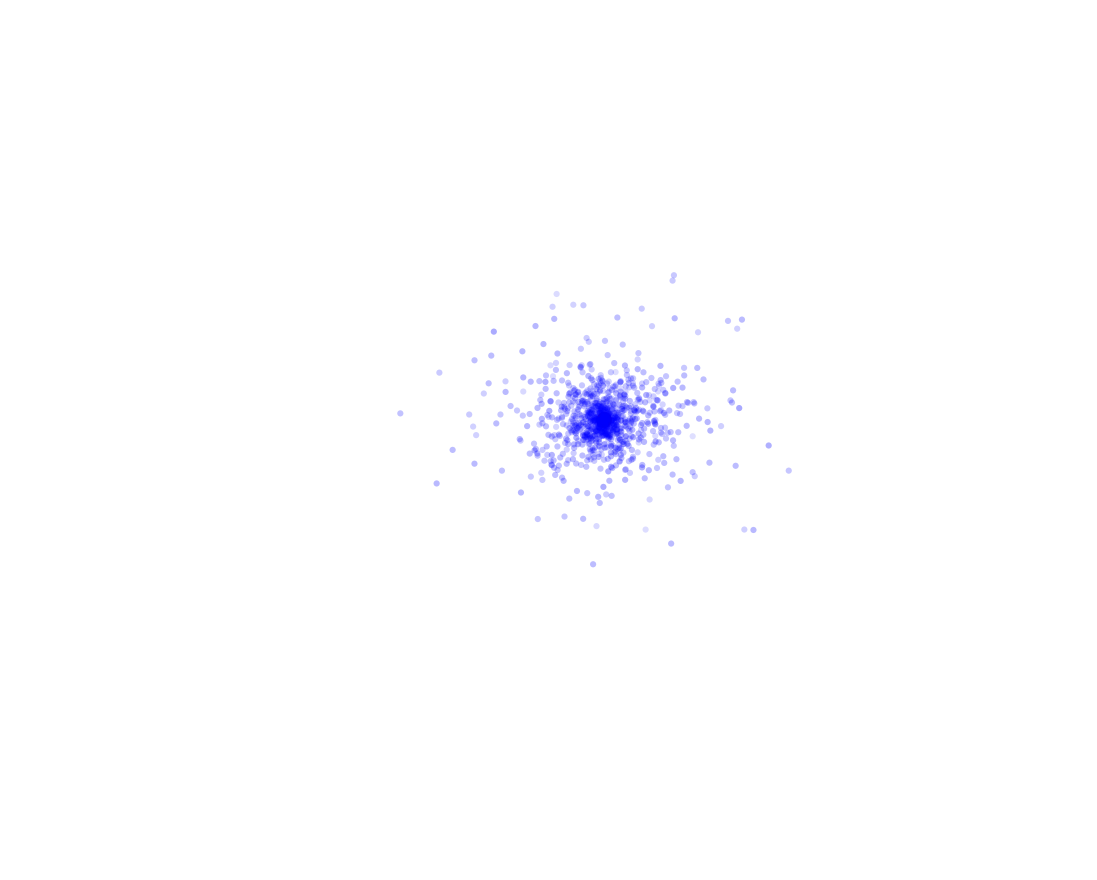 Isso é o registro da posição do mesmo elétron em vários momentos diferentes, o que nos obriga a repensar bastante sobre o que sabíamos do elétron. Por esse e alguns outros motivos, passamos a algumas noções mais radicais sobre as partículas elementares: A noção de trajetória já era. Não apenas não podemos dizer que ele gira em círculos, não podemos nem dizer que ele gira, nem podemos falar de sua trajetória, pois nem sabemos se existe uma.
Isso é o registro da posição do mesmo elétron em vários momentos diferentes, o que nos obriga a repensar bastante sobre o que sabíamos do elétron. Por esse e alguns outros motivos, passamos a algumas noções mais radicais sobre as partículas elementares: A noção de trajetória já era. Não apenas não podemos dizer que ele gira em círculos, não podemos nem dizer que ele gira, nem podemos falar de sua trajetória, pois nem sabemos se existe uma.
Você pode objetar dizendo: mas é claro que existe uma trajetória, ela só é muito complexa. E por mais que isso pareça razoável e você queira que seja verdade, nenhuma evidência que temos aponta para esse lado. O máximo que podemos dizer do elétron é que ele tem uma probabilidade maior de ser medido próximo do núcleo que longe do núcleo, afinal, você percebe que a maior parte das medições caiu na zona vizinha ao próton. Podemos descrever qual a probabilidade de ele ser encontrado a uma dada distância do centro.
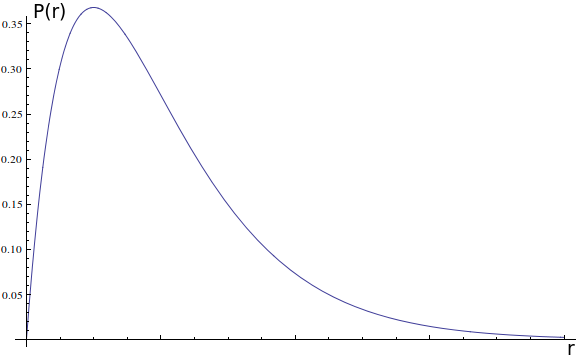 Essa figura é uma densidade de probabilidade, não é difícil de ler. Se você quer saber qual a chance do elétron estar em uma região entre $r_a$ e $r_b$, basta calcular a área da curva entre esses dois pontos e essa será a probabilidade.
Essa figura é uma densidade de probabilidade, não é difícil de ler. Se você quer saber qual a chance do elétron estar em uma região entre $r_a$ e $r_b$, basta calcular a área da curva entre esses dois pontos e essa será a probabilidade.
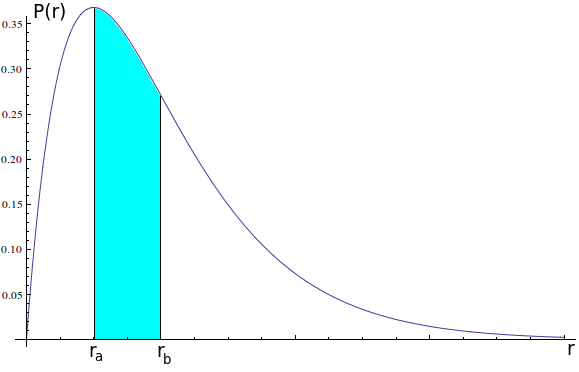 Ou seja, a chance do elétron estar, em uma medida, entre $r_a$ e $r_b$ é a área da região azul. Notamos que há um pico nessa probabilidade, os valores perto desse pico são os mais prováveis. O raio que possui a maior probabilidade é chamado raio de Bohr, e, em muitas aproximações, o átomo pode ser considerado uma esfera maciça cujo raio é o raio de Bohr.
Ou seja, a chance do elétron estar, em uma medida, entre $r_a$ e $r_b$ é a área da região azul. Notamos que há um pico nessa probabilidade, os valores perto desse pico são os mais prováveis. O raio que possui a maior probabilidade é chamado raio de Bohr, e, em muitas aproximações, o átomo pode ser considerado uma esfera maciça cujo raio é o raio de Bohr.
O mais agoniante nisso tudo é que essa densidade de probabilidade é toda a informação que temos sobre a posição do elétron, e a física, como é escrita hoje, parece nos indicar que esse é o máximo de informação que teremos nessa área da vida do elétron. O desenho do ensino é bem intencionado, porque seria difícil ensinar a alunos do ensino fundamental e médio (e também seria difícil cobrar em prova) que há muito que não sabemos e não poderemos saber, e que isso não é um problema. A ciência não é feita de verdades absolutas, mas de verdades em construção, modelos que se aproximam cada vez mais da realidade. Na física quântica, podemos apenas encontrar as probabilidades das partículas estarem onde as medimos, e isso já é bastante informação a respeito delas.
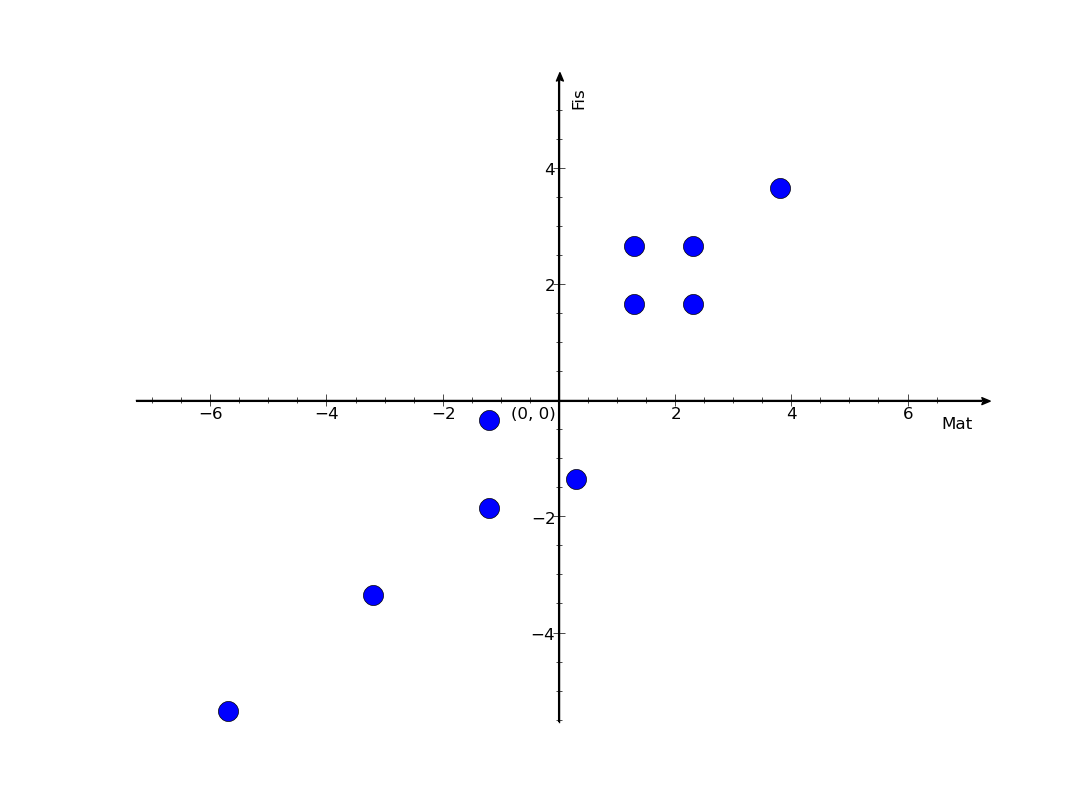
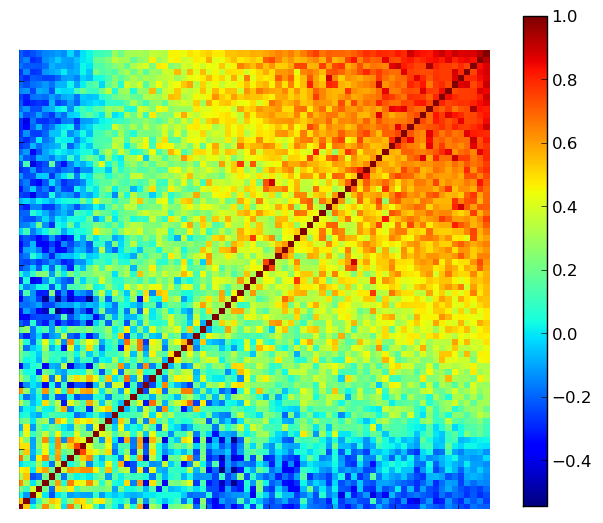
Se você der mais energia a esse elétron, dizemos que ele mudará de camada. Em um primeiro momento, ele absorve uma quantidade precisa de energia, nem mais, nem menos, e passa a ser medido em uma região idêntica à anterior, mas com a possibilidade de ir mais longe. É meramente um aumento no raio de Bohr, chamamos essa situação de um elétron na camada 2s. Se você dá mais energia ao elétron, ele começa a se comportar de um jeito bem diferente. A próxima camada, chamada 2p, é dramaticamente diferente. Se eu medisse um mesmo elétron em torno do átomo de hidrogênio mil vezes, e se esse elétron estivesse na camada 2p, esse seria um resultado possível de minha medida:
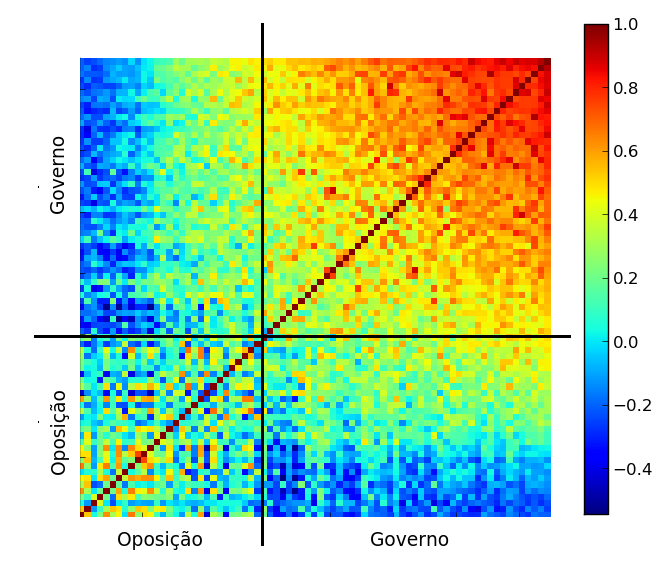
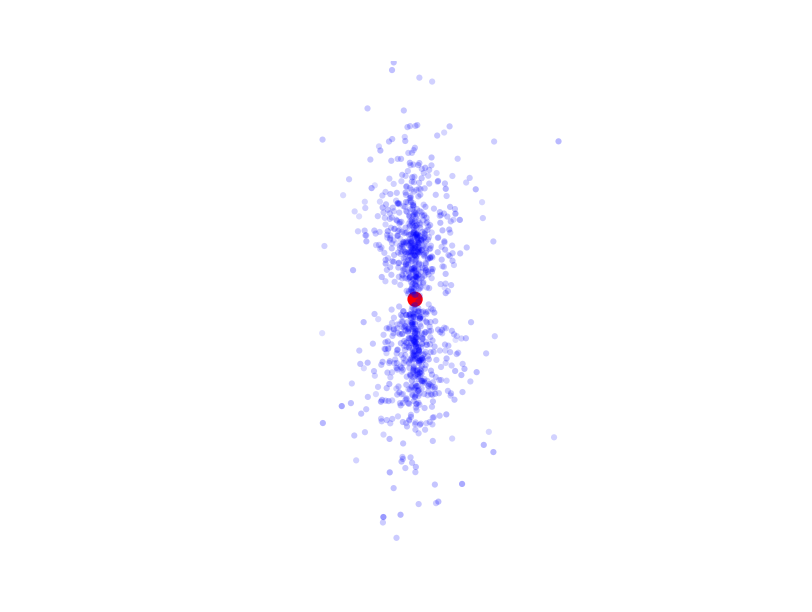 Note que eu continuo tendo uma preferência a estar perto do núcleo, mas noto que o elétron parece gostar mais de estar ou do lado de cima ou do lado de baixo, é quase impossível encontrar elétrons no anel lateral do átomo! Volte àquele desenho inicial e reflita sobre como ele é problemático. Os elétrons não giram em torno do átomo, a noção de trajetória nem existe, conseguimos apenas definir essas formas de probabilidade de medir o elétron em um lugar ou outro. Essa forma é a superfície na qual é igualmente provável encontrar um elétron. No caso das camadas 1s e 2s, essa superfície é uma esfera. A chance de encontrar um elétron afastado de uma distância $a$ do núcleo é a mesma para todos os lados, por isso dizemos que o orbital dessas camadas é uma esfera. No caso da 2p, vemos que essa forma muda, e ela será parecida com isso:
Note que eu continuo tendo uma preferência a estar perto do núcleo, mas noto que o elétron parece gostar mais de estar ou do lado de cima ou do lado de baixo, é quase impossível encontrar elétrons no anel lateral do átomo! Volte àquele desenho inicial e reflita sobre como ele é problemático. Os elétrons não giram em torno do átomo, a noção de trajetória nem existe, conseguimos apenas definir essas formas de probabilidade de medir o elétron em um lugar ou outro. Essa forma é a superfície na qual é igualmente provável encontrar um elétron. No caso das camadas 1s e 2s, essa superfície é uma esfera. A chance de encontrar um elétron afastado de uma distância $a$ do núcleo é a mesma para todos os lados, por isso dizemos que o orbital dessas camadas é uma esfera. No caso da 2p, vemos que essa forma muda, e ela será parecida com isso:
Com isso, em um abuso de linguagem, dizemos que o elétron “mora” nesses orbitais. A definição de orbital, contudo, não é o confinamento dos elétrons, mas as regiões equiprováveis de presença do elétron. Sabemos que a probabilidade de encontrar um elétron diminui exponencialmente quando nos afastamos do núcleo. ((Não estou usando exponencialmente como sinônimo de “grande” ou “bastante”, é literalmente exponencial!))
Quando você estava no cursinho, deve ter ouvido falar desses orbitais e das formas bonitinhas. Esse post é para tratar orbitais e elétrons de forma mais coerente com o que sabemos hoje em física, falando da incerteza da posição, a ausência da trajetória, as medidas de probabilidades, é isso o que sabemos sobre o elétron. Uma molécula envolve muitas vezes o compartilhamento de elétrons, e um orbital partilhado terá uma forma bem mais exótica que essas apresentadas pelo átomo de hidrogênio. Conforme você dá mais energia para o elétron, ele começa a poder ser encontrado mais longe do núcleo e, ao mesmo tempo, assume as formas mais estranhas de orbitais. Quando você vê um desses desenhos de orbitas, pense: a chance de eu encontrar um elétron é a mesma em todos os pontos dessa superfície.
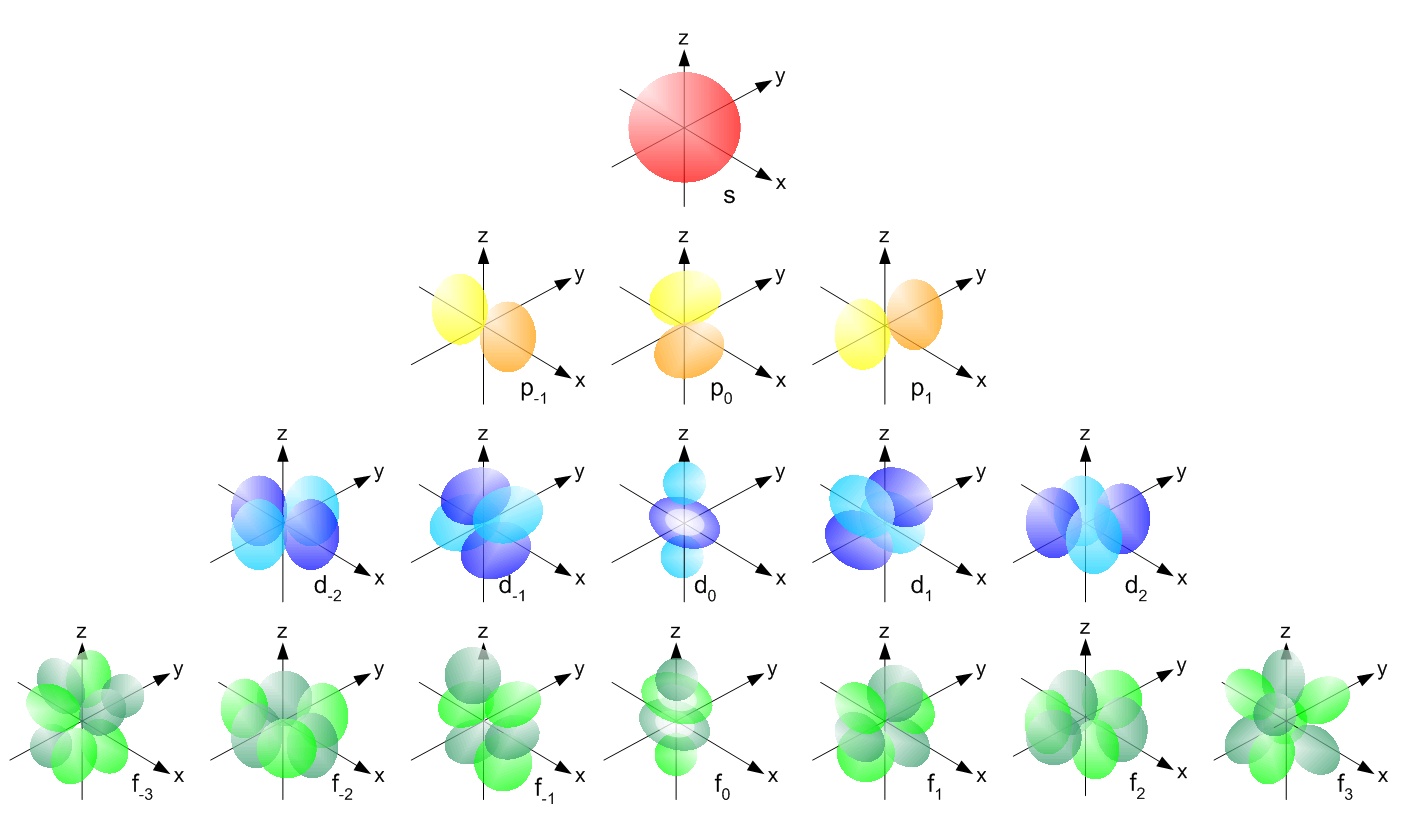
A origem dessas formas é a equação de Schrodinger, uma equação diferencial bem complicada que só pode ser resolvida exatamente para o caso de um elétron. Para mais elétrons, ou moléculas, ainda conseguimos resultados numéricos, ou seja, chicoteamos o computador até ele calcular essas formas com precisão para as moléculas que queremos. Mas fórmula exata, dessas bonitinhas que se cobra em prova, não temos, nem sabemos se existe.
Outra propriedade interessante dos orbitais, e dos elétrons em geral, é o princípio de exclusão. Tome, por exemplo, o orbital 2p, essas duas gotas. Se você tiver três elétrons em um átomo com a energia desse orbital, cada elétron ocupará um orbital em uma região diferente, serão ocupados os orbitais 2px, 2py e 2pz. Se você juntar outros três elétrons, cada elétrons entrará em um orbital e esse será o limite de ocupação. Você nunca consegue colocar mais que dois elétrons por orbital! Por mais que você tente calibrar seu elétron para entrar no orbital 2p, ele não será absorvido. A razão eu já mencionei uma vez quando disse o quanto me impressionava o princípio de Pauli, um dos resultados mais profundos e misteriosos da física.
Ao final do dia, o desenho tem um mérito. Ele representa camadas mais energéticas com círculos maiores, como se o elétron girasse com um raio maior. Isso não é verdade, ele não gira e não tem raio, nem trajetória tem, mas em camadas mais energéticas a chance de encontrar o elétron mais distante do núcleo é maior, como se ele tivesse mais “velocidade” e pudesse passear mais longe antes de ser puxado de volta para o núcleo.
E isso encerra o que queria te contar sobre o elétron, e espero que isso te guie um pouco por suas primeiras aulas de química, e te prepare para a desconstrução daquilo você você achava que sabe e que, como verá, ninguém parece saber.