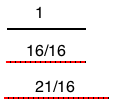Arquivos da categoria: Rookie

Posts para interessados em ciência.

A raiz do problema

Rookie

O teorema de Pitágoras é o centro da geometria de nossa oitava série, agora nono ano. Nele, aprendemos que há uma relação simples e até bonita entre os lados de um triângulo retângulo, aquele com um ângulo de 90°. O que não nos contam é a quantidade de problema que esse teorema já deu, e até as mortes que causou, na época de seu descobrimento. Os número irracionais já foram muito mais interessantes, quando havia gente que daria a vida, e mataria, para manter certas verdades ocultas na antiguidade clássica.

Pitágoras é uma figura historicamente bem misteriosa. Tudo o que se sabe sobre ele provém de séculos depois de sua morte, há mesmo quem duvide de sua existência, e todos os dados sobre ele são carregados de misticismo. Isso porque Pitágoras não era apenas um matemático, um professor, um sábio, ele foi além: em sua busca por conhecimentos e verdades nos números, enxergou um pouco mais do que devia e fundou um culto religioso envolvendo as verdades geométricas do universo.

Neste culto secreto, ciência e religião não possuíam diferença alguma e a busca pela verdade era também a busca pelo divino. O culto possuía regras de alimentação, comportamento, ser pitagórico era muito mais que pesquisar matemática, era um estilo de vida, e seu seguidores reuniam-se em uma mistura de escola com monastério no sul da atual Itália, no século V a.C.

Essa mistura não podia terminar muito bem. Diz-se na boca pequena, nesses boatos da história da matemática, que um infortunado descobriu que a raiz quadrada no número dois era um número irracional. Horrorizados com a notícia, os pitagóricos, e talvez até o próprio Pitágoras, mandaram matar este matemático para silenciar o que colocaria em cheque muito das verdades divinas descobertas pelo grupo. A razão do choque é difícil entender, mas vamos tentar, ela reside na ideia que os gregos tinham da natureza de um número.

Toda a matemática grega repousava na geometria, sua álgebra era fraca, a escrita era sempre feita em termos geométricos e os grandes trabalhos gregos versavam teoremas avançados sobre elipses, cônicas, parábolas, mas a ideia de equação está ausente em todos esses textos. Os números, como eles entendiam, eram sempre dados por proporções. Eles escolhiam um comprimento de linha, uma barra, para ser o 1. Mas isso não era “apenas” o número 1, a própria noção de número não existia muito, o 1 da contagem de ovelhas e o 1 da barra eram coisas diferentes para os pitagóricos, e gregos em geral. Essa barra de tamanho 1 representava a unidade, o fundamental, o que gera todas as coisas. E a definição de número dos gregos estava atrelada a isso. Dizer o número 3, a eles, era a barra cujo comprimento era três vezes o da barra unidade. Na ideia deles, dizer 3 era dizer:

Os demais números eram compostos de maneira parecida. A fração 21/16, por exemplo, não era ensinada com pedaços de bolo como em nossas quarta-séries, mas com pedaços da unidade. Você quebra a unidade em 16 pedaços, junta 21 deles, cola e tem o número que deseja:

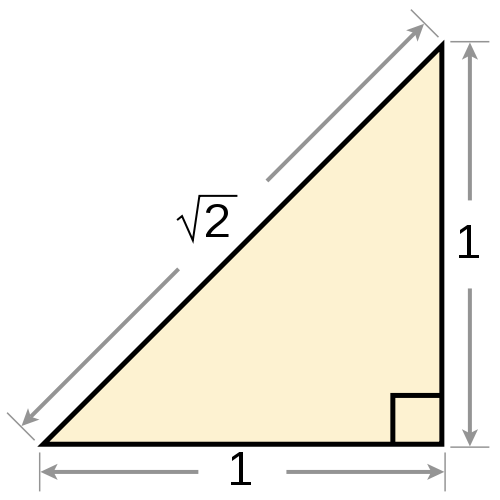
E assim eles faziam a matemática. Toda barra encontrada era “numerizada” quando se quebrava a unidade em partes pequenas o suficiente para, com um bom número delas, colar e formar a barra nova. E todo número novo era sempre pensado em forma de barra ou de pedaços de barra, toda a matemática eram intersecções, retas, circunferências e pontos. Até que, um dia, um homem, dizem Hipaso de Metaponto, descobriu uma barra que não era número. E, pior, ela estava o tempo todo bem embaixo do nariz de todos. Essa barra é a raiz quadrada de dois, uma barra tão facilmente obtida quanto alguém pode desenhar um quadrado:

Essa barra, a diagonal do quadrado, não pode ser composta com pequenos pedaços da lateral do quadrado, por menores que esses pedaços sejam. Isso não é nada evidente, você pode até tentar se enganar com a fração 141/100, mas ela ainda não é perfeitamente a diagonal do quadrado e nenhuma outra fração jamais será. Se antes eles apenas achavam que era uma barra cuja fração era complicada demais, isso é um abismo em relação à ideia de “não há fração para essa barra”. Em outras palavras, isso violava a própria noção de número dos gregos, algo alienígena à matemática deles, que estava profundamente atrelada ao religioso, à noção de proveniência da unidade, da formação do todo pelo pedaço primordial, ora, nada mais natural que silenciar o herege que descobriu esse pedaço de barra infiel.

A maneira como ele descobriu isso foi geométrica, mas posso dar um argumento algébrico legal de como nenhuma fração ao quadrado dá dois. Suponha que eu seja malandro, suponha que eu tenha encontrado dois números $p$ e $q$ tais que $\left(\frac{p}{q}\right)^2=2$. Como eu estou estudando a fração, é de bom tom que $p$ e $q$ não tenham divisores em comum pois, se tiverem, basta dividir a fração em cima e embaixo pelo número para ter uma fração equivalente (ou seja, 10/15 é o mesmo que 2/3, basta eu dividir os dois por 5).

Mas se $ \left(\frac{p}{q}\right)^2=2$, então $ \frac{p^2}{q^2} = 2$ e $ p^2 = 2q^2$. Até aqui sem surpresas, apenas apliquei o quadrado nos dois elementos e passei o de baixo multiplicando. No entanto, se $ p^2$ é duas vezes alguém, ele tem que ser par. Mas se $ p^2$ é par, então $ p$ é par, pois o quadrado de um número só é par se o próprio número for par, não tem como fazer um fator 2 “surgir” quando você multiplica um número por ele mesmo. Então $ p$ é par, e, como todo bom número par, é o dobro de alguém. Vamos chamar esse alguém de $ k$, então $ p=2k$. E se $ p^2 = 2q^2$, podemos substituir esse $ p$ por $ 2k$ e escrever $ (2k)^2=2q^2\implies 4k^2=2q^2\implies 2k^2=q^2$. De novo, sem surpresas, eu apliquei o quadrado nos dois caras da esquerda, percebi que podia dividir os dois lados da equação por dois e o fiz. Então eu provo que $ q^2$ é o dobro de alguém, o tal do $ k^2$, e, com isso, é par, o que faz o próprio $ q$ ser par também. Moral da história, se $ \frac{p^2}{q^2} = 2$, então tanto $ p$ quanto $ q$ são pares.

Contudo, eu havia suposto que $ p$ e $ q$ não possuíam divisores em comum! E acabo de provar que ambos são pares, então eles possuem um divisor em comum. Ora, posso dividir ambos por dois que a fração $ \frac{p}{q}$ ainda terá dois como quadrado, mas eu posso repetir o raciocínio acima e novamente provar que eles ainda são pares, então posso dividir de novo por dois e, aplicando o raciocínio acima, provar que ainda são pares! Ora, nenhum número é infinitamente par, está na cara que caímos em contradição nesse raciocínio e isso prova que nossa hipótese inicial é falha, pois ela nos conduz a um absurdo, que é um número infinitamente par. A verdadeira moral da história é: não existem números $ p$ e $ q$ tais que $ \frac{p^2}{q^2} = 2$.

E isso prova de maneira definitiva que a diagonal do quadrado é um alienígena no mundo da matemática grega, um número que não pode ser colocado como razão entre dois outros e, nessa medida, justamente chamado de irracional. A existência de tais números foi mantida em segredo por um bom tempo, poucos queriam seguir o exemplo de Hipaso. Hoje, não apenas sabemos que eles estão por toda parte, mas que a maior parte dos números reais é, de fato, de número irracionais. Em outras palavras, se você tirar um número real ao acaso, a chance é zero de tirar um que pode ser colocado em forma de fração, mas uma definição com mais cuidado disso tudo levaria a outro post, mas um indício pode ser encontrado em um outro, mais antigo, sobre os infinitos, onde vocês podem comprovar que, se as frações entram em uma fila, o raiz de dois, este incompreendido, não entra em fila nenhuma.

4 respostas

Poeira das estrelas

Rookie

Perguntaram em uma entrevista ao grande astrofísico Neil deGrasse Tyson qual ele julgava o fato mais fascinante da ciência. Como bom físico, ele podia escolher de uma vasta gama de coisas impressionantes sobre a natureza e o universo, e decidiu pela grande jóia da astrofísica: a nucleossíntese dos átomos pesados. Esse nome parece impressionante e difícil, mas não conheço nenhum outro fato que seja tão impressionante, belo, poético e impactante quanto descobrir de onde vieram os elementos que compõem cada um de nós e o que nos cerca.

Em termos apenas científicos, não seria desonesto responder ao “de onde viemos” com a palavra “Big Bang”. Isso é verdade, mas é também uma resposta incompleta, o Big Bang produziu, no máximo, átomos de hidrogênio para todo o lado, e somos compostos de muito mais do que isso. A formação dos átomos de hidrogênio no Big Bang é um assunto também fascinante, a maneira como as reações químicas competem com a expansão do universo nesse período primordial é para ser assistida com pipoca, mas fica para outro post. Vamos entender como chegamos dos átomos de hidrogênio, o número 1, aos de urânio, número 92, passando por todos os que conhecemos da tabela periódica (exceto o tecnécio, número 43, que é instável, e isso é outro fato legal sobre a ciência).

Tudo começa há muito tempo atrás, em uma galáxia muito, muito distante, o hidrogênio que por lá havia se concentrou mais do que devia. Gases andam de um lado para o outro no universo, eles se atraem por força gravitacional e se dispersam pelo fenômeno normal de dispersão, como o cheiro de um perfume se dispersa em uma sala quando aberto o frasco. Mas se a concentração é forte o suficiente, sua gravidade vence essa dispersão e ele começa a se acumular, inicia o processo de formação de uma estrela.

O destino dessa estrela dependerá da quantidade de hidrogênio inicial, a menos de patologias (caso ela absorva mais gente, enfim, o espaço é uma selva, muita coisa pode acontecer). Vou descrever o processo de uma estrela bem massiva. O Sol não se enquadra nesse processo, ele irá parar em algum estágio intermediário para seguir algum outro destino, o que descrevo é a sina das estrelas massivas.

Aquele hidrogênio todo começa a se acumular, e o centro dele começa a ganhar pressão, um processo parecido a você apertar uma seringa cheia de ar e perceber que o que há dentro dela atinge uma tal pressão que você não consegue mais apertar. Com a estrela, esse aumento de pressão vem com aumento de temperatura, porque em matéria de volume ela não tem tanta escolha. Isso é resultado daquele $PV = nRT$ do seu colégio, com $P$ alto, $T$ tem que também ser alto. Em termos microscópicos, as partículas do interior da estrela tomam porrada (pressão gravitacional) de todas as que estão fora, elas acabam ganhando velocidade (temperatura) e dão porrada de volta, nada mais justo.

O problema é que a estrela brilha (na verdade, tudo brilha, eu e você brilhamos, mas isso fica para outro post), e esse brilho a faz perder energia. Em termos microscópicos, o hidrogênio em torno dela consegue ir mais perto do centro em algum momento (o que seria uma “queda” do hidrogênio, ele ganha velocidade), ele brilha, manda luz e perde velocidade, então não consegue voltar para a altura que estava. Toda a estrela, nesse processo, fica mais junta, e a pressão gravitacional no centro aumenta, aquele hidrogênio tem que ficar ainda mais quente para segurar todo o entorno da estrela que está mais próximo e batendo com mais vontade.

Temperatura é a velocidade média das partículas. Aquele hidrogênio do centro está tão rápido que, em uma manobra bem colocada, colide de frente com outro hidrogênio e eles formam hélio. Mas não é uma reação amigável, o choque causa uma liberação de energia muito grande. Em outras palavras, o hélio, quando se forma, está em alta velocidade de vibração e bate nos outros hidrogênios, aumentando a temperatura do local e segurando a pressão do resto da estrela. Esse processo acontece com diversos átomos de hidrogênio e logo o centro da estrela é composto de hélio, envolto em uma estrela toda de hidrogênio.

O hélio deve esquentar cada vez mais, para segurar aquela pressão sempre aumentando, pelo mesmo problema de antes. Em um momento, a temperatura do hélio é tão alta que ele pega outro de jeito e forma berílio, que rapidamente vai encontrar outro hélio e formar carbono. O berílio não aparece muito porque ele facilmente vira carbono, mas o carbono dificilmente vira outra coisa. Teremos, com isso, um núcleo de carbono envolto em uma camada de hélio rodeada de hidrogênio, nossa estrela será uma cebola de elementos, com o centro mais pesado que as bordas.

E assim continuaremos, com um centro sempre aquecendo e novos elementos colidindo e se formando. Esse ciclo continua até a formação do ferro (na verdade, acho que vai até o níquel, mas ele rapidamente vira ferro) e teremos uma estrela gigantesca em diversas camadas de elementos como uma cebola, cuja figura fica mais ou menos assim:

Mas se enganam os que acham que nossa fábrica de átomos continuará esse processo até o urânio. A partir do ferro, a fusão de dois elementos não libera mais energia; não há aquela história de colidir dois e aumentar a velocidade. Aos que se lembram da química, dizemos que a partir do ferro a reação de fusão torna-se endotérmica. Com isso, a estrela para por aí, com um grande e crescente núcleo de ferro.

Mas não somente há outros elementos na natureza como você é feito de alguns deles (o zinco e o iodo, por exemplo). Podemos, contudo, já perceber que esse mecanismo explica a grande abundância de elementos mais leves que o ferro na natureza, inclusive a abundância de ferro, e a raridade dos mais pesados, como o ouro, a prata e a platina. O sistema de produção dos elementos mais pesados era um mistério, até proporem que esses elementos são formados na morte das estrelas.

Esse processo não continuaria infinitamente. A temperatura no núcleo de ferro chegaria a valores tão altos que algumas reações impensáveis na nossa realidade começariam a acontecer, uma delas é a união de elétrons com prótons para formar nêutrons. Não é muito famoso o fato de nêutrons não serem caras que, sozinhos, são estáveis, eles levam em média 15 minutos para virarem um próton e um elétron. Mas se a temperatura está muito alta, o processo inverso pode acontecer, e acontece. O problema é que quem segurava a pressão da estrela toda eram os elétrons, eles sumindo, o núcleo colapsa: todo aquele núcleo de ferro é completamente vencido por sua gravidade e se comprime em uma densidade tão impressionante que você conseguiria enfiar uma caminhote em um dedal, ou o Sol em uma bola de 10Km. A única coisa que impede o núcleo de se contrair ainda mais com sua gravidade é a força forte, em outras palavras, a densidade dessa massa é a mesma da densidade do núcleo de um átomo: a maior que é possível atingir.

Então temos isso: um núcleo comprimido ao extremo pela força gravitacional que vai puxar todo o resto da estrela para si. Esse resto, as outras camadas da cebola, será puxado com extrema violência e, assim que a primeira camada colide com o centro, ela é rebatida com praticamente a mesma velocidade, porque o núcleo não pode se comprimir mais e a única opção é ricochetear o que o atinge. Mas essa primeira camada agora está voltando enquanto todas as outras estão vindo, elas irão se colidir possuindo tanto massa quanto velocidades fora de qualquer coisa que possamos imaginar. Tais choques serão tão fortes que poderemos formar todos os demais elementos da tabela periódica depois do ferro, todos resultantes da explosão de uma estrela que, nesse momento, está se tornando uma estrela de nêutrons (apenas aquele núcleo super denso vai sobrar, o resto explodiu e foi embora), essa explosão é conhecida como supernova.

Esse processo todo não é rápido. A estrela passa a maior parte do tempo “queimando” hidrogênio para fabricar hélio, menos tempo passando do hélio para o carbono e assim por diante, o tempo gasto em cada processo depende do tamanho dos átomos, sendo o que leva aos átomos mais pesados mais rápido. E também vale lembrar que o que descrevi é apenas um destino possível da estrela, a maneira como cada uma pode morrer é bem variada, depende da massa e de quem está na vizinhança.

A explosão de uma supernova libera muita matéria e, sendo ela dificilmente isolada, acaba se tornando ingrediente para a formação de novas estrelas. Não por menos, há regiões do espaço conhecidas como “berçário de estrelas”, locais de grande acúmulo de matéria onde a densidade limite é atingida com frequência e estrelas aparecem.

Se essa explosão acontece próxima à Terra, podemos ver com clareza o aparecimento de uma estrela muito brilhante durante três meses. Diversos povos na antiguidade relataram essas estrelas, sua luminosidade era tão intensa que uma noite de lua nova ainda era visível pela luz que essa explosão emitia. A última supernova próxima a Terra foi em 1986, e esses eventos são raros, é difícil haver mais que uma próxima a cada 400 anos.

No entanto, todos os elementos pesados que conhecemos, o ouro, a prata, a platina, o chumbo, o zinco do seu corpo, o cobre, o tungstênio que compõe o filamento de sua lâmpada, o mercúrio do termômetro, o iodo do seu sal, todos eles se formaram da explosão de uma estrela. Os mais leves que o ferro se formaram enquanto ela morria e são apenas liberados nessa explosão. Nisso, as estrelas são fábricas de átomos pesados, o que permite nosso universo de ser composto de mais que hidrogênio, e o que permite nossa existência, compostos desses átomos variados, uma intrincada rede de reações eletroquímicas e, em última análise, poeira das estrelas.

3 respostas

Cabras, Ferraris e probabilidades

Rookie

Ricardo: Hoje contaremos com um post de um convidado especial, e mais entendido que eu no assunto. Pedro Natal é um gaúcho iteano que atravessou comigo a Polytechnique e seguiu para ser mestre em matemática aplicada pela Universidade de Paris. Tem por vícios chá inglês, café forte e propor problemas matemáticos à turma quando nos reunimos em algum KFC. Sem mais, entrego-lhes uma leve discussão sobre cabras e probabilidades.

Embora o título logo acima possa levar a crer que discorreremos sobre uma peça de teatro do absurdo, o assunto principal deste texto é matemática. Mais especificamente: cabras, Ferraris e programas de auditório; não precisamos de mais que um conhecimento básico desses três itens para seguirmos. E, convenhamos, o que há de melhor para aguçar nossos sentidos probabilísticos do que histórias envolvendo Sílvio Santos, ruminantes e carros de corrida?

Suponha que você esteja num programa de auditório estilo Sílvio Santos, e que você deva escolher uma dentre três portas. Uma delas esconde uma Ferrari; as outras duas, simples cabras. Você escolhe, digamos, a de número 1. Nesse momento, antes de revelar o resultado da sua escolha, Sívio Santos $-$ que sabe onde está a Ferrari $-$ abre uma das outras duas portas e revela uma cabra. Ele então pergunta: “Você muda a sua escolha ou continua com a número 1?”. Em outras palavras, existe alguma vantagem em trocar de porta?

Se essa é a primeira vez que você se depara com esse problema, eu sugiro honestamente que você aproveite para pensar nele antes de ler o próximo parágrafo. A resposta correta é mais interessante do que parece e está longe de ser trivial.

É possível que você tenha chegado à seguinte conclusão: como só restam duas portas, cada uma delas tem 1/2 de chance de conter a Ferrari, e logo não há vantagem em trocar de porta. Infelizmente, esse raciocínio não está correto. Sim, existe uma vantagem em trocar de porta. A probabilidade que a porta inicial contenha a Ferrari é 1/3, ou seja, a probabilidade de ganhar trocando de porta é de 2/3. Por quê? A maneira mais fácil de entendê-lo é com o seguinte desenho (que eu não tive vergonha de roubar da Wikipédia):

A figura da esquerda mostra que a probabilidade de você ter acertado na sua primeira escolha é de 1/3, ou seja, a probabilidade que a Ferrari esteja em uma das outras duas portas é de 2/3. Quando Sílvio revela a cabra, ele não altera as probabilidades calculadas anteriormente! Assim, como vemos na figura da direita, a probabilidade de encontrar a Ferrari trocando de porta é de 2/3.

Esse famosíssimo problema, conhecido como Problema de Monty Hall, gerou muita confusão e discussão nos EUA há pouco mais de 20 anos. Ele foi publicado por uma colunista chamada Marylin vos Savant na revista Parade em 1990, e desencadeou uma enxurrada de respostas furiosas da parte dos leitores que não aceitavam que a resposta fosse diferente de 1/2 (reza a lenda que, das 10 mil reclamações recebidas, mais de mil foram redigidas por pessoas com um PhD).

Mas o que há de errado afinal com o raciocínio que leva à conclusão de que não há vantagem em trocar de porta? Um pequeno detalhe: Sílvio Santos sabe o que há atrás das portas. O raciocínio seria correto se a porta a ser revelada fosse escolhida ao acaso, mas ela não é! Sílvio Santos nunca vai revelar a Ferrari para o jogador, e é essa assimetria que gera a assimetria probabilística do problema,

Como observado pelo (meu grande amigo) dono do blog Todas as configurações possíveis, existe ainda uma outra maneira intuitiva de se compreender a vantagem em mudar de escolha: se houvesse 1000 portas, você escolhesse uma, e Sílvio abrisse 998, revelando cabras em todas elas, você trocaria? Qual é, honestamente, a chance de você ter acertado de primeira?

Ao leitor que não ficou convencido com esses argumentos intuitivos: uma prova mais formal (mas menos astuciosa) envolvendo a famigerada fórmula de probabilidade condicional existe. Não por acaso, é exatamente o conceito de probabilidade condicional que está por trás da confusão que o Problema de Monty Hall gera na nossa intuição.

As histórias divertidas envolvendo probabilidade não acabam por aí. Num futuro artigo, que deve ser matematicamente (um pouquinho) mais complicado, falaremos sobre as peculiaridades da mistura de álcool, probabilidades condicionais, e cadeias de Markov!

Deixe um comentário

Prova surpresa

Geek Hardcore Rookie

O post de hoje não é muito informativo, é mais perturbador, um probleminha de lógica para não deixar você dormir.

Um professor chega à aula e avisa sua classe que aplicará, no mês de abril, uma prova surpresa. Um aluno, que futuramente se tornaria matemático na área de lógica, pergunta o que o professor entende por surpresa. Estranhando a pergunta, o professor responde que uma prova surpresa é uma prova tal que, no início de cada dia do mês de abril, os alunos não podem deduzir ou saber que a prova será aplicada naquele dia. Triunfante, o aluno conclui que não haverá prova nenhuma, pois:

– Se a prova não for aplicada até o 30 de abril, então ela terá que necessariamente ser nesse dia e, no começo do dia, já não será surpresa. Então o 30 de abril não pode ser a data da prova.

– Se a prova não for aplicada até o 29 de abril, então ela terá que ser necessariamente nesse dia, pois o 30 está excluído. Mas, assim sendo, ela não será uma surpresa, então o dia 29 não pode ser o dia da prova.

– Se a prova não for aplicada até o 28 de abril, então ela terá que ser necessariamente nesse dia, pois o 30 e o 29 estão excluídos. Mas, assim sendo, ela não será uma surpresa, então o dia 28 não pode ser o dia da prova. E assim por diante, ele exclui todos os dias.

No dia 12, ele recebe a prova. Onde ele errou?

7 respostas

O segundo bissexto

Rookie

Os que nascem hoje envelhecem menos que os outros. Comemorando apenas aniversário uma vez a cada quatro anos, os nascidos no vinte e nove de fevereiro são agraciados com problemas em preencher formulários online o resto de suas vidas, mas são privilegiados, nasceram em um dia especial, resultado de a rotação da terra em torno do Sol possuir alguns quebrados depois do 365 dias.

Esses quebrados são corrigidos com esse dia, mas até os quebrados possuem quebrados e esse ajuste não é perfeito. Precisamos pular um ano bissexto a cada 100 anos, e o fazemos, mas nem esse ajuste é ideal; podemos pular apenas os anos bissextos múltiplos de 100 que não são múltiplos de 400 (o que explica o ano 2000 ter sido um bissexto tão especial, a exceção da exceção). Isso deixa as coisas mais acertadas, só começaremos a perceber os efeitos dos quebrados dos quebrados em muitos milênios.

Enquanto o 29 de fevereiro é bem famoso, seu equivalente menor, o segundo bissexto, ou segundo adicional, não é muito conhecido. Diversos anos no último século contaram com o segundo adicional, suas contagens de ano novo estavam quase sempre adiantadas. Os grandes relógios atômicos do mundo que regem a contagem padrão das horas na terra estão cientes desse fato, há um conselho que define quando um ano terá um segundo extra e, quando isso acontece, o relógio do dia 31 de dezembro ou 30 de junho mostra, durante um segundo, a marca 23:59:60 antes de ir ao 00:00:00. Se não acredita, veja este relógio atômico:

[youtube=http://www.youtube.com/watch?v=34wDgYEOUJU]

Enquanto é fácil entender o 29/02, ele resulta do fato de a rotação da Terra em torno do seu próprio eixo e sua rotação em torno do Sol não serem múltiplos perfeitos, o segundo bissexto é mais difícil. Nós definimos o segundo como bem entendemos, não poderíamos ter definido um segundo que coincide exatamente com um divisor inteiro do dia terrestre, e não precisar acrescentar segundos, já que o ano possuiria um número exato de segundos, sem quebrados? Poderíamos, e fizemos isso, no século XIX. Mas o dia, desde então, se tornou mais longo. Vamos entender a razão disso.

Você deve ter visto a Lua diversas vezes à noite. Quando eu era menor, eu e minha mãe conversávamos sobre o que víamos “desenhado” na Lua. Ela via um coelho, há quem veja São Jorge e um dragão, eu via um rosto triste. E em todas essas conversas, eu jamais havia reparado: eu via sempre a mesma coisa na Lua. Mas se a Terra gira, em torno de si e do Sol, como a Lua conspira para sempre ter a mesma face virada para nós?

The Dark Side of the Moon não é apenas um excelente album do Pink Floyd, é como é chamado o lado oculto da Lua. O nome engana, esse lado da Lua recebe a mesma quantidade de luz solar que o outro lado, mas nunca o vemos da Terra. O período de rotação da Lua em torno de si mesma é exatamente o mesmo de sua rotação em torno da Terra, por isso ela sempre aparece com o mesmo rosto em nossas noites. Isso acontece pelas chamadas forças de maré, a força gravitacional da Terra afeta a Lua de tal forma que, por mandar gases e líquidos de um lado para o outro, a rotação da Lua acabou desacelerando e atingindo uma configuração estável. Se a Lua está sempre com o mesmo lado virado para a Terra, não há mudanças entre “maré alta” e “maré baixa” nela, então a rotação não perde mais velocidade. Se perdesse mais, essa variação recomeçaria, essa configuração de “lado oculto” e “lado visível” é a mais estável que a Lua consegue encontrar.

Longe dos filmes B de ficção científica, a rotação da Terra está, aos poucos, perdendo velocidade pelo mesmo motivo da Lua: o Sol causa suas forças de maré e pouco a pouco nossa rotação diurna vai se ajustando à rotação anual. Em muitos bilhões de anos, a Terra terá essas rotações coincidentes, teremos um lado constantemente exposto ao Sol e outro oculto, dia perpétuo e noite perpétua.

A Lua gira em torno da Terra há menos tempo (ou ao menos o mesmo tempo) que a Terra gira em torno do Sol, mas esse “acoplamento de maré” aconteceu muito antes na Lua que na Terra porque a distância Terra-Lua é bem menor que a Terra-Sol e o tamanho da Lua é bem menor, as forças de maré surtem mais efeito nela. No século XIX, os físicos definiram o segundo. Agora, para compensar o ganho de 2 milissegundos (0,002 segundos) de nosso dia por século (sendo cada ano 365 dias, se cada um deles fica 2ms mais longo, isso equivale a um ano 0,73s mais longo), inserimos o segundo bissexto. O último ocorreu no Reveillon de 2008 e o próximo será dia 30 de junho deste ano.

Enquanto isso pode não parecer muito, é interessante notar que os dinossauros, tendo vivido há 180 milhões de anos, possuíam dias uma hora mais curtos, a rotação da Terra era mais rápida. Em muitos milhões de anos, teremos dias cada vez mais longos, nossos descendentes, se existirem, poderão dormir 12 horas e ainda trabalhar outras 16. Eu, decididamente, nasci na época errada.

1 resposta