Arquivos da categoria: Rookie

Posts para interessados em ciência.

Aniversários

Rookie

Hoje é meu aniversário, celebro vinte e quatro anos de vida. E essa data, além de me fazer sentir especial, costuma me lembrar de um problema fascinante de combinatória, que levou a um igualmente interessante estudo econômico. Como não achei referência ao estudo, nem lembro onde o li, repeti-o eu mesmo, na medida do possível. O problema é conhecido como paradoxo do aniversário, que de paradoxal não tem nada.

A pergunta é: quantas pessoas eu preciso colocar em uma sala para que a chance de haver naquela sala pessoas com o aniversário repetido seja maior que a chance de não haver pessoas com o aniversário repetido? Formulado de outra maneira, eu tenho $N$ pessoas em uma sala e uma probabilidade $P(N)$ de que essas pessoas possuam aniversário repetidos, qual o primeiro valor de $N$ para o qual $P(N)>0,5$?

E a resposta é um número surpreendentemente baixo: 23. A partir desse valor de pessoas, é mais provável encontrar pessoas com aniversários repetidos que não encontrar, a probabilidade de que duas pessoas tenham nascido no mesmo dia do ano passa a 50,7% para esse valor de $N$. A razão do número ser pequeno é o grande crescimento da função fatorial, usada para calcular o número de combinações possíveis para a comparação de cada par de pessoas. Ou seja, apesar de haver muitos dias no ano, o número de comparações possíveis entre o aniversário de 23 pessoas é suficientemente grande para tornar essa probabilidade maior que 50%.

Interessados nesse resultado, podemos testar os aniversários de partidas de futebol. Sendo 11 para cada lado e o juiz, teremos 23 pessoas a cada partida, e podemos comparar um número grande de partidas para perceber que há mais partidas com aniversários repetidos que partidas sem aniversários repetidos.

No entanto, o resultado não será o que esperamos. De fato, há muitas partidas com aniversários repetidos, mas um número muito maior que o esperado! As partidas com aniversários repetidos ocorrem em número muito maior que as que não possuem aniversários em comum, quando a diferença não deveria estar muito longe de 51% contra 49%. Esse fato foi-me apresentado há algum tempo, foi-me até dito que um estudo foi feito, jamais achei o estudo, fi-lo eu mesmo com a ajuda da Wikipédia e sua excelente página da escalação de cada seleção de futebol.

Pus-me a anotar os meses de nascimento dos jogadores de futebol das seguintes seleções: Brasil, Paraguai, Chile e Argentina. Tomei a escalação mais atual possível, para não haver privilégio de uma época ou outra. A razão de pegar apenas países do hemisfério sul ficará clara com os resultados.

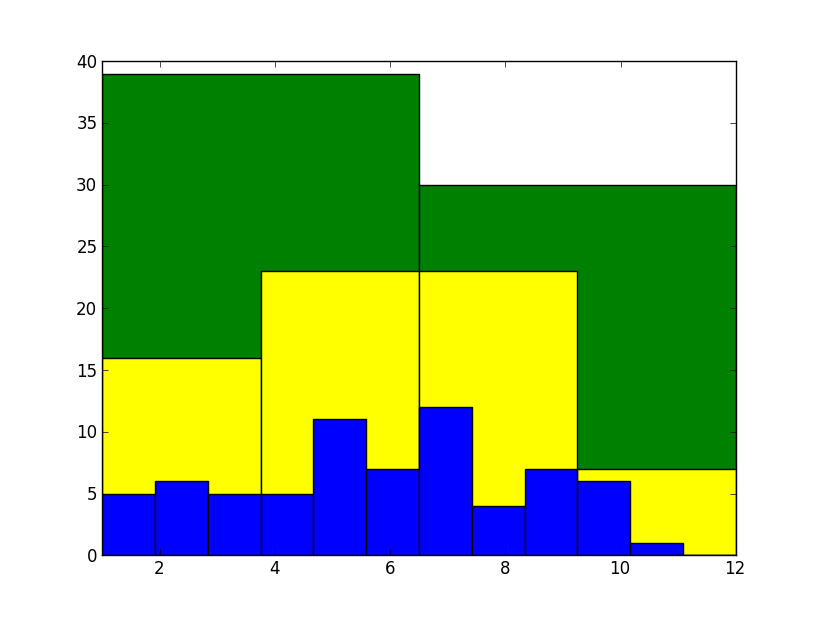
Enquanto o Paraguai não apresenta uma distribuição de nascimento de seus jogadores ao decorrer do ano que chame a atenção, Brasil, Chile e Argentina impressionaram-me e comprovaram, em termos nada rigorosos, a teoria que eu havia ouvido a respeito do estudo. Organizei um histograma em três camadas, as barras menores são os nascimentos no mês, as intermediárias representam nascimentos em um trimestre e as grandes são os nascimentos no semestre. O resultado do Paraguai, analisados 83 jogares, foi:

Nada impressionante até aqui, os aniversários parecem razoavelmente bem distribuídos em todos os níveis e não consigo perceber uma tendência evidente. No entanto, a distribuição do Brasil já começa a apresentar um fenômeno interessante:

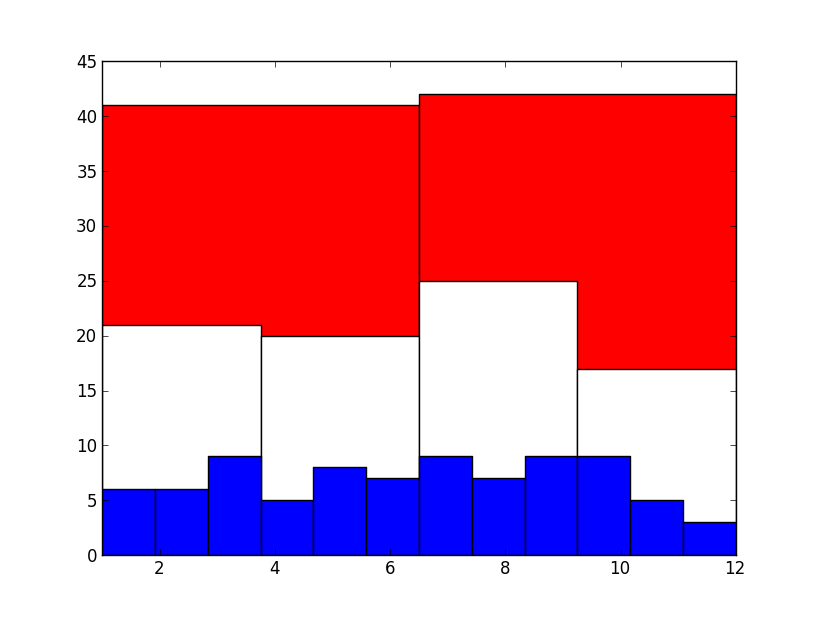
Temos na seleção brasileira, analisados os 69 últimos convocados de Mano Menezes, uma concentração clara de nascimentos no primeiro semestre, em especial uma forte ausência de nascidos no último trimestre do ano. Claro, isso pode ser uma improbabilidade realizada, não um indício de variável escondida. Se analisarmos com cuidado, podemos calcular a probabilidade de, jogando aniversários aleatoriamente no ano, ter essa diferença entre o primeiro e o segundo semestre; é improvável, mas nem de longe impossível.

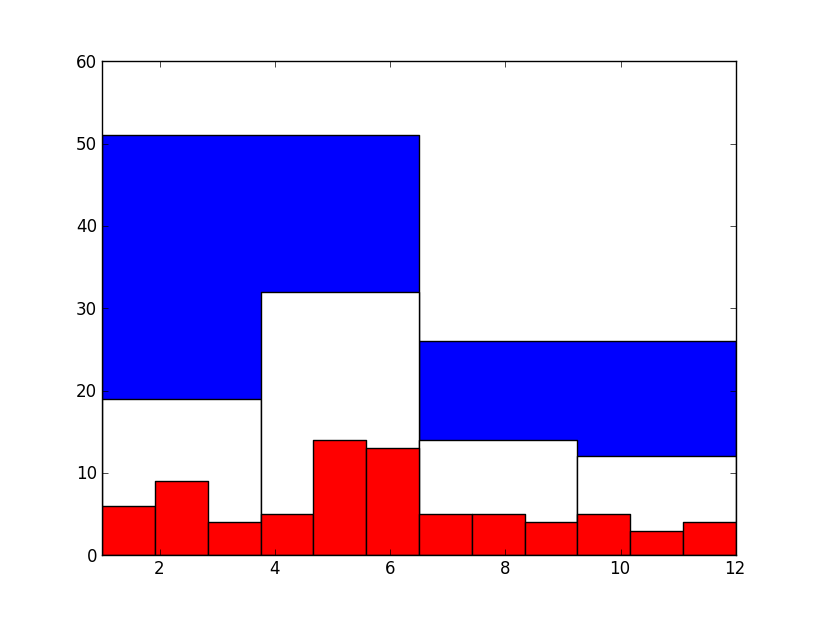
No entanto, os resultados do Chile, analisados 77 jogadores, revelaram-se:

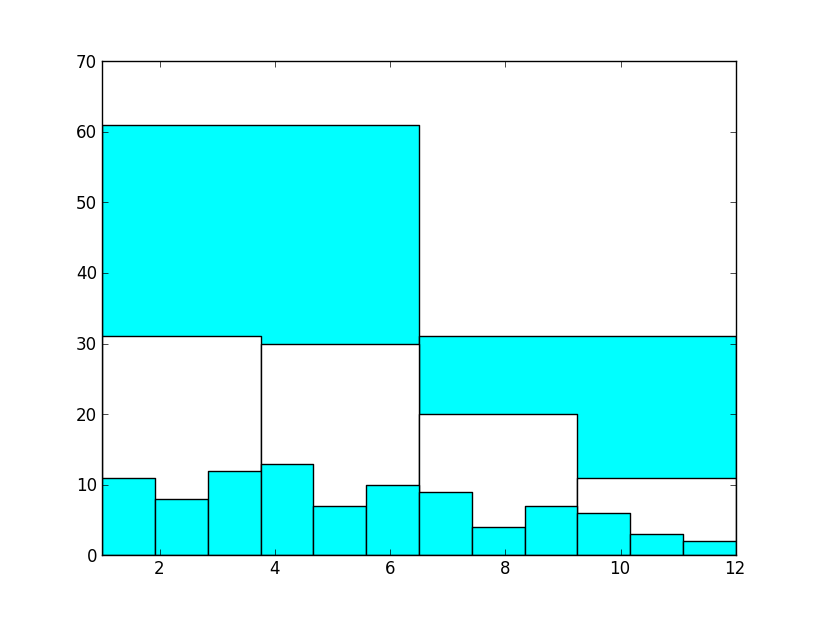
E essa diferença entre primeiro e segundo semestre já não pode mais ser explicada como uma anomalia estatística, há algo estranho nesse país que faz jogadores de futebol nascerem no começo do ano e não no final. Para confirmar a teoria, podemos avançar no estudo da seleção Argentina, analisando 92 jogadores:

Esse gráfico não pode, de maneira alguma, ser justificado como coincidência. A albiceleste possui o dobro de jogadores nascidos no primeiro semestre em relação ao segundo semestre. Entrementes, notamos que em todas as seleções dezembro é sistematicamente o pior mês, ou o segundo pior, no caso do Chile.

Podemos nos divertir calculando a probabilidade de obter uma configuração como a da Argentina se os aniversários fossem distribuídos de maneira uniforme no ano. Temos 92 jogadores e queremos saber a chance de, distribuindo aleatoriamente no ano, ter uma diferença de 30 nascimentos entre os dois semestres, sendo o primeiro semestre o favorecido. Calculando com cuidado, essa probabilidade não passa do valor 0,08%, extremamente baixa, ela precisa de uma explicação.

Antes que os astrólogos saiam em defesa de alguma correlação entre estrelas e seres humanos, comento a conclusão a que chegaram os estatísticos. Essa predominância de nascimentos em um semestre não ocorre em países europeus, curiosamente, analisei França e Inglaterra e os resultados não são nada impressionantes. Esses três países do sul, Brasil, Argentina e Chile, apresentam sistematicamente jogadores nascidos em um semestre, e a razão disso, muito provavelmente, é o ano letivo.

No mesmo argumento que usou Malcolm Gladwell em seu livro Outliers para explicar jogadores de hóquei, nesses países, as escolas de futebol organizam os alunos de acordo com o ano letivo, e os jogadores profissionais enfrentam peneiras desde cedo para seguir na carreira. Os nascidos no começo do ano são, por isso, os mais velhos de suas turmas e, ao enfrentam peneiras desde crianças, são também os mais fortes e mais rápidos. Os nascidos no primeiro trimestre são quase um ano mais velhos que os nascidos no último, e são selecionados em uma idade em que um ano é muito para o desenvolvimento corporal. Esse resultado é ausente nos times europeus porque as escolas de futebol não seguem um ano específico, algumas tomam o escolar como base e outras o ano de nascimento, não havendo consenso, há equilíbrio na distribuição.

Falta, claro, explicar o caso do Paraguai. Tendo em vista os outros países, o mais natural é supor, ou que o Paraguai é a anomalia estatística, ou que o sistema de escola de futebol e peneira desde muito cedo não é tão rigoroso no Paraguai.

Tudo o que eu acabo de fazer, aviso, consiste em estatística de péssima qualidade. Eu precisaria tomar vergonha na cara, analisar mais jogadores de mais times, informar-me sobre o sistema de avaliação do Paraguai e não me ater a essa tese com muito afinco, ela pode muito bem estar furada. Contudo, os 0,08% chamam a atenção, e confirmam que o estudo do paradoxo do aniversário não pode ser realizado com jogadores de futebol.

Claro que a hipótese feita, a distribuição igual de nascimentos ao redor do ano pela população normal, precisa ser justificada. Redireciono-os ao trabalho desse site, enquanto aponto ao curioso fato do grande número de nascimentos em setembro-agosto, provavelmente resultado das férias de natal, quando a chance de se estar em casa é alta e a programação da televisão cai de qualidade vertiginosamente.

Se o futebol sul-americano já apresenta esse fenômeno, podemos encontrá-lo de forma ainda mais acentuada em esportes cuja dependência da disposição física (e, logo, da idade) seja maior, o hóquei é um bom exemplo. Um grande estudo nesse aspecto foi realizado no Canadá em 1988 e os resultados do estudo são impressionantes, o mês de nascimento parece ter implicação direta no sucesso do jogador. Atualmente, parece que as ligas americanas e canadenses adaptaram um calendário diferente, mais próximo daquele europeu de futebol, e a diferença não é mais gritante.

E esses gráficos nos inspiram a questionar o quanto do sucesso de alguém em uma carreira é fruto de sucesso inicial, de ter se dado bem no começo, gostado, continuado, se esforçado e se dado ainda melhor, um círculo vicioso positivo vindo apenas do fato de ter sido bem sucedido no começo. Extrapolando, podemos nos perguntar se fazemos o que fazemos pelo sucesso inicial, e me pergunto quanto da matemática que faço não vem de uma primeira nota alta na matéria. As coisas talvez tivessem sido diferentes se eu tivesse errado mais questões, se minha professora fosse uma carrasca, se a ponta de meu lápis tivesse quebrado naquela primeira prova ou, quem sabe, se eu tivesse nascido em junho.

19 respostas

A pior forma de governo

Rookie

As eleições na França tiveram há pouco sua conclusão, com a vitória do socialista François Hollande, e logo as eleições americanas começarão. Eu conversava com um amigo francês a respeito, ele, em um não raro surto nacionalista, dizia ser raro encontrar um país com uma democracia tão funcional quanto a francesa, em que candidatos em igualdade de condições (mesmo tempo de propaganda eleitoral, por exemplo) são avaliados de forma justa e o escolhido é o favorito da população. Comparava esse sistema ao confuso método americano de eleições indiretas, que pode gerar aberrações estatísticas como a estranha eleição de Bush sem a maioria absoluta da população. Ainda, argumentei que o escrutínio francês não é perfeito, o método de eleição em dois turnos não é ideal. Ele perguntou qual seria, então; e a resposta é simples, e longe de intuitiva: nenhum método é justo.

Se Churchill disse que a democracia é a pior forma de governo, exceto todas as outras que já foram tentadas, o post de hoje é para convencê-los de que até em um caso bem simples a democracia não possui resposta fácil, a justiça nem sempre é evidente e uma eleição possui fatores que vão além de músicas contagiantes, propagandas elaboradas e discursos violentos.

Somos confrontados diversas vezes com situações em que uma eleição deve ser realizada, não damos a devida atenção ao método do escrutínio. Digo que não apenas ele amplifica ou ajuda um resultado, muitas vezes a forma de escrutínio determina o vencedor. Para não forçar meu argumento, vou listar os métodos mais tradicionais de escrutínio, todos baseados em sistemas existentes:

1º Método: eleições em um único turno. Inspirados em sistemas de democracia pequena, como a eleição para “chefe do grupo” ou para o diretório de estudantes de uma universidade, podemos apenas contar, em uma votação com uma opção apenas, quem tem mais votos e decidir que ele será o escolhido.

2º Método: eleições em dois turnos. Inspirados nas eleições francesas e brasileiras, podemos realizar uma primeira votação e, selecionados os dois melhores, podemos realizar um segundo turno e eleger vencedor o que obtiver então mais votos.

3º Método: atribuição de pontos. Inspirados nas eleições legislativas australianas, podemos atribuir pontos a suas preferências: 5 pontos ao favorito, 3 ao segundo favorito, 1 ao terceiro lugar e 0 ao que não querem de jeito nenhum. O candidato que ganhar mais pontos é eleito.

4º Método: contagem de confrontos. Inspirados nas eleições americanas, com um sistema um pouco diferente, podemos pensar em um sistema de “confronto” entre candidatos. Quantas vezes o A é preferido em relação ao B? E ao C? E ao D? Após todas essas comparações, ou confrontos, somamos o “placar” de cada candidato e o que tiver vencido mais confrontos é o eleito. Em outras palavras, é como simular todos os “segundos turnos” possíveis e eleger o candidato que vencer mais segundos turnos.

Todos esses métodos são usados em algum sistema democrático de comparação na vida real, não inventei nada. Ainda, digo a vocês que é impossível estabelecer um vencedor único, aliás, consigo situações em que é impossível encontrar um vencedor “justo” da eleição. Se você considera esses quatro métodos válidos, sigo contando a história de um país bem pequeno.

Apresento a vocês Pequenolândia, um país de dez habitantes que quer eleger seu presidente (não confundir com Pequenópolis, oficialmente cidade natal de Clark Kent). Quatro candidatos se apresentam, A, B, C e D. Cada cidadão possui para si uma ordem de prioridade na escolha dos candidatos, e eu apresento essa ordem em forma de tabela:

Eleitor 1 2 3 4 5 6 7 8 9 10
1º A A A A B B B C C D
2º D C D D C C C D D C
3º B D B B D D D B B B
4º C B C C A A A A A A

A constituição de Pequenolândia, contudo, não está escrita, eles precisam de um presidente para isso. Sem saber como realizar as votações, os habitantes de Pequenolândia se inspiram nas diferentes formas de classificação eleitoral pelo mundo, e, decididos a exercerem plenamente a democracia, realizam as eleições com os quatro métodos acima, e comparam resultados.

O primeiro método dá vitória ao A, preferido de quatro habitantes, vence os demais, cujas preferências são três, dois e um. O segundo método selecionaria o A e o B para um segundo turno, e podemos ver que o B vence o A na preferência dos eleitores que não votariam inicialmente neles, o que daria a vitória ao B em uma eleição a dois turnos.

Contando os pontos pelo terceiro método, teríamos o A com 20 pontos, o B com 21 pontos, o C com 25 pontos e o D com 24 pontos, sendo a vitória por pontos corridos claramente do candidato C. Se contarmos os confrontos, o A vence apenas 12 confrontos (4 vezes cada candidato), o B vence 15 (6 vezes o A, 6 vezes o C e 3 vezes o D), o C vence 16 (6 o A, 4 o B, 6 o D) e o candidato D vence 17 (6 o A, 7 o B e 4 o C) confrontos, sendo claro que a vitória pertence ao candidato D. Pequenolândia terá, como resultado de sua eleição, anarquia completa.

Esse pequeno exemplo ilustra como métodos reconhecidos e consagrados pelo uso na democracia não apenas geram resultados diferentes, eles determinam o vencedor. Cada método elegeu um candidato, e nenhum deles pode ser acusado de ser injusto, todos são usados em eleições, campeonatos e torneios.

Uma resposta otimista seria admitir que existe um método correto e justo, apenas que não é um desses que listei; mas os matemáticos já se encarregaram de arrasar esse otimismo com um sonoro não. O teorema da impossibilidade de Arrow afirma que quaisquer critérios justos que sejam escolhidos, com hipóteses matemáticas exatas de o que ele chama de justiça (todos os critérios acima satisfazem as hipóteses de Arrow), sempre é possível encontrar uma lista de preferências que eleja dois candidatos diferentes com métodos justos. De forma simplificada, nenhuma eleição é justa, Pequenolândia terá que escolher um método antes de escolher um presidente (diferentemente do Brasil em 1988). Em outras palavras, é impossível, de uma lista genérica de preferências, obter de forma inequívoca quem será o presidente.

Em um exemplo atual, e mais concreto, este artigo (agradecimentos a Guilherme Mazanti pelo link), infelizmente em francês, atesta um fato surpreendente. Nessas eleições francesas, o candidato François Bayrou, quinto colocado no primeiro turno, ganharia de qualquer oponente em um combate direito (4˚ método); se participasse, ele ganharia qualquer segundo turno! Ora, como pode um candidato preferido por toda a população a qualquer outra opção não apenas não ser o presidente, mas ser quinto lugar nas pesquisas? Eis um dos resultados impressionantes do teorema de Arrow, colocando em uma perspectiva diferente a afirmação de meu amigo, até que não deve ser tão difícil encontrar eleições mais justas que aquelas que não elegem o favorito da população frente a qualquer outra opção.

Ainda, quanto a meu amigo francês, ele pode ficar tranquilo. Diz-se que eleições justas são pleonasmo, pois se não fosse justa não seria eleição; Arrow nos garante, nada de pleonasmo, eleições justas são, na realidade, um paradoxo.

5 respostas

O melhor remédio

Rookie

No post anterior sobre motores moleculares, comentei um aparente paradoxo estatístico com aplicações fascinantes na biofísica. Esse tipo de fenômeno, contra-intuitivo e profundamente aplicado, não é tão raro quanto se imagina. Se o paradoxo de Parrondo é meu favorito, dedico o post de hoje a meu segundo paradoxo aparente favorito, que começa em uma manhã repleta de problemas.

Você acorda sentindo dores nas costas, que aumentam em ondas, até se tornarem as piores que você já experimentou se não deu a luz a uma criança ou teve uma parada cardíaca. Você é levado às pressas ao hospital, onde o médico prontamente diagnostica um caso clássico de pedra do rim, e você se arrepende de todo aquele sal grosso que adora na picanha. Felizmente há cura, e o médico logo iniciará o tratamento, mas, antes, precisa de seu consentimento para saber qual procedimento tomará. Ele apresenta as opções, enquanto você agoniza de dor.

Há dois tratamentos possíveis, o A e o B. Um estudo foi realizado para testar a eficácia dos tratamentos e determinar qual é o melhor e você, como bom amante das exatas, pede para ver os dados dos estudos. Ele é dividido em casos de pedras grandes e pedras pequenas, sendo o número total de casos o mesmo testado no tratamento A e B, para que não haja tendências.

No caso das pedras grandes, o tratamento A é mais eficaz que o B. Ele curou 190 dos 260 testados (73%) enquanto o B curou apenas 50 dos 80 casos testados (62,5%). Sendo 73%>62,5%, o médico recomenda, caso você tenha uma pedra grande, aceitar o tratamento A.

No caso das pedras pequenas, o tratamento A também é mais eficaz que o B. Ele curou 80 dos 90 casos testados (88,8%) enquanto o B curou apenas 230 dos 270 testados (81,2%). Como 88,8%>81,2%, o médico recomenda, caso você tenha uma pedra pequena, aceitar o tratamento A. Ainda, ele pergunta qual tratamento você escolhe.

A questão parece estúpida, pois o tratamento A é mais eficaz que o B em todos os casos. No entanto, você, em um lampejo de lucidez em meio à dor, nota algo. Em ambos os tratamentos, 350 casos foram testados. O A curou (190+80=) 270 casos de seus 350, enquanto o B curou… (50+230=) 280. Sem sombra de dúvida, o médico deveria recomendar o mais eficaz dos tratamentos, que seria, sem hesitação, o tratamento B.

Consternado, você pode pensar que o tratamento B é melhor caso você não saiba seu tipo de pedra, e o A caso saiba; mas rapidamente percebe que esse raciocínio é profundamente desonesto. Você pode apenas ter uma pedra grande ou pequena e, na sua lógica, se souber que tem a grande, tomará o A; se souber que tem a pequena, também tomará o A. Seu conhecimento da pedra em nada influenciará sua decisão, e você ainda sabe que o B curou mais que o A nos dois casos juntos, o problema persiste.

Eis o famoso paradoxo de Simpson, uma armadilha clássica na teoria de probabilidades que atinge até os mais preparados. Temos uma tendência instintiva a achar que medidas que beneficiam todos os grupos envolvidos serão benéficas ao coletivo, isso não é necessariamente verdade. Esse paradoxo aparece de diversas formas nas análises estatísticas, como, por exemplo, a comparação entre Chicago e Illinois nas matérias de matemática, com uma análise mais profunda nos grupos étnicos e sociais. Chicago foi melhor que Illinois em todos os grupos étnicos analisados (brancos, negros, hispânicos), mas ao final Chicago ficou muito aquém de Illinois nos resultados. Isso aconteceu apenas porque a distribuição racial das regiões diferia bastante, criando esse aparente paradoxo.

A razão desse paradoxo, esse aparente contrassenso, é a diferença no tamanho das amostras. No caso da pedra no rim, podemos ver que pacientes com pedras pequenas tendem a sistematicamente receber o tratamento B, enquanto pacientes de pedras grandes tendem a receber o tratamento A. Mas, mais importante que a diferença no tamanho das amostras, temos que o fator “pedra grande” ou “pedra pequena” influencia muito mais a taxa de cura que o tratamento usado. O paradoxo de Simpson ocorrendo é um excelente indício de que há uma variável escondida, algum fator determinante ao dividir o estudo em grupos e que, somados os grupos, desaparece.

Não podemos dizer que o estudo apresentado a você no hospital possui “estatística que não presta”, mas devemos tomar cuidado na análise. O paradoxo de Simpson é uma das melhores maneiras de enganar alguém com estatísticas, então não se deixe levar por estatísticos malandros; o todo é mais que a soma das partes, frações às vezes enganam e, escolhendo o tratamento A ou B, sempre beba bastante água.

Mas, já que apresentei a situação, deixo a pergunta: e você? Qual tratamento escolheria?

1 resposta

No cassino de Parrondo

Geek Rookie

A estatística possui alguns resultados não muito intuitivos, e muito divertidos. Um deles, proposto pelo físico espanhol Juan Parrondo, é um de meus favoritos. Para contar esse aparente paradoxo, convido-os a jogarem um jogo no cassino de Parrondo.

Esse cassino possui duas mesas, uma com um jogo A, outra com um jogo B, que possuem regras diferentes. Em ambos os jogos você só pode apostar uma ficha por vez, digamos, valendo R$100,00. Se você ganhar, leva mais uma ficha consigo. Se perder, perde sua ficha.

No jogo A você deve tirar uma carta de um baralho muito bem embaralhado. Se a carta for preta, você ganha. Se for vermelha, você perde. Neste maço de baralho, contudo, há um curinga; e você perde se tirar o curinga.

No jogo B, as regras mudam um pouco. Se seu número atual de fichas não for um múltiplo de três, suas chances são ótimas: você tira uma carta e perde apenas se ela for de copas ou o curinga. No entanto, se seu número de fichas for múltiplo de três, você deve tirar um às ou o curinga para ganhar, perdendo em todos os outros casos.

Não é surpresa nenhuma se eu te contar que o jogo A é falência na certa. A chance de você perder é maior que a de ganhar, e o ganho é igual à perda; jogar diversas vezes seguidas o jogo A fará você sair do cassino de mãos vazias. E apesar de o jogo B parecer um grande negócio, ele não é, podemos provar com diversas simulações numéricas, o que é o equivalente a jogar várias vezes, que a tendência é perder mais e mais dinheiro jogando o jogo B várias vezes. Assim, nas mesas do cassino de Parrondo a casa sempre vence.

Mas suponha que você pode caminhar de uma mesa à outra. Ora, certamente você só iria ao jogo B quando tem certeza de que suas fichas não são um múltiplo de três; o cassino jamais permitira algo parecido. Então você pode mudar de uma mesa para outra, mas com uma regra: você não pode contar suas fichas. Para deixar ainda mais justo, você não sabe, a cada aposta, se ganha ou perde, fica apenas sabendo o resultado final de suas aventuras ao sair do cassino. Assim, você até pode alternar os jogos, mas, sem contar as fichas e sem saber quando ganha ou perde, não consegue tirar muita vantagem disso. De certa forma, é como se você fosse obrigado a, na entrada, dizer quantas vezes irá apostar em cada jogo e em qual ordem. Assim, nunca sabendo em qual você ganha e qual perde, não poderá mudar de estratégia no meio da noite.

E eis a parte surpreendente. O jogo A é perda certa para você, o B também se jogado continuamente; mas alternar os jogos te leva a ganhar muito dinheiro. Esse fenômeno é o paradoxo aparente de Parrondo, duas táticas fracassadas que, combinadas, resultam em um ganho certeiro. Aos que não acreditam em mim, escrevi um pequeno código de computador para simular esses jogos todos. Claro, um exemplo não prova nada, coloco o resultado apenas para que sua confiança em mim aumente. O jogo A+B consiste em escolher, antes de cada jogada, aleatoriamente um dos jogos, ambos com a mesma probabilidade, como se tirasse no cara-ou-coroa a mesa escolhida para apostar. Eis os resultados, começando com uma fortuna de 47 fichas e permitindo ficar no negativo:

E esse aparente paradoxo nada mais é que um fenômeno estatístico fascinante usado abundantemente em diversos sistemas biológicos, o que inclui suas células. Temos, no caso de Parrondo, um jogo que apenas “bagunça” seu dinheiro (o jogo A, cuja chance é quase 1/2 para cada lado) e outro que te permite ganhar bastante, até atingir um valor (o múltiplo de três) bem difícil de atravessar, tão difícil que é mais fácil o jogo te fazer perder dinheiro a atravessar aquele valor e, perdendo, ele encontrará outro múltiplo de três, e será mais uma vez difícil de subir. No entanto, esse combo “bagunça+tendência” torna-se uma tática interessante, pois a bagunça pode te permitir “saltar” os múltiplos de três e, fora deles, você escala mais fácil a escada da fortuna.

 A partir desse ponto, esse post torna-se geek. Continue por sua conta em risco.

Parrondo não estudava teoria dos jogos, estudava os chamados “motores moleculares”, a base do funcionamento de diversos processos biológicos no nível celular. Suponha uma partícula submetida a um potencial da forma “dente de serra”:

Dente de serra

E suponha essa partícula com uma temperatura suficientemente baixa (ou seja, suficientemente lenta) para que fique confinada no poço. Na figura, o roxo representa a densidade de probabilidade da posição dela, note que é bem difícil ela sair daquele lugar.

Mas suponha agora que eu aumente bastante a temperatura, bastante mesmo. Ora, a partícula se comportará como se ignorando o potencial, e as chances de ir para a esquerda e para a direita tornam-se as mesmas. Mas algo é diferente, se pensarmos em qual poço é mais provável que ela caia. Veja como é a evolução desse sistema, nessa figura:

parrondo_4

Note que, no momento de alta temperatura, é mais provável que ela tombe no poço da direita (área verde) que no poço da esquerda (área vermelha). Ao resfriarmos o sistema, que é representado pelo terceiro quadro, percebemos que a partícula tende a andar pela serra para a direita. Por causa da assimetria do potencial, o sistema adquire uma direção preferencial.

A relação disso com o cassino é simples, o jogo B é a situação de temperatura baixa e o jogo A é a alta temperatura, andar para a direita significa ganhar dinheiro e perder dinheiro é andar para a esquerda. Mas o cassino de Parrondo é malandro, nele os picos de potencial não são iguais e o jogo B tende a te empurrar para a esquerda, e o jogo A também (o que seria equivalente a uma gaussiana levemente assimétrica). No entanto, pela diferença na inclinação do potencial, passar ao jogo A e voltar ao B torna o sistema mais propenso a te mandar para a direita, a direção de maior fortuna!

Esse jogo de aumento e diminuição de temperatura é a base dos motores moleculares, ele é a razão pela qual a proteína é sintetizada pelo ribossomo em um sentido e não decide, aleatoriamente, seguir o sentido oposto e ir se desfazendo. E a célula funciona, vive, produz e sintetiza proteína dessa maneira: aumento de temperatura, diminuição, aumento (o que deve explicar aquele monte de ATP sendo desfeito para fazer esse sistema andar), em um intrincado maquinário de potenciais assimétricos que nos permite andar, pensar, respirar e jogar cartas em um cassino.

3 respostas

Um diagrama nada claro

Rookie

Na faculdade, aprendemos a física por sua trajetória histórica: começamos pelas leis de Newton, sua mecânica, passamos ao estudo de ondas, óptica, termodinâmica, atravessamos o eletromagnetismo e terminamos a “física básica” com quântica. Mais para o final do curso, continuamos com a física do século XX, da qual a quântica faz parte, além de incluir a física estatística e a relatividade geral nessa história. Matérias mais avançadas, como a teoria quântica de campos (TQC) e a teoria estatística de campos (TEC) são assunto de mestrado e doutorado, muita gente parece viver bem feliz sem jamais tocar em um livro de qualquer dessas matérias.

Mas a relação entre as áreas da física não é essa histórica, uma não leva naturalmente a outra. É possível ser muito feliz em uma área da física sem jamais precisar se aprofundar muito em outra (ainda que grandes descobertas costumem ser feitas apenas por físicos com um vasto conhecimento de quase todas as áreas), não preciso saber astronomia para trabalhar com física do estado sólido (ou física dos materiais).

Então decidi tomar alguns minutos, sentar e pensar em um diagrama mais compreensivo da física, que leve em conta as interconexões entre as áreas e que seja uma divisão justa e organizada dessa ciência. É evidente que cheguei a algo bem confuso, mas o resultado não ficou feio, e coloco-o aqui.

Muitos físicos vão discordar com ferocidade da divisão e organização, mas foi o melhor que pude, não conheço tanto de todas as áreas para entrar em uma reflexão mais profunda que o que escrevo nesse post.

Comecei colocando a matemática como centro. A física é inteira apoiada na matemática, e nela estão muitos dos vínculos das áreas da física. Em seguida, tracei as três principais áreas da física: relatividade (geral ou restrita), física estatística e física quântica.

Física quântica: é o estudo do muito pequeno, muito mesmo. Estamos falando de elétrons, prótons, átomos, nada que possamos ver ou tocar diretamente, precisamos estar pelo menos a 0,00001 mm ($10^{-8}$m) para começar a sentir algum efeito dos estudos dessa área. Ainda, é o que precisamos estudar para entender do que as coisas são feitas, como fazer coisas novas, materiais novos, entender as leis que regem a escala atômica e usá-las.

Relatividade: estudamos os efeitos de velocidades muito altas (próximas às da luz, que é a máxima possível), massas muito grandes (como a da Terra ou a do Sol) e energias muito elevadas (como a explosão de uma estrela).

Física estatística: é a área que tenta deduzir, a partir do mundo do muito pequeno, o que acontecerá no nosso mundo. Tentamos entender como a gota de água tende a ficar junta se ela é feita de várias moléculas, ou como não conseguimos atravessar a parede se o espaço entre os átomos é muito maior que os átomos.

Assim, posso explorar as intersecções entre essas áreas. Se estamos na fronteira entre relatividade e quântica, estamos falando da teoria quântica de campos (TQC), uma área bem complicada que tenta escrever a mecânica quântica em uma linguagem que leve a relatividade em conta. Não me atrevo a tentar misturar relatividade geral com quântica, ninguém consegue fazer isso decentemente. Entre a física estatística e a quântica, teremos a teoria estatística de campos (TEC), que usa diversas propriedades do mundo do muito pequeno para explicar muito fenômenos do nosso cotidiano, em uma linguagem matemática bem trabalhada e bem parecida com a da TQC. Eu poderia colocar tudo em uma área só, campos, mas assim fica mais fácil de ver.

Entre a relatividade e a física estatística, temos a astrofísica, o estudo das propriedades físicas das estrelas, galáxias, que exige tanto conhecimento de relatividade, por reger as leis fundamentais desses corpos, como conhecimentos da física estatística, porque uma estrela é formada de muitos átomos e uma galáxia de muitas estrelas. A relatividade, sozinha, inclui a nossa querida mecânica do colegial, que é apenas um caso particular da relatividade para baixar velocidades e massas suficientemente pequenas. A física estatística, quando aplicada a gases e líquidos, torna-se a termodinâmica.

Se continuamos, podemos pensar que o estudo das propriedades físicas dos corpos celestes aliado às leis de Newton nos permite saber a posição, trajetória e diversas outras grandezas estudadas pela astronomia. A astrofísica, quando estudada em grande escala e recebendo o apoio das leis da termodinâmica e da física estatística, torna-se a cosmologia: o estudo do universo como um todo, sua expansão, evolução e destino. Aplicar a teoria estatística de campos à termodinâmica nos torna capazes de descrever estruturas mais complexas que gases, podemos até pensar em cristais, coloides, plásticos, estamos na física do estado sólido. A teoria quântica de campos e a teoria estatística de campos se encontram para descrever propriedades complicadas do mundo subatômico, permitindo-nos estudar a física de partículas. Por fim, a teoria quântica de campos, capaz de descrever os elétrons e os prótons (que possuem carga) e a mecânica de Newton se encontram no eletromagnetismo.

Por fim, podemos colocar algumas outras áreas. O eletromagnetismo é muitas vezes estudado profundamente no aspecto de transmissão de energia eletromagnética em forma de onda, uma área conhecida como óptica, que engloba toda a propagação de ondas eletromagnéticas no vácuo ou não. A física do estado sólido e a de partículas se encontram para tentar gerar materiais novos, diferentes, estruturas moleculares complicadas, e podemos atribuir esse estudo à química molecular, que não é tanto física assim, mas merecia um lugar no diagrama. As partículas e o eletromagnetismo juntam forças para desbravar os mistérios do centro do átomo, em uma área muito ativa no último século chamada física nuclear. E das partículas, sozinha e um pouco isolada, quase uma sub-área da matemática, parte a teoria das cordas.

Qual a lógica do diagrama? Se você quiser estudar alguma área, terá que saber bastante de todas as áreas internas à que escolheu, estudando todas as que sua área toca no anel interior. Claro, isso não torna as áreas exteriores mais difíceis, você muitas vezes não precisa se especializar nas áreas interiores para saber a sua, é apenas um diagrama que indica vínculo, procedência e contato entre as áreas. Queria que o diagrama terminasse com um anel completo, mas não consegui pensar em nada que viesse de estado sólido e cosmologia, ou nada melhor para colocar entre astronomia e cosmologia que “coisas do espaço”.

4 respostas