Sempre fico feliz quando uma notícia da física atinge o grande público, quando a mídia decide que algum descoberta forma uma frase de efeito digna de manchete, e nessa semana não foi diferente. Um grupo de físicos do Instituto Max Planck conseguiu criar um gás a temperatura negativa, abaixo do zero absoluto, e isso provocou manchetes muitas vezes enganosas e, apesar de algumas matérias terem saído interessantes, a maior parte era apenas um agregado de traduções de versões americanas feitas por quem não entende do assunto.
Temperaturas negativas não são novidade na física, elas têm até página na Wikipédia, e pretendo hoje, nesse post, tentar explicar o que queremos dizer com isso, e tentar esclarecer confusões lançadas pelas matérias sensacionalistas de física de folhetim. Para isso, precisamos entender o que é temperatura.
No princípio hesitei se poderia explicar esse tópico sem antes falar de um conceito fundamental da termodinâmica, e de toda a física, a entropia. Temia descobrir, enquanto escrevia, que eu mesmo não entendia o assunto, pois é uma das noções mais escorregadias da ciência. De forma extremamente simplificada, entropia é a medida da desorganização de um sistema. Preciso de um exemplo tão simplificado quanto minha explicação, vou usar um sistema a dois níveis de energia. Dificilmente encontramos algo na vida real que seja isso, mas pouco importa, quero apenas explicar o conceito. Imagine um sistema com $N$ partículas, sendo cada partícula capaz de estar em um estado de energia zero ou em um estado de energia $\varepsilon$.
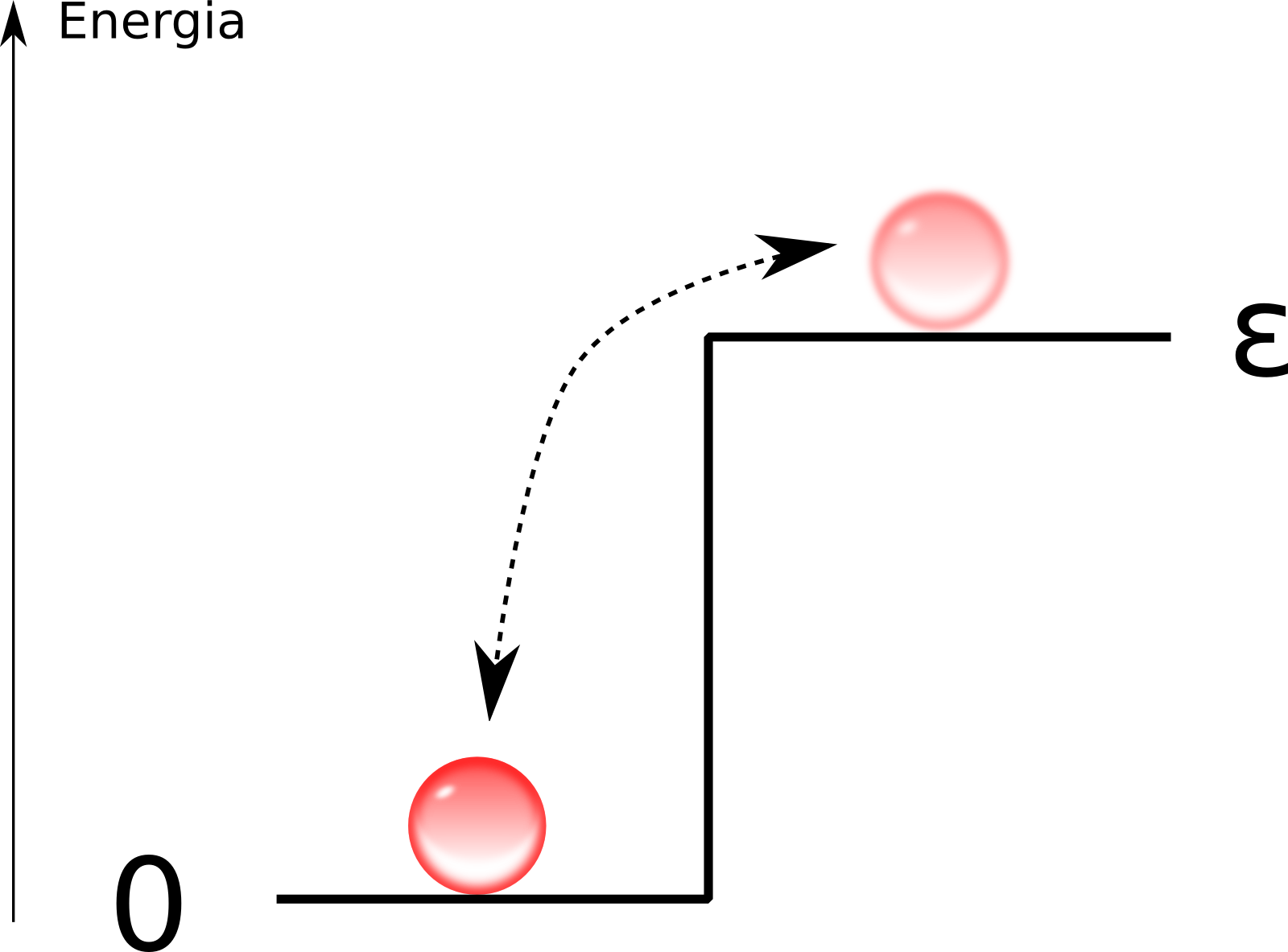 Se todas as bolinhas estiverem confinadas no estado zero, esse sistema tem entropia zero. Se todas estiverem confinadas no estado $\varepsilon$, o sistema também terá entropia zero. Mas se elas puderem se mexer, variar de um estado a outro, essa entropia será um valor maior, e positivo, indicando que o sistema não mais possui aquela ordem perfeita de antes e agora é uma mistura estranha de estados. A entropia indica quão bem feita é essa mistura, sendo máxima quando todas as configurações do sistema, todas as combinações de bolinhas em cima e embaixo, são possíveis e igualmente prováveis, ou seja, desordem completa, não posso afirmar nada sobre o estado atual do sistema, ele pode ser qualquer coisa.
Se todas as bolinhas estiverem confinadas no estado zero, esse sistema tem entropia zero. Se todas estiverem confinadas no estado $\varepsilon$, o sistema também terá entropia zero. Mas se elas puderem se mexer, variar de um estado a outro, essa entropia será um valor maior, e positivo, indicando que o sistema não mais possui aquela ordem perfeita de antes e agora é uma mistura estranha de estados. A entropia indica quão bem feita é essa mistura, sendo máxima quando todas as configurações do sistema, todas as combinações de bolinhas em cima e embaixo, são possíveis e igualmente prováveis, ou seja, desordem completa, não posso afirmar nada sobre o estado atual do sistema, ele pode ser qualquer coisa.
A temperatura é a medida de quanto a entropia de um sistema varia quando damos energia a ele: quanto menor a temperatura, mais desorganizado um sistema fica com energia. Naturalmente, quanto maior for a temperatura, menos desordem um sistema ganha com a energia.
O fato da temperatura ser sempre positiva em nosso cotidiano é um reflexo da propriedade natural do aumento de entropia com o aumento de energia, como arrumar sua casa perfeitamente e lançar dentro dela uma ratazana raivosa, o equivalente da energia; dificilmente a casa ficará ainda mais organizada. Assim, apesar de sistemas com alta temperatura ganharem pouca entropia com energia, eles não perdem entropia.
Se deixamos nosso sistema de bolinhas a dois níveis interagir com o meio externo, ele poderá trocar energia com o meio e as bolinhas ganham ainda mais liberdade de subir e descer a ladeira. Se o sistema e o meio externo são muito diferentes quando entram em contato, eles vão trocar energia até que o quanto um sistema é desordenado pelo ganho de energia seja igual ao quanto o outro também é, ou seja, até que as temperaturas sejam iguais.
Isso é reflexo do princípio de máxima entropia, uma noção física que vai além das bolinhas e partículas, ligada profundamente a teoria da informação e probabilidades. Mais uma vez de forma bem simplificada, ele diz que, se você não tem uma boa razão para proibir um estado, o sistema atingirá esse estado e, se não tem uma boa razão para diferenciar dois estados, o sistema atingirá os dois com a mesma probabilidade. Em nosso problema das bolinhas, o sistema trocará energia com o meio externo até que o quanto ele causaria de desordem cedendo energia seja igual ao quanto ele ganharia de desordem ganhando energia, porque dessa maneira a entropia do processo todo (sistema + meio externo) será a máxima possível. Dessa forma, quando as temperaturas são iguais, isso significa que tanto o conjunto sistema + meio externo pode ocupar o maior número de estados possíveis de energia.
Como um gás lançado em uma sala vazia tende a se dispersar, não a se concentrar, porque eu não tenho uma boa razão para impedi-lo de ir para qualquer lugar da sala. Ele tende a ocupar todo o espaço e a chance de encontrar uma partícula em qualquer lugar é a mesma: isso é o princípio da máxima entropia. Se você conectar essa sala a uma outra vazia, pouco a pouco o gás vai ocupando também a outra sala até que todos os estados possíveis sejam ocupados com a mesma probabilidade.

Pelo princípio da máxima entropia, o gás tende a invadir a segunda sala e ocupar todo o espaço. A probabilidade de que ele fique todo na primeira sala é infinitamente pequena.
Se deixamos o sistema acoplado ao meio externo em uma temperatura fixa, ele trocará energia com o meio externo, e a temperatura será o quanto de desordem ele vai ganhar quando ganha energia. Se essa temperatura é baixa, o sistema ganha muita entropia com um pouco de energia. Isso acontece em situações como a de haver todas as bolinhas paradas na posição 0. Dar um pouco de energia significa permitir alguns saltos para o andar de cima, isso bagunçaria o sistema dando bastante entropia a ele. Se o sistema está em alta temperatura, como no caso de um gás quente, dar ainda mais energia não bagunçaria tanto o sistema.
Podemos escrever isso com alguma matemática. A chance de uma daquelas bolinhas estar em um estado de energia $E$ é dada por $\frac{e^{-E/T}}{Z}$, onde $e$ é um número especial entre 2 e 3 e $Z$ é alguém que multiplicamos para que a probabilidade não seja maior que 1 (para quem começou a ver física estatística, essa é a distribuição de Boltzmann!). É fácil ver que a chance de estar no estado de energia 0 é $1/Z$, enquanto a chance de estar no estado $\varepsilon$ é $\frac{e^{-\varepsilon /T}}{Z}$. Isso representa um fato físico famoso: é mais fácil estar em um estado de baixa energia que em um de alta energia. Quanto menor a temperatura, mais difícil é encontrar alguém em um estado de energia alta. Quanto maior a temperatura, mais ambos os estados ficam com probabilidades parecidas. A maior parte dos sistemas físicos funciona dessa exata maneira.
No entanto, se você conseguir ser malandro, como os físicos do Instituto Max Planck, e criar um sistema físico bem patológico tal que estados de energia mais alta são mais prováveis, como você explica usando esse formalismo? Ora, basta dizer que são estados a temperatura negativa. Dessa forma, $\frac{e^{-\varepsilon /T}}{Z}>1/Z$ e você consegue continuar a trabalhar com esses sistemas usando sua matemática favorita.
É porque associamos temperatura a essa taxa de ganho de desordem que podemos interpretar desse jeito estranho. Temperatura não é mais o movimento das partículas, isso ficou com os gases ideais no colegial, ela agora é a medida do ganho da desordem em função da energia. E se um sistema começa a privilegiar estados de energia alta, interpretamos isso como uma temperatura negativa.
Ouvi muito a respeito, inclusive da Wikipédia, sobre a temperatura negativa ser o limite de uma temperatura tão positiva que ela “dá a volta” e vira negativa. Como dizer que os reais são um corpo cíclico me causa urticária, tento explicar o que isso significa. Uma temperatura muito baixa favorece muito estados de baixa energia. Uma temperatura alta não favorece ninguém, e quanto mais alta, menos favorecimento possui. Se atingíssemos a temperatura $+\infty$, teríamos passado de uma situação de favorecimento das energia baixas a não favorecer ninguém. Se fôssemos “além” do $+\infty$, teríamos uma situação que privilegia as altas energias, e é isso que aquela explicação estranha quer dizer. Não gosto dela, e paro a explicação da explicação por aqui.
Resumindo: os cientistas do Instituto Max Planck conseguiram criar um sistema patológico o suficiente para deixar os estados de alta energia mais prováveis que os de baixa energia. Na matemática da física estatística, isso é interpretado como uma temperatura negativa, pois temperatura é o que mede essa preferência por estados de baixa energia. Isso não é nada chocante ou escandaloso, é interessante que eles tenham conseguido isso para um sistema quântico bem complicado, o artigo original está aqui, mas, infelizmente, é mais uma manchete para vender jornal que um grande avanço para a termodinâmica.
Assumo que o post ficou confuso, mas é um tema complicado. Um dia sento e escrevo algo mais claro sobre entropia, no mesmo dia em que tomar coragem para ler a montanha de textos a respeito da interpretação física dela. Precisaria selecionar, ler, escrever, revisar tanta coisa que, em matéria de desordem, deixo exatamente como está.