Arquivo do autor:Ricardo Marino

Sobre Ricardo Marino

Físico, estatístico, brasileiro, um pouco francês, falador, curioso, aperta a pasta de dente pelo meio e começa a comer coxinha pela base, que é o único lado certo de fazê-lo.

Epidemias, parte I

Hardcore

Trombei esses dias com um artigo de 2001 sobre propagação de vírus em humanos e sua comparação a vírus de internet. O estudo da disseminação de infecções é velho na física, diversos modelos de epidemias são estudados e muitos com resultados razoavelmente bons. Um ponto comum em modelos estudados pela epidemiologia é a noção de threshold, ou seja, o valor mínimo de eficiência que uma infecção deve ter para conseguir se propagar. Novamente, esse é um post hardcore, os corajosos sigam-me, vamos ver com cuidado como isso funciona.

Esse post ficou grande, então parti em dois. Nesse primeiro, comento o modelo de propagação de vírus em seres humanos, no próximo trato da internet.

Representamos indivíduos como pontos e o contato entre indivíduos como linhas em um grande grafo. Passamos a nos perguntar qual seria um modelo eficaz de grafo para modelizar as relações humanas. Certamente não conhecemos pessoas aleatoriamente na rua, costumamos conhecer melhor nossos vizinhos, familiares e colegas de trabalho, que por sua vez conhecem-se. Um jeito legal de modelizar essa ideia, que chamamos de grafo de small world, é tomar um anel de pontos, sendo cada ponto ligado a seus $ m$ vizinhos mais próximos. Em seguida, passamos “em revista” essas conexões da seguinte forma: cada ponto terá uma probabilidade $ p$ de desfazer uma conexão com um vizinho seu no sentido horário e associá-la a algum outro ponto aleatoriamente. A ideia do sentido horário é apenas para evitar mexer na mesma conexão duas vezes. Se $ p=1$, essa revista resulta em um grafo em forma de anel com conexões completamente aleatórias. Se $ p=0$, o grafo continuará no modelo do conhecimento apenas da vizinhança, mas, se $ p$ é pequeno, o grafo tornar-se-á um modelo muito próximo do que queremos: vizinhos possuem uma chance maior de se conhecerem do que conhecerem alguém do outro lado do grafo, mas de vez em quando algum vizinho seu conhece alguém lá longe, o que é bem coerente com a realidade e até permite aquelas coincidências do tipo “hoje meu avô almoçou com o pai de um professor meu”.

O resultado está bem representado nessa figura, onde os pontos são inicialmente ligados a seus $ 2m$ vizinhos mais próximos, com $ m=2$. É o famoso modelo de Watts-Strogatz, ou modelo de small-world:

Podemos, com esse modelo bonitinho, estudar a propagação de infecções entre seres humanos. Imaginemos um vírus que, a cada contato entre são e infectado, tenha uma probabilidade $ nu$ de contágio e, a cada “turno”, tenha uma probabilidade $ \delta$ de cura de um infectado. A chance de um ponto possuir $ k$ vínculos é $ P(k)= \frac{1}{\langle k\rangle}e^{-k/\langle k\rangle}$ nesse modelo, e $ \langle k\rangle=2m$. A equação estocástica dessa criança não é bonita, então vamos usar um mean field, calcular o que vai acontecer com a densidade média de infectados supondo que todos os pontos possuem o mesmo número de conexões, $ 2m$, naturalmente, e que todos estão ligados a um número de infectados igual ao valor médio de infectados, essas são as características de uma abordagem de campo médio. A densidade total de infectados, denotada $ \rho_t$ por ser uma função do tempo, é apenas o número total de infectados dividido pelo número total de pessoas. Diremos que a variação na densidade de infectados $ \rho_t$ (a fração da população infectada naquela “rodada”), que toma valores entre 0 e 1, perde a cada “rodada” o equivalente a $ \delta\rho_t$ (os que se curaram) e ganha o equivalente ao contato são-infectado, que é $ nu\langle k\rangle\rho_t(1-\rho_t)$, ou seja, chance de um contato ser são-infectado $ \rho_t(1-\rho_t)$ multiplicada pelo número médio de contatos $ \langle k\rangle$ e pela chance de esse contato transmitir a infecção $ \nu$. Dividindo a equação toda por $ \delta$ e sem precisar ir muito além de uma reparametrização no tempo, podemos escrever:

\[\frac{d}{dt}\rho_t=-\rho_t+\lambda\langle k\rangle\rho_t(1-\rho_t).\]

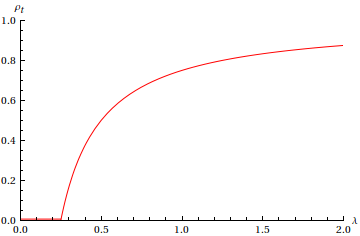
Com $ \lambda= \frac{\nu}{\delta}$ o valor que interessa para medir a eficácia de uma infecção. E essa equação, ainda que seja apenas uma teoria de campo médio, já nos dá bastante informação sobre o que está acontecendo. Você até pode pedir para o Wolfram Alpha resolver essa para você, eu não faria diferente, mas vale mais estudar algumas propriedades na mão. Chamamos densidade de persistência o valor de $ rho_t$ para o qual sua derivada temporal é zero. Se ela não é nula, temos uma infecção persistente em uma fração da população. Igualando a equação acima a zero, percebemos duas respostas possíveis: ou $ rho_t = 0$, ou $ \rho_t=1- \frac{1}{\lambda\langle k\rangle}$. Como a densidade de infectados não pode ser menor que 0, naturalmente, descobrimos que, se $ \lambda < \frac{1}{\langle k\rangle}$, então a única solução possível é $ \rho_t=0$, pois a segunda solução fica absurda. Mas, se a infecção é mais eficaz que o threshold $ \frac{1}{\langle k\rangle}$, teremos um crescimento da densidade de persistência que tende a 1 quando $ \lambda$ se aproxima do infinito.

Densidade de persistência com m=2.

E fica claro que o threshold, dependendo do inverso do número médio de contatos, que nesse modelo é proporcional ao número de vizinhos, nos dá uma informação esperada: quanto maior o número de vizinhos (contatos), menos eficaz uma doença deve ser para se propagar. Se uma doença é bem eficaz, podemos reduzir seu impacto com uma diminuição nos vizinhos, se está com gripe, não saia de casa.

Esse modelo é bem coerente com diversas observações de epidemias simples em populações. Por esse mecanismo de small-world, apenas doenças suficientemente poderosas, com eficácia $ \lambda$ maior que um determinado limite, podem se propagar pela população, possuem vida no longo prazo. A mudança de fase ocorre no threshold $ \lambda^\star= \frac{1}{\langle k\rangle}$ que, no gráfico acima, ocorre em $ \lambda = 0,25$. O próximo passo nesse modelo seria estudar um grafo em que pessoas podem morrer, nascer, tornar-se imunes, tomarem vacinas ou tornarem-se mais suscetíveis a doenças com o tempo.

Tudo isso é muito interessante, mas não consegue explicar a propagação de vírus na internet. Em um próximo post, veremos que, na internet, small-world não pode ser aplicado (afinal, todos conhecem o Google ou o Facebook) e a própria noção de threshold, por um fenômeno estatístico fascinante, desaparece.

2 respostas

Prova surpresa

Geek Hardcore Rookie

O post de hoje não é muito informativo, é mais perturbador, um probleminha de lógica para não deixar você dormir.

Um professor chega à aula e avisa sua classe que aplicará, no mês de abril, uma prova surpresa. Um aluno, que futuramente se tornaria matemático na área de lógica, pergunta o que o professor entende por surpresa. Estranhando a pergunta, o professor responde que uma prova surpresa é uma prova tal que, no início de cada dia do mês de abril, os alunos não podem deduzir ou saber que a prova será aplicada naquele dia. Triunfante, o aluno conclui que não haverá prova nenhuma, pois:

– Se a prova não for aplicada até o 30 de abril, então ela terá que necessariamente ser nesse dia e, no começo do dia, já não será surpresa. Então o 30 de abril não pode ser a data da prova.

– Se a prova não for aplicada até o 29 de abril, então ela terá que ser necessariamente nesse dia, pois o 30 está excluído. Mas, assim sendo, ela não será uma surpresa, então o dia 29 não pode ser o dia da prova.

– Se a prova não for aplicada até o 28 de abril, então ela terá que ser necessariamente nesse dia, pois o 30 e o 29 estão excluídos. Mas, assim sendo, ela não será uma surpresa, então o dia 28 não pode ser o dia da prova. E assim por diante, ele exclui todos os dias.

No dia 12, ele recebe a prova. Onde ele errou?

7 respostas

O problema da diretora do colégio

Geek

Venho por meio deste compartilhar um problema deveras interessante que requereu algumas horas do meu dia para a programação. Escrevi-o há algum tempo a um amigo cursando ciência da computação que, sendo garoto de programa, certamente saberia apreciar o que fiz, e sou carente desse tipo de apreciação. O problema que me foi proposto em meu curso de física estatística foi o da diretora do colégio.

Aconteceu uma vez comigo, recebi, acho que na sexta série, um papel para escrever os nomes dos coleguinhas com que gostaria de estar ano seguinte. Escrevi os dois nomes que queria (era uma criança sozinha e com poucos amigos), entreguei e no ano seguinte estava na sala deles. Ainda, as salas não mudaram muito, o que é razoável, já que as pessoas tendiam a querer ficar com quem já estavam, achei que a diretora havia atendido aos pedidos individualmente, mas hoje penso que não. Vamos tentar entender a razão de, se a diretora fosse realmente levar aqueles papéis a sério, ela teria que aprender um pouco mais de física e informática.

Imagine-se uma diretora de colégio, responsável por preparar as classes para o próximo ano letivo. Como você é boazinha, decide deixar os alunos escolherem com quem eles querem ficar no próximo ano, então dá a possibilidade de eles escreverem em um papel nomes dos coleguinhas que mais querem encontrar no ano seguinte. Mas sendo uma diretora justa, você pergunta aos professores quais alunos seria melhor que não ficassem na mesma turma, uma “lista negra” de duplas que seria melhor que ficassem separados. Com essas duas informações: a preferência dos alunos e a lista negra dos professores, como determinar qual distribuição ideal de alunos?

Esse não é um problema fácil. Podemos pensar em tratar o problema brutalmente: listar todas as possibilidades e verificar qual satisfaz melhor às condições das listas, tanto a de preferência quanto a de exclusão, mas isso, com um número pequeno de alunos, logo atinge limites astronômicos. O número de configurações possíveis de sala será $2^{\text{numero de alunos}}$, com 100 alunos você teria algo perto de $10^{30}$ configurações. Meu processador i5 só aguenta algo perto de 10MIPS, o que me dá o direito de realizar $10^7$ instruções por segundo e eu precisaria de pelo menos $10^{23}$ segundos para fazer qualquer coisa com essas configurações, isso é mais que a idade do universo. Essa conta provavelmente está bem errada, mas acredito no argumento de que, para listar todos os casos possíveis, terei que investir mais que uma tarde em cálculos. Precisamos pensar em um jeito mais malandro.

Primeiro, vamos pensar no quadro teórico do problema e como implementar de maneira adequada. Eu quero um jeito prático de saber quantas condições uma configuração de alunos satisfaz e quantas ele viola. Vou atribuir pesos iguais à preferência dos alunos e à lista dos professores, poderiam ser diferentes, mas sou preguiçoso. Seja n o número de alunos. Tomo um vetor $S_n$ com $n$ coordenadas que podem valer 1 ou -1. Se $S_i=1$, então o aluno $i$ está na sala A. Se $S_i=-1$, o aluno $i$ está na sala B.

Em seguida, defino a matriz $J_{ij}$, que é $n\times n$. Ela contém a seguinte informação: $J_{ij} = 1$ se o aluno $i$ quer ficar com o aluno $j$. $J_{ij} = -1$ se não é legal que o aluno $i$ fique com o aluno $j$ e $J_{ij}=0$ se eles são indiferentes entre si. Eu poderia ter privilegiado a opinião dos professores atribuindo um peso muito negativo ao invés de -1, mas vamos dar uma chance as alunos e atribuir pesos iguais às preferências dos alunos e dos professores. Isso vai servir para calcular o quanto de “felicidade” a configuração gera. Se dois alunos estão na mesma sala e queriam estar na mesma sala, a felicidade aumenta. Se eles não podem estar na mesma sala e estão em salas separadas, a felicidade aumenta. Se estão em salas diferentes e queriam estar juntos, ela diminui. Mas como computar isso? Basta calcular: $J_{ij}\cdot S_i\cdot S_j$.

Se eles estão na mesma sala, o produto $ S_i\cdot S_j$ será 1 e, se querem estar na mesma sala, $J_{ij}$ será 1, então o resultado será 1. Se não podem e estão na mesma sala, o resultado será -1. Se não estão na mesma sala, o produto $S_i\cdot S_j$ é -1. Deu para entender que esse produto representa bem a “felicidade” gerada pelo estudo de um par de alunos. Precisamos, então somar $J_{ij}\cdot S_i\cdot S_j$ para todos os $i$’s e $ j$’s e isso dará a felicidade da configuração.

Mais uma vez, isso exige produtos e somas com $2^n$ configurações possíveis, é absolutamente impossível resolver esse problema na força bruta para mais de 50 alunos. Para tal, precisamos de um método mais eficiente, e eu escolho Monte Carlo.

O método de Monte Carlo é um dos mais poderosos e usados na física estatística para resolver esse tipo de problema impossível. Tomamos uma configuração inicial de classes aleatória (um vetor $S$ aleatório) e procedemos da seguinte forma:

  • Trocamos um aluno de sala (tiramos $i$ aleatório e fazemos $S_i\to -S_i$)
  • Checamos a felicidade da nova configuração.
  • Se aumentou, ele fica nessa sala nova.
  • Se diminuiu, ele volta para a primeira sala.

Você ficaria impressionado em saber que, com 50 alunos, eu consigo a configuração certa de $S$ em menos de 1000 iterações. Claro, tomei um $J$ agradável o suficiente para que eu soubesse qual a configuração certa e esse $J$ em particular provavelmente facilitou minha vida. Tomei a sala em panelinha: metade dela quer ficar entre si e não pode ficar com a outra metade. Eu esperava um S da forma $(1,1,\ldots ,1,-1,-1,\ldots ,-1)$, e o tenho rapidamente com esse algoritmo.

Sabendo um pouco mais de física, eu poderia te contar que os átomos possuem uma propriedade chamada spin, que pode apontar para cima (1) ou para baixo (-1). Em uma rede cristalina, os spins interagem e são capazes de definir muita coisa, como, por exemplo, se a rede será um imã ou não. O que acontece é que os spins sempre atingem uma configuração que minimiza a energia da rede, e essa energia é calculada se o material é antiferromagnético (os spins gostam de ficam em direções opostas) ou ferromagnético (eles preferem se alinhar). Em algumas redes, você até mistura esses dois tipos e calcular a magnetização total (o conjunto de todos os spins) pode parecer um inferno.

Mas a energia total é calculada da seguinte forma: você multiplica os spins para saber se estão alinhados ou não, se estão, o produto será positivo, se estão invertidos, o produto será negativo. E então você multiplica pelo fator $J_{ij}$, que vale 1 se o material é ferromagnético ou -1 se é antiferromagnético (ou 0 se os spins estão longe e não interagem). A energia total será a soma para todos os i’s e j’s de $J_{ij}\cdot S_i\cdot S_j$ onde $S_i$ é o spin da partícula $i$. A magnetização do sistema será a configuração de spins que minimiza essa energia. Ora, é difícil não ver que a magnetização de um material misto entre dia e ferromagnetismo é o exato mesmo problema que uma diretora de escola enfrenta ao escolher quais alunos ficarão em qual sala.

Esse método, Monte Carlo, parece quase milagroso, mas possui um problema grave. Não é o caso da matriz $J$ que escolhi, que é extremamente agradável, mas com algum outro $ J$ eu poderia ter um sério problema. Eu poderia atingir uma configuração em que trocar qualquer aluno de sala causaria uma queda na felicidade, mas que, se eu trocasse dois ou três, poderia ter um ganho. Esse tipo de situação é um “mínimo local” da felicidade, um defeito sério em Monte Carlo, que não pode escapar de um mínimo local e atingir a verdadeira configuração ideal de salas, pois ele só aceita ganhos reais e imediatos. Como podemos nos livrar disso? Ah, precisamos de uma adaptação de Monte Carlo, chamada “Algoritmo de Metrópolis”, mas isso fica para outro dia, a diretora da minha sétima série, pelo que escrevi, já terá bastante trabalho pela frente.

1 resposta

O segundo bissexto

Rookie

Os que nascem hoje envelhecem menos que os outros. Comemorando apenas aniversário uma vez a cada quatro anos, os nascidos no vinte e nove de fevereiro são agraciados com problemas em preencher formulários online o resto de suas vidas, mas são privilegiados, nasceram em um dia especial, resultado de a rotação da terra em torno do Sol possuir alguns quebrados depois do 365 dias.

Esses quebrados são corrigidos com esse dia, mas até os quebrados possuem quebrados e esse ajuste não é perfeito. Precisamos pular um ano bissexto a cada 100 anos, e o fazemos, mas nem esse ajuste é ideal; podemos pular apenas os anos bissextos múltiplos de 100 que não são múltiplos de 400 (o que explica o ano 2000 ter sido um bissexto tão especial, a exceção da exceção). Isso deixa as coisas mais acertadas, só começaremos a perceber os efeitos dos quebrados dos quebrados em muitos milênios.

Enquanto o 29 de fevereiro é bem famoso, seu equivalente menor, o segundo bissexto, ou segundo adicional, não é muito conhecido. Diversos anos no último século contaram com o segundo adicional, suas contagens de ano novo estavam quase sempre adiantadas. Os grandes relógios atômicos do mundo que regem a contagem padrão das horas na terra estão cientes desse fato, há um conselho que define quando um ano terá um segundo extra e, quando isso acontece, o relógio do dia 31 de dezembro ou 30 de junho mostra, durante um segundo, a marca 23:59:60 antes de ir ao 00:00:00. Se não acredita, veja este relógio atômico:

[youtube=http://www.youtube.com/watch?v=34wDgYEOUJU]

Enquanto é fácil entender o 29/02, ele resulta do fato de a rotação da Terra em torno do seu próprio eixo e sua rotação em torno do Sol não serem múltiplos perfeitos, o segundo bissexto é mais difícil. Nós definimos o segundo como bem entendemos, não poderíamos ter definido um segundo que coincide exatamente com um divisor inteiro do dia terrestre, e não precisar acrescentar segundos, já que o ano possuiria um número exato de segundos, sem quebrados? Poderíamos, e fizemos isso, no século XIX. Mas o dia, desde então, se tornou mais longo. Vamos entender a razão disso.

Você deve ter visto a Lua diversas vezes à noite. Quando eu era menor, eu e minha mãe conversávamos sobre o que víamos “desenhado” na Lua. Ela via um coelho, há quem veja São Jorge e um dragão, eu via um rosto triste. E em todas essas conversas, eu jamais havia reparado: eu via sempre a mesma coisa na Lua. Mas se a Terra gira, em torno de si e do Sol, como a Lua conspira para sempre ter a mesma face virada para nós?

The Dark Side of the Moon não é apenas um excelente album do Pink Floyd, é como é chamado o lado oculto da Lua. O nome engana, esse lado da Lua recebe a mesma quantidade de luz solar que o outro lado, mas nunca o vemos da Terra. O período de rotação da Lua em torno de si mesma é exatamente o mesmo de sua rotação em torno da Terra, por isso ela sempre aparece com o mesmo rosto em nossas noites. Isso acontece pelas chamadas forças de maré, a força gravitacional da Terra afeta a Lua de tal forma que, por mandar gases e líquidos de um lado para o outro, a rotação da Lua acabou desacelerando e atingindo uma configuração estável. Se a Lua está sempre com o mesmo lado virado para a Terra, não há mudanças entre “maré alta” e “maré baixa” nela, então a rotação não perde mais velocidade. Se perdesse mais, essa variação recomeçaria, essa configuração de “lado oculto” e “lado visível” é a mais estável que a Lua consegue encontrar.

Longe dos filmes B de ficção científica, a rotação da Terra está, aos poucos, perdendo velocidade pelo mesmo motivo da Lua: o Sol causa suas forças de maré e pouco a pouco nossa rotação diurna vai se ajustando à rotação anual. Em muitos bilhões de anos, a Terra terá essas rotações coincidentes, teremos um lado constantemente exposto ao Sol e outro oculto, dia perpétuo e noite perpétua.

A Lua gira em torno da Terra há menos tempo (ou ao menos o mesmo tempo) que a Terra gira em torno do Sol, mas esse “acoplamento de maré” aconteceu muito antes na Lua que na Terra porque a distância Terra-Lua é bem menor que a Terra-Sol e o tamanho da Lua é bem menor, as forças de maré surtem mais efeito nela. No século XIX, os físicos definiram o segundo. Agora, para compensar o ganho de 2 milissegundos (0,002 segundos) de nosso dia por século (sendo cada ano 365 dias, se cada um deles fica 2ms mais longo, isso equivale a um ano 0,73s mais longo), inserimos o segundo bissexto. O último ocorreu no Reveillon de 2008 e o próximo será dia 30 de junho deste ano.

Enquanto isso pode não parecer muito, é interessante notar que os dinossauros, tendo vivido há 180 milhões de anos, possuíam dias uma hora mais curtos, a rotação da Terra era mais rápida. Em muitos milhões de anos, teremos dias cada vez mais longos, nossos descendentes, se existirem, poderão dormir 12 horas e ainda trabalhar outras 16. Eu, decididamente, nasci na época errada.

1 resposta

O gás de Coulomb-Dyson

Hardcore

Esses dias trombei com um assunto bonito, uma parte do estudo de matrizes aleatórias que realmente achei interessante. Claro, trabalho com matrizes aleatórias, então é um pouco normal eu encontrar coisas bonitas aqui e ali, mas dificilmente algo tão bonito quanto o que achei outro dia em um desses livros de teoria espectral. Aviso, esse post é nível hardcore e provavelmente o mais intenso que já postei até agora, recomendo discrição. Se você não é um físico ou matemático, não vai pescar muita coisa do texto, não aconselho sua leitura.

As matrizes aleatórias servem para bastante coisa. Diversos modelos envolvendo um operador com perturbação aleatória e fora de nosso controle podem ser colocado em um formato de matriz aleatória, a transmissão de dados de um conjunto de antenas a outro com ruído pode ser modelizado por uma equação linear com uma matriz aleatória também, muita coisa entra nessa categoria e em cada um desses estudos a pergunta é recorrente: jogando entradas aleatórias em uma matriz, com uma densidade de probabilidade $ P(x)$ para as entradas, qual será a densidade de probabilidade de seus autovalores?

Porque, no fundo, é nisso que estamos interessados. Na quântica eles serão as medidas possíveis, nas equações diferenciais lineares eles nos darão a estabilidade do sistema, autovalores são a alma das matrizes. Mas se encontrar os autovalores de uma matriz $ n \times n$ bem definidas já não é tarefa tão fácil, resolver polinômios sempre dá preguiça, é difícil não sofrer só ao pensar como será com matrizes cuja única informação é a probabilidade de obter suas entradas entre dois valores.

Primeiro vamos estabelecer o que eu quero dizer com “probabilidade de uma matriz”. De forma civilizada, eu precisaria temperar esse texto com alguns detalhes da medida usada, do espaço em questão, mas isso é um blog e não um artigo; essa história está mais bem contada neste excelente artigo sobre matrizes aleatórias, ainda nas primeiras páginas. Tomemos um exemplo fácil, um vetor $ (x,y)$. Falar de sua densidade de probabilidade, é falar de uma função $ P(x,y)$ tal que, para descobrir a chance de encontrar esse vetor com as coordenadas $ 0\leq x \leq 3$ e $ 0 \leq y \leq 2$ será o resultado da integral $ \int_0^2 dy \int_0^3dx P(x,y)$, simples assim. Se $ x$ e $ y$ são independentes, certamente teremos $ P(x,y)=P(x)P(y)$, mas isso não será necessariamente verdade. Falar de densidade de probabilidade de uma matriz é falar da densidade conjunta de suas entradas, ou seja, sua j.p.d.f. (joint probability density function). Eu usaria o termo em português, mas não gosto de abreviar função densidade de probabilidade.

É claro que nem as matrizes nem as probabilidades podem ser quaisquer, problemas gerais demais não levam a lugar nenhum. Vou me restringir ao caso real, tudo pode ser generalizado para complexo com as devidas trocas. Listo dois tipos de matrizes cujo estudo das probabilidades é interessante: matrizes cujas probabilidades das entradas são independentes e matrizes que possuem a probabilidade invariante por conjugação.

Essa última propriedade é mais sutil, mas é simples. Dizer que a j.p.d.f. de uma matriz $ M$ é invariante por conjugação é dizer que, para toda $ U$ não singular, teremos que $ P(M)=P(UMU^{-1})=P(M’)$, ou seja, a chance de obter um elemento da classe de conjugação de $ M$ é a mesma chance de se obter $ M$.

E essa propriedade serve para uma manobra bem útil. Se a j.p.d.f. é invariante por conjugação, e se eu consigo diagonalizar a matriz, a probabilidade da matriz será a mesma probabilidade de sua forma diagonal, com seus autovalores como entradas, o que me permite de maneira fácil obter a distribuição de probabilidade de seus autovalores. Por vários motivos, físicos e matemáticos, gostamos de estudar matrizes simétricas, ou hermitianas se complexas. Isso vai garantir a diagonalização por matrizes unitárias e a existência de um alegre conjunto de autovalores bem reais.

Teorema: O único grupo de matrizes aleatórias invariantes por conjugação unitária e cujas entradas possuem p.d.f. independentes é o grupo das matrizes gaussianas, cujas entradas possuem como p.d.f. uma distribuição normal.

Nem arrisco tentar demonstrar isso, tomaria este post e mais outros três. Esse teorema nos inspira a aprofundar nosso estudo das matrizes gaussianas. Como elas são invariantes por conjugação unitária (estamos ainda com matrizes simétricas se reais e hermitianas se complexas, então elas são diagonalizáveis por uma matriz unitária), podemos escrever que $ P(M) = P(D)$, onde $ D$ é sua forma diagonalizada. Para que isso seja possível, vamos nos restringir às matrizes gaussianas simétricas (hermitianas se são complexas). Como em $ P(M)$ as probabilidades das entradas individuais são independentes, nosso instinto nos diz que em $ P(D)$ as coisas serão parecidas, que os autovalores terão probabilidades independentes, e não poderíamos estar mais errados. Porque escrever $ P(D)$ é escrever $ P(\lambda_1,\lambda_2,ldots,\lambda_n)$, uma probabilidade que depende dos autovalores, isso é uma mudança de variável e, como a probabilidade sempre se dá integrando essa densidade de probabilidade, precisamos levar em conta o jacobiano dessa transformação que, para nosso desespero, acopla todos os autovalores. Tal probabilidade já é conhecida há algum tempo, a j.p.d.f. dos autovalores da matriz gaussiana:

\[P(\lambda_1,ldots,\lambda_n) = C_k e^{-\beta \sum_k \lambda_k^2} \prod_{j<k}|\lambda_k-\lambda_j|^\beta \]

E o último termo da direita, a parte do jacobiano relativa aos autovalores, não é ninguém menos que o determinante de Vandemonde. O $ \beta$ é um valor referente ao tipo da matriz gaussiana, vale 1 se ela é real, 2 se é complexa e 4 se estamos nos quatérnions. E agora vem a parte bonita: Dyson (nisso fui corrigido, disseram ser Wigner, deixo a polêmica) percebeu que essa j.p.d.f. poderia ser colocada de uma forma mais familiar, bastava apenas jogarmos o determinante de Vandermonde para o expoente como $ \prod_{j<k}|\lambda_k-\lambda_j|^\beta = e^{\beta \sum_{j<k} \log |\lambda_k-\lambda_j|}$, teremos que a probabilidade será um múltiplo de uma grande exponencial. Chamar aquele número de $ \beta$ é extremamente sugestivo. Um leitor atento já deve ter percebido, contemplamos um peso de Boltzmann, em uma analogia perfeita a uma j.p.d.f. do sistema canônico:

\[P(\lambda_1,ldots,\lambda_n) = C_k e^{-\beta\left(\sum_k\lambda_k^2-sum_{j<k}\log |\lambda_k-\lambda_j|\right)} = \frac{1}{Z}e^{-\beta H}.\]

A magia dessa interpretação é poder importar todas as ferramentas da física estatística para resolver esse intrincado problema de álgebra linear. Se imaginarmos que cada autovalor representa a posição de um elétron confinado a uma linha (que representará o eixo real), atraídos ao centro por um potencial harmônico (o termo em $ \sum_k\lambda_k^2$ ) e submetidos à repulsão coulombiana mútua (que em sua forma bidimensional é $ \log |x_i-x_j|$), teremos um sistema físico cujas posições dos elétrons são equivalentes às posições dos autovalores da matriz gaussiana. E, caramba!, isso é muito bonito.

A analogia não é apenas formal, podemos extrair diversas propriedades dessa distribuição com técnicas do ensemble canônico (meu orientador, aliás, fez a carreira dele nisso). E este é um de meus exemplos favoritos de física ajudando matemática, ainda que, se fôssemos contar pontos nisso, a competição seria injusta, estaríamos perdendo por uma boa margem.

1 resposta