Quando eu era garoto, conheci um problema de lógica e desenho que deve ser famoso. Apresentaram-me a seguinte figura:
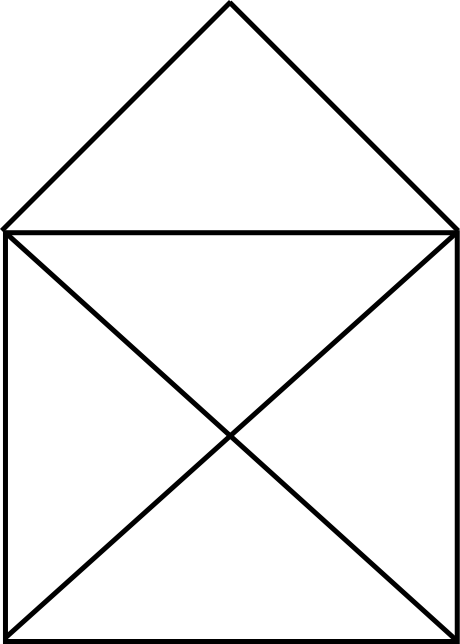Sendo o objetivo do problema desenhar essa figura sem tirar o lápis do papel e sem repetir os caminhos. Após algumas tentativas, cheguei a um caminho correto, desenhava feliz a casa com o X segundo as regras. Foi então que me foi apresentado uma variante do problema, “mais difícil” segundo aquele que me passou. Fui desafiado a desenhar essa outra figura:
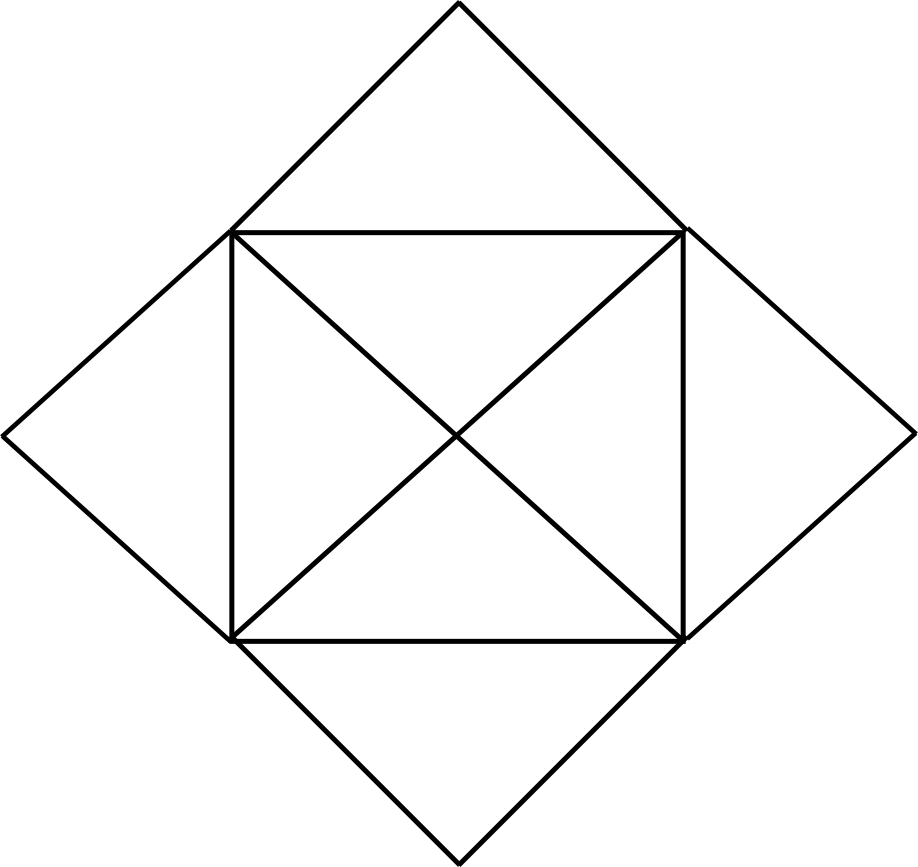Passei anos tentando, vez ou outra, resolver esse problema. Deixei de dar atenção a ele depois dos treze anos e, aos dezoito, descobri que todas aquelas tentativas fúteis de desenhar essa estranha flor foram justificadas: o problema não tem solução, é impossível encontrar um caminho que desenhe essa figura sem tirar o lápis do papel e sem repetir caminhos.
Mal sabia eu que esse mesmo problema, ou quase, havia sido resolvido por Leonhard Euler na cidade de Konigsberg, Prússia, em 1735. Euler garante com tranquilidade um lugar no top 3 da matemática, ostentando ainda hoje o título de matemático com maior número de publicações, tendo passado os dez últimos anos de sua vida cego (e publicando matemática, claro) e, segundo dizem, foi um excelente pai de seus cinco filhos. Ao passar pela cidade de Konigsberg na Prússia, Euler foi desafiado com um problema típico da cidade. Ela possuía duas ilhas no rio ligadas entre si e com a terra por sete pontes, como mostra a figura descaradamente roubada da Wikipédia:
E o desafio era atravessar as sete pontes sem repetir nenhuma. Você pode se divertir tentando, como os habitantes da cidade faziam, mas Euler decidiu pensar no problema de maneira mais profunda. A primeira coisa que fez foi se livrar do que estava sobrando: prédios, ilhas, estradas, apenas as pontes importavam:
Numerei as massas de terra para que a identificação com o desenho seguinte fique mais clara. Não contente, Euler percebeu que podia simplificar ainda mais o diagrama escrevendo-o da seguinte forma:
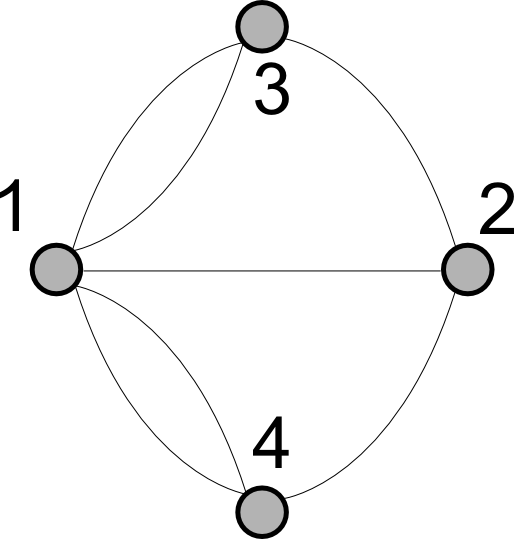A vantagem desse formato, minimalista ao extremo, é nos permitir focarmos apenas no que realmente importa. E esse foi o raciocínio de Euler: quero atravessar todas essas linhas sem jamais repetir nenhuma. Rapidamente, ele notou que, para não repetir linhas, todo ponto a que ele chegasse deveria permitir uma saída, exceto, claro, pelos pontos inicial e final. Ou seja, para todo o ponto, exceto os de começo e fim, cada entrada deve possuir uma saída correspondente: ele deve possuir um número par de conexões. Se ele possui um número ímpar, digamos, 3; eu entrarei nele, sairei dele e, na próxima entrada, não terei como sair, eu travei e, ao menos que ele seja meu ponto final, perdi o jogo.
Olhe agora o diagrama das pontes de Konigsberg. Todos os pontos possuem um número ímpar de linhas, quando o número máximo é dois (entrada e saída). Assim, Euler concluiu de uma vez por todas que não é possível atravessar as sete pontes de Konigsberg sem jamais repetir nenhuma.
E Euler também responde a meu problema da flor estranha. Enquanto a casa com o X possui todos os vértices com um número par de linhas exceto pelos dois na “base” da casa, eu consigo criar o caminho e desenhá-la sem repetir linhas. E mais: sei sempre que os pontos de começo e fim serão os da base, é impossível fazer o caminho sem começar por eles, são os únicos com um número ímpar de conexões. Quanto à flor, todos os vértices do quadrado central possuem cinco conexões, qualquer caminho leva ao fracasso e meu problema está resolvido.
Curiosamente, quando trabalhava na usina nuclear, um colega propôs-me esse problema da flor, alegando que seria interessante já que eu “gostava dessas coisas” e que ele não conseguia resolver. Vingando-me daquele que em minha infância apresentou-me o problema, disse triunfante ser impossível e, naquela mesma lousa, contei as linhas de cada vértice. Porque matemáticos não levam muito bem a ideia de “não conseguirem algo” e, não conseguindo, ao menos provam que ninguém no mundo consegue.
Então a conclusão é que não há formas de desenhar a flor sem repetir caminhos? A explicação foi bem clara mas não objetiva, o que acabou me confundindo.
Exato, é impossível desenhar a flor. Ela possui muitos vértices com um número ímpar de linhas, invariavelmente você acaba ficando preso em algum deles. Sinto a explicação não ter sido objetiva. 🙂
E como vc fez a da casinha??
Comece pelo pé direito dela, suba, faça o telhado, siga a diagonal de volta ao ponto de partida, siga para o outro pé à esquerda, suba, faça a parte de baixo do teto, siga a outra diagonal e você terá terminado. O segredo é sempre começar pelo pé da casa e terminar no outro pé.
qual nome da flor
Não sei, não vi tantas referências a esse problema além da vez que mo apresentaram quando eu tinha dez anos e, dez anos depois, em meu estágio em uma central nuclear.
sabe como se desenha um quadrado com x
Olá Ricardo, minha turma da escola recebeu 3 desafios na aula de filosofia, o envelope, um quadro de números e a MALDITA flor, consegui resolver a flor dobrando o papel e logo meu professor disse que estava errado, eu vejo em toda internet que é impossível, mas as pessoas que já resolveram dizem que é possível, estou extremamente frustrado tentando resolver há semanas.
Caro Leandro,
as pessoas que dizem que já resolveram estão mentindo. Um grafo, para ser ligado sem repetir e sem tirar o lápis do papel, precisa ter no máximo dois vértices com um número ímpar de entradas+saídas. Se houver dois, um será o de entrada e um de saída. Se houver mais de dois, você sempre fica preso em um deles. A menos que essas pessoas tenham usado algo que não está nas regras, como dobrar o papel, furar o papel ou alguma feitiçaria, é impossível. E não impossível do tipo “eu sou fraco e não consigo”, impossível do tipo “Jesus, durante sua segunda vinda, cheio de poder e majestade, não conseguiria se tentasse”. Se alguma pessoa conseguir, elas estará ou violando as regras, ou violando as leis da lógica.
Sinto em lhe informar, mas acabei de desafiar as leis da lógica!! Pois consegui, se quiser até mando um vídeo te mostrando.
Eu adoraria receber esse vídeo! Mas não vale usar aqueles shenanigans de furar o papel, dobrar a folha e tudo mais.
Ola, estou a meses tentando resolver esse digamos desafio, se vc recebeu este vídeo tem como me mandar? Fiquei muito curiosa
Como esperado, não recebi vídeo nenhum. Não é possível desenhar a “flor” usando as regras do jogo.
ola gostaria de sabe como resolvo um desafio,é uma casinha com um x no quadrado , porem ela tem um risco no triangulo , e esse risco é diagonal como faço pra resolver???
e toda vez que vou tentar fazer fica faltando um lado o que faço ??
A mais de 25 anos tinha este problema sem resolver, fico feliz em saber que é impossível. 🙂
Há muitos anos atrás, uma professora substituta de matemática pegou um livro e começou a desenhar este objeto aí na lousa, e falou que era para desenhar sem tirar o lápis do papel e sem repetir as linhas. E a aula toda foi só isso, uns bagunçando porque sabia que não valia nota e outros interessados tentando fazer. Eu era um dos interessados e fiquei tentando a aula toda. A professora disse que iria passar a resolução na aula seguinte, uns dias depois. Mas na aula seguinte, a professora oficial voltou a dar aula e nunca obtivemos a resolução que a substituta havia prometido. Depois disso, conseguimos perguntar para ela se ela tinha a resolução, e ela disse que não lembrava e que precisava olhar no livro (coisa que nunca fez e nem ia fazer). E pra falar a verdade, pelo nível das aulas dessa substituta, não é de se duvidar de que nem sabia do que se tratava, ela simplesmente encontrou algo para entreter os alunos enquanto ficava sentada sem fazer nada. Um amigo até falou que eu tava enganado, que o desenho que ela passou faltava uma aba nas laterais, que não tinha quatro abas. Mas eu me lembrava perfeitamente que era com quatro completo. Então terminei os estudos sem saber disso aí, sempre tentei fazer hora ou outra, mas como todos disseram, sempre falta uma ligação não importa como você comece. Hoje resolvi pesquisar e caí nesse site. Muito obrigado por ter postado esse texto esclarecedor. Abraços!
Poxa tem um muito difícil a anos nunca consegui ele é um quadrado com um X no meio mais uma meia Lua em cada lado do quadrado
Tbm n
TEnho 45 anos etento desenhar essa flor a naos e so agora descobri isso, ja tentei de toda forma, desisto, obrigada
Tem um desafio que é o desenho de uma casa em 2d com várias portas e a regra é passar em todas as portas sem repetir a passagem das portas . Eu estou a muito tempo tentando resolver queria que vc Ricardo olhasse. Se quiser te mando pois não achei seu e-mail. Estou achando estranho esse desafio.
Também tento descobrir a resposta para esse desafio a mais de 20 anos… creio que seja o mesmo… a planta de uma casa, com total de 16 portas (uma em cada canto), precisa passar em todas as portas sem repetir a passagem das portas e sem cruzar as linhas. Pena que não dá para desenhar aqui ou postar o desenho para todos tentarem.
Estranho eu achava q so eu tentava desenhar esta imagem sem passar por cima me da ate medo em saber que existe mais peaaos que tentao , cheguei a me sentir mal frustar em nao consegui mesmo sabendo que é impossivel eu tentava nas refras normais nao tem como , doubradura e fazer outra kinha foge das regras de sentido
Adoro… também fui apresentada à esses problemas na infância. Vou aplicar uma atividade dessas com meus alunos. Quem se interessar, só me mandar msn. Bjss