Estatística com poucos dados sempre dá calafrios. Uma das grandes ameaças a qualquer conclusão de um estudo é, tendo poucos dados, você pode confundir um efeito real com pura sorte. Não estou nem falando de fontes de viés mais graves, como uma pesquisa online que privilegia quem tem acesso a internet ou uma pesquisa boca de urna que privilegia pessoas dispostas a parar para conversar. Estou falando de pura sorte, ou, no caso do experimento estatístico, puro azar de ter estudado casos que justamente apresentam uma conclusão diferente daquela que o estudo deveria ter dado. Hoje vamos falar dessa sorte, e de um de meus métodos favoritos para tentar separar o que é efeito e o que é acaso fortuito.
Quando você tem muitos dados e seu método de escolha não tem nenhum viés, é mais difícil sofrer com os efeitos do azar. A exata quantidade de pessoas que você precisa para evitar isso tem a ver com o teorema do limite central, um conceito que vale um post próprio. A ideia é que se você seleciona elementos o suficiente da população, você claro tem chance de pegar anomalias que poderiam mexer em seus resultados, mas se seu método de seleção é bom você deve pegar anomalias que puxam o resultado para o outro lado também. As bizarrices de uns compensa as bizarrices de outros e você termina com um resultado médio confiável. Mais ou menos como quando uma multidão sai de um estádio. Você nunca sabe para onde uma pessoa vai, mas a massa humana se move de maneira previsível e você pode criar mecanismos de escoamento adaptados a essa situação confiando nesse princípio fundamental da estatística. Mas muitos dados não é nosso caso hoje, vamos ver o que dá para fazer tendo apenas catorze.
Tenho catorze plantas de tomate e dois fertilizantes: marca A e marca B. Quero saber qual dos fertilizantes é melhor. Divido minha horta em catorze pedaços. Vou fertilizar a terra, plantar e regar, tendo plantado a mesma quantidade de pés de tomate em cada pedaço de terra. Porque não sou besta e sei que plantar com fertilizante A de um lado e B de outro pode criar uma tendência, afinal, a fertilidade inerente da terra pode estar associada com a região da horta (por receber mais sol, por exemplo), eu tiro na sorte qual fertilizante vai em cada pedaço. Tirar na sorte é fácil, basta pegar catorze cartas de baralho, sete vermelhas e sete pretas, embaralhar bem e tirar uma para cada pedaço de terra.
Com minha horta plantada, colho os tomates, peso e comparo o quanto obtive em cada pedaço de terra.
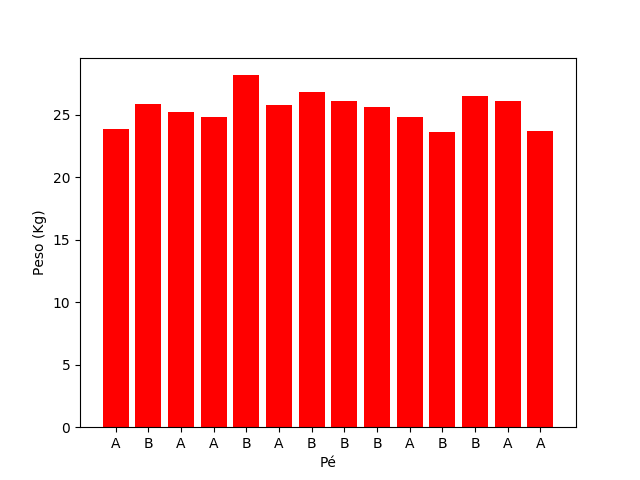 Não parece haver uma tendência de região. Digo, é possível, nunca se sabe se a tendência de região compensou a tendência do fertilizante, mas isso é um pouco especulativo. Temos nossos 14 resultados e queremos saber quem é melhor: A ou B. Fazemos a média do peso de tomates de cada um deles e o resultado é:
Não parece haver uma tendência de região. Digo, é possível, nunca se sabe se a tendência de região compensou a tendência do fertilizante, mas isso é um pouco especulativo. Temos nossos 14 resultados e queremos saber quem é melhor: A ou B. Fazemos a média do peso de tomates de cada um deles e o resultado é:
| Fertilizante | Média |
| A | 24.9Kg |
| B | 26.1Kg |
O B parece ser o vencedor, e um estudo qualquer talvez até pudesse parar aí: B é melhor. Mas prestando atenção com calma, ele não é tão maior assim, apenas 1.2Kg de diferença na média, sendo que os valores médios são vinte vezes maiores que essa diferença! É possível que a vantagem de B seja apenas sorte, um acaso surgido de uma experiência com poucos dados? Quão provável seria sair esse resultado se A e B fossem perfeitamente equivalentes?
Essa última pergunta é bem difícil de responder, porque não conhecemos a distribuição de probabilidade de A e B, ainda que fosse a mesma. Com bastantes dados, poderíamos estimar a distribuição, calcular desvio padrão, ter toda uma pletora de ferramentas e instrumentos estatísticos para nos ajudar, temos apenas catorze pontos e vamos nos virar com isso. Minhas estratégia será usar a aleatoriedade da nossa escolha de lugares para plantar para gerar “novos dados”, apostando na justiça do aleatório para decidir se essa diferença é significativa ou não.
Qual a ideia? Nossa escolha de lugares para plantar foi A, B, A, A, B, A, B, B, B, A, B, B, A, A; confiando no coração das cartas. A diferença entre as médias de A e B foi de 1.2Kg, então eu pergunto: se a ordem dos fertilizantes fosse trocada, com os resultados ficando onde estão, qual seria essa diferença. Por exemplo, se os sete piores resultados fossem do A e os sete melhores fossem do B, a diferença seria de 2Kg. Existem outras permutações da ordem dos fertilizantes que dariam diferenças menores, variando entre 0Kg e 2Kg. Estudando todas as configurações possíveis de fertilizante, guardando os resultados onde estão, ganhamos uma boa noção do quanto é sorte ou do quanto é efeito de verdade.
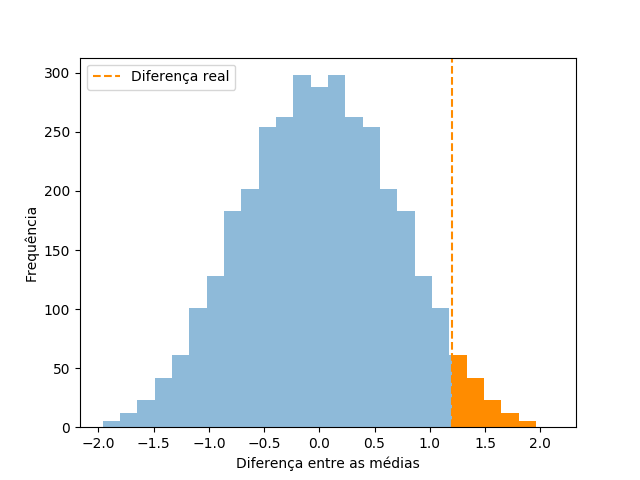
Temos 3432 permutações não-repetidas possíveis desse conjunto. Uma delas é A, B, A, A, B, A, B, B, B, A, B, B, A, A, cuja diferença entre as médias é de 1.2Kg. Como são as outras? O histograma abaixo dá uma boa ideia, onde os resultados são da diferença entre as médias de B e A (por isso pode ser negativo).
 Com apenas um resultado, quase invisível, no -2 e no 2, o resto todo distribuído simetricamente em torno de zero. A simetria é esperada, já que toda vez que existe uma permutação em que B ganha de A existe o oposto espelhado dessa combinação em que A ganha de B. E onde entra nosso caso, o caso real, nesse histograma?
Com apenas um resultado, quase invisível, no -2 e no 2, o resto todo distribuído simetricamente em torno de zero. A simetria é esperada, já que toda vez que existe uma permutação em que B ganha de A existe o oposto espelhado dessa combinação em que A ganha de B. E onde entra nosso caso, o caso real, nesse histograma?
Temos nosso resultado visualizado e com ele conseguimos ganhar alguma perspectiva. Basta contar quantas permutações de nosso conjunto produzem resultados maiores que a que obtivemos para estimarmos a probabilidade de termos dado sorte! Se nosso resultado estivesse muito perto do centro, muitas outras seriam mais discrepantes e a chance da diferença ter vindo do acaso fortuito passa a ser alta. Se nossa permutação fosse a que causa a maior diferença possível, teríamos quase certeza de que o tipo de fertilizante impacta profundamente a quantidade de tomates produzida por cada pé.
Em nosso caso, 133 das 3432 combinações possíveis são maiores que 1.2Kg, o que representa apenas 3.9% dos casos totais. Uma regra bem comum na estatística é estimar que se menos de 5% das permutações seriam melhores do que a realidade, então seu efeito provavelmente é real e não pode ser descartado facilmente. Não é uma regra fixa e perfeita, afinal, se o número de permutações fosse 6%, ou 7%, eu ainda poderia ficar desconfiado. Mas é uma maneira bonita, eu acho, de tirar leite de pedra, de fazer estatística com poucos dados sem perder o rigor da análise.
É um truque interessante que aprendi nas ruas, nem sempre temos todos os dados que queremos. É também útil para a vida, quando encontramos uma experiência na vida real e queremos estimar se um efeito é verdadeiro ou fruto do acaso. Se comparamos o horário de dois trens seis vezes e um deles está sempre mais atrasado que o outro, em todas as vezes, assumimos que o trem é atrasado porque a chance desse resultado acontecer com dois trens equivalentes é de $1/2^{6} \approx 1.6\%$. Usamos a medida do aleatório constantemente para dar chances a modelos que às vezes não merecem. É uma maneira fundamental de medir dois efeitos, usando o acaso como justiça, como o grande mediador do nosso experimento.