Esses dias trombei com um assunto bonito, uma parte do estudo de matrizes aleatórias que realmente achei interessante. Claro, trabalho com matrizes aleatórias, então é um pouco normal eu encontrar coisas bonitas aqui e ali, mas dificilmente algo tão bonito quanto o que achei outro dia em um desses livros de teoria espectral. Aviso, esse post é nível hardcore e provavelmente o mais intenso que já postei até agora, recomendo discrição. Se você não é um físico ou matemático, não vai pescar muita coisa do texto, não aconselho sua leitura.

As matrizes aleatórias servem para bastante coisa. Diversos modelos envolvendo um operador com perturbação aleatória e fora de nosso controle podem ser colocado em um formato de matriz aleatória, a transmissão de dados de um conjunto de antenas a outro com ruído pode ser modelizado por uma equação linear com uma matriz aleatória também, muita coisa entra nessa categoria e em cada um desses estudos a pergunta é recorrente: jogando entradas aleatórias em uma matriz, com uma densidade de probabilidade $ P(x)$ para as entradas, qual será a densidade de probabilidade de seus autovalores?

Porque, no fundo, é nisso que estamos interessados. Na quântica eles serão as medidas possíveis, nas equações diferenciais lineares eles nos darão a estabilidade do sistema, autovalores são a alma das matrizes. Mas se encontrar os autovalores de uma matriz $ n \times n$ bem definidas já não é tarefa tão fácil, resolver polinômios sempre dá preguiça, é difícil não sofrer só ao pensar como será com matrizes cuja única informação é a probabilidade de obter suas entradas entre dois valores.

Primeiro vamos estabelecer o que eu quero dizer com “probabilidade de uma matriz”. De forma civilizada, eu precisaria temperar esse texto com alguns detalhes da medida usada, do espaço em questão, mas isso é um blog e não um artigo; essa história está mais bem contada neste excelente artigo sobre matrizes aleatórias, ainda nas primeiras páginas. Tomemos um exemplo fácil, um vetor $ (x,y)$. Falar de sua densidade de probabilidade, é falar de uma função $ P(x,y)$ tal que, para descobrir a chance de encontrar esse vetor com as coordenadas $ 0\leq x \leq 3$ e $ 0 \leq y \leq 2$ será o resultado da integral $ \int_0^2 dy \int_0^3dx P(x,y)$, simples assim. Se $ x$ e $ y$ são independentes, certamente teremos $ P(x,y)=P(x)P(y)$, mas isso não será necessariamente verdade. Falar de densidade de probabilidade de uma matriz é falar da densidade conjunta de suas entradas, ou seja, sua j.p.d.f. (joint probability density function). Eu usaria o termo em português, mas não gosto de abreviar função densidade de probabilidade.

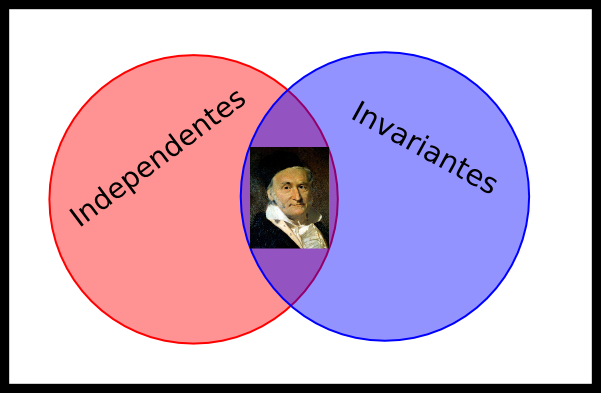
É claro que nem as matrizes nem as probabilidades podem ser quaisquer, problemas gerais demais não levam a lugar nenhum. Vou me restringir ao caso real, tudo pode ser generalizado para complexo com as devidas trocas. Listo dois tipos de matrizes cujo estudo das probabilidades é interessante: matrizes cujas probabilidades das entradas são independentes e matrizes que possuem a probabilidade invariante por conjugação.

Essa última propriedade é mais sutil, mas é simples. Dizer que a j.p.d.f. de uma matriz $ M$ é invariante por conjugação é dizer que, para toda $ U$ não singular, teremos que $ P(M)=P(UMU^{-1})=P(M’)$, ou seja, a chance de obter um elemento da classe de conjugação de $ M$ é a mesma chance de se obter $ M$.

E essa propriedade serve para uma manobra bem útil. Se a j.p.d.f. é invariante por conjugação, e se eu consigo diagonalizar a matriz, a probabilidade da matriz será a mesma probabilidade de sua forma diagonal, com seus autovalores como entradas, o que me permite de maneira fácil obter a distribuição de probabilidade de seus autovalores. Por vários motivos, físicos e matemáticos, gostamos de estudar matrizes simétricas, ou hermitianas se complexas. Isso vai garantir a diagonalização por matrizes unitárias e a existência de um alegre conjunto de autovalores bem reais.

Teorema: O único grupo de matrizes aleatórias invariantes por conjugação unitária e cujas entradas possuem p.d.f. independentes é o grupo das matrizes gaussianas, cujas entradas possuem como p.d.f. uma distribuição normal.

Nem arrisco tentar demonstrar isso, tomaria este post e mais outros três. Esse teorema nos inspira a aprofundar nosso estudo das matrizes gaussianas. Como elas são invariantes por conjugação unitária (estamos ainda com matrizes simétricas se reais e hermitianas se complexas, então elas são diagonalizáveis por uma matriz unitária), podemos escrever que $ P(M) = P(D)$, onde $ D$ é sua forma diagonalizada. Para que isso seja possível, vamos nos restringir às matrizes gaussianas simétricas (hermitianas se são complexas). Como em $ P(M)$ as probabilidades das entradas individuais são independentes, nosso instinto nos diz que em $ P(D)$ as coisas serão parecidas, que os autovalores terão probabilidades independentes, e não poderíamos estar mais errados. Porque escrever $ P(D)$ é escrever $ P(\lambda_1,\lambda_2,ldots,\lambda_n)$, uma probabilidade que depende dos autovalores, isso é uma mudança de variável e, como a probabilidade sempre se dá integrando essa densidade de probabilidade, precisamos levar em conta o jacobiano dessa transformação que, para nosso desespero, acopla todos os autovalores. Tal probabilidade já é conhecida há algum tempo, a j.p.d.f. dos autovalores da matriz gaussiana:

\[P(\lambda_1,ldots,\lambda_n) = C_k e^{-\beta \sum_k \lambda_k^2} \prod_{j<k}|\lambda_k-\lambda_j|^\beta \]

E o último termo da direita, a parte do jacobiano relativa aos autovalores, não é ninguém menos que o determinante de Vandemonde. O $ \beta$ é um valor referente ao tipo da matriz gaussiana, vale 1 se ela é real, 2 se é complexa e 4 se estamos nos quatérnions. E agora vem a parte bonita: Dyson (nisso fui corrigido, disseram ser Wigner, deixo a polêmica) percebeu que essa j.p.d.f. poderia ser colocada de uma forma mais familiar, bastava apenas jogarmos o determinante de Vandermonde para o expoente como $ \prod_{j<k}|\lambda_k-\lambda_j|^\beta = e^{\beta \sum_{j<k} \log |\lambda_k-\lambda_j|}$, teremos que a probabilidade será um múltiplo de uma grande exponencial. Chamar aquele número de $ \beta$ é extremamente sugestivo. Um leitor atento já deve ter percebido, contemplamos um peso de Boltzmann, em uma analogia perfeita a uma j.p.d.f. do sistema canônico:

\[P(\lambda_1,ldots,\lambda_n) = C_k e^{-\beta\left(\sum_k\lambda_k^2-sum_{j<k}\log |\lambda_k-\lambda_j|\right)} = \frac{1}{Z}e^{-\beta H}.\]

A magia dessa interpretação é poder importar todas as ferramentas da física estatística para resolver esse intrincado problema de álgebra linear. Se imaginarmos que cada autovalor representa a posição de um elétron confinado a uma linha (que representará o eixo real), atraídos ao centro por um potencial harmônico (o termo em $ \sum_k\lambda_k^2$ ) e submetidos à repulsão coulombiana mútua (que em sua forma bidimensional é $ \log |x_i-x_j|$), teremos um sistema físico cujas posições dos elétrons são equivalentes às posições dos autovalores da matriz gaussiana. E, caramba!, isso é muito bonito.

A analogia não é apenas formal, podemos extrair diversas propriedades dessa distribuição com técnicas do ensemble canônico (meu orientador, aliás, fez a carreira dele nisso). E este é um de meus exemplos favoritos de física ajudando matemática, ainda que, se fôssemos contar pontos nisso, a competição seria injusta, estaríamos perdendo por uma boa margem.