Arquivo mensais:outubro 2013

Correlações e matrizes I

Rookie

Muitos pediram para que eu dedicasse um post à técnica que usei no estudo de correlação dos votos dos políticos nos últimos posts. Gostei das análises e confio em minhas conclusões, mas isso aqui é ciência, meus métodos precisam estar claros para que eu ganhe credibilidade. Pretendo ainda explorar a montanha de dados que tenho das votações dos deputados, mas, como meu computador foi furtado e com ele foram os scripts de análise que tinha feito, mando um post intermediário sobre a técnica antes de continuar com mais resultados. Este post será um pouco árido, mas peço paciência, o assunto é fascinante e as aplicações são imensas em todas as áreas da ciência ou da análise de dados. Seguindo este roteiro, você pode encontrar correlações entre quaisquer duas variáveis em sua pesquisa, em sua empresa, em sua sala de aula.

Vou começar tratando um problema diferente, na área da pedagogia. Eu tenho as notas de física e matemática de dez alunos: Alice, Bruno, Carolina, Daphny, Eduardo, Frederico, Gabriela, Hugo, Igor e Jonas, que serão referidos apenas por sua letra inicial:

Aluno: A B C D E F G H I J
Fís 5,0 8,0 10,0 2,0 4,5 9,0 6,0 3,0 9,0 8,0
Mat 6,0 7,0 9,5 0,0 4,5 7,0 4,5 2,5 8,0 8,0

Quando eu me pergunto se há alguma correlação entre física e matemática, quero saber, sabendo a nota de um aluno em física, se consigo dar um bom chute de qual será sua nota de matemática. Essa tabela não ajuda muito, melhor seria se eu visualizasse meus alunos como os pontos em um gráfico:

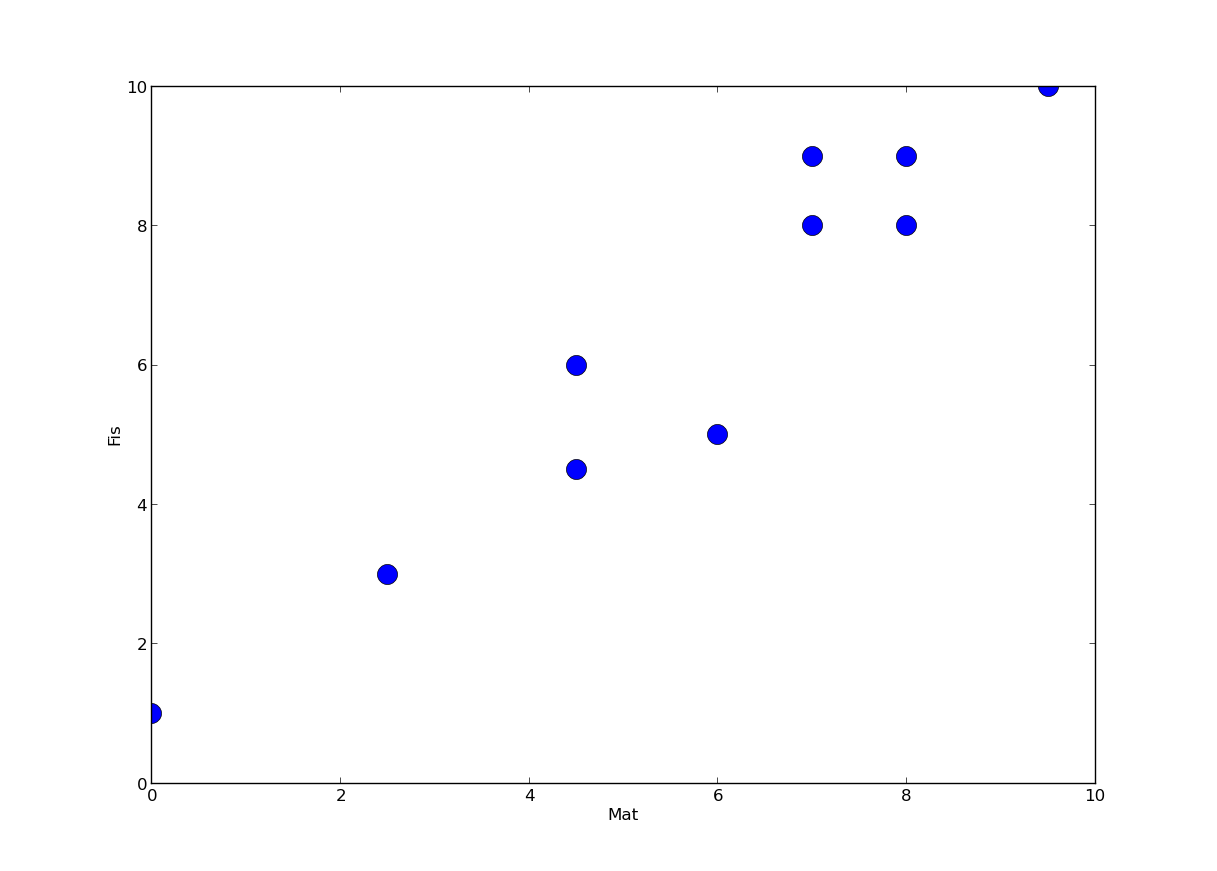correlacao_1Com o gráfico é mais fácil ver que parece haver uma forte correlação positiva entre física e matemática. Se um aluno é bom em matemática, esses pontos me dizem que é um bom chute dizer que ele também é bom em física. Como queremos um método decente de dizer isso, medimos a chamada correlação entre duas matérias. Há diversas maneiras de definir correlação, sendo a correlação de Pearson o exemplo mais clássico de medida de correlação. Intuitivamente, queremos que essa correlação seja alta quando as notas de física e matemática andam juntas, que seja perto de zero se as variáveis parecem independentes e que seja muito negativa se ter nota em física parece atrapalhar a nota em matemática.

Precisamos matematizar isso de uma maneira coerente. Quando um aluno tirar nota baixa nas duas matérias, quero que a correlação entre as matérias aumente, e também quero que ela aumente quando um aluno tirar nota alta nas duas. A correlação deve diminuir quando um aluno tirar nota alta em uma e baixa em outra. Mas qual seria a melhor definição de alta ou baixa? Por justiça e senso comum, uso a média da sala como parâmetro, e defino nota alta e baixa como acima ou abaixo da média. Para que as coisas fiquem bem claras, eu subtraio a média de cada nota e terei o novo gráfico:

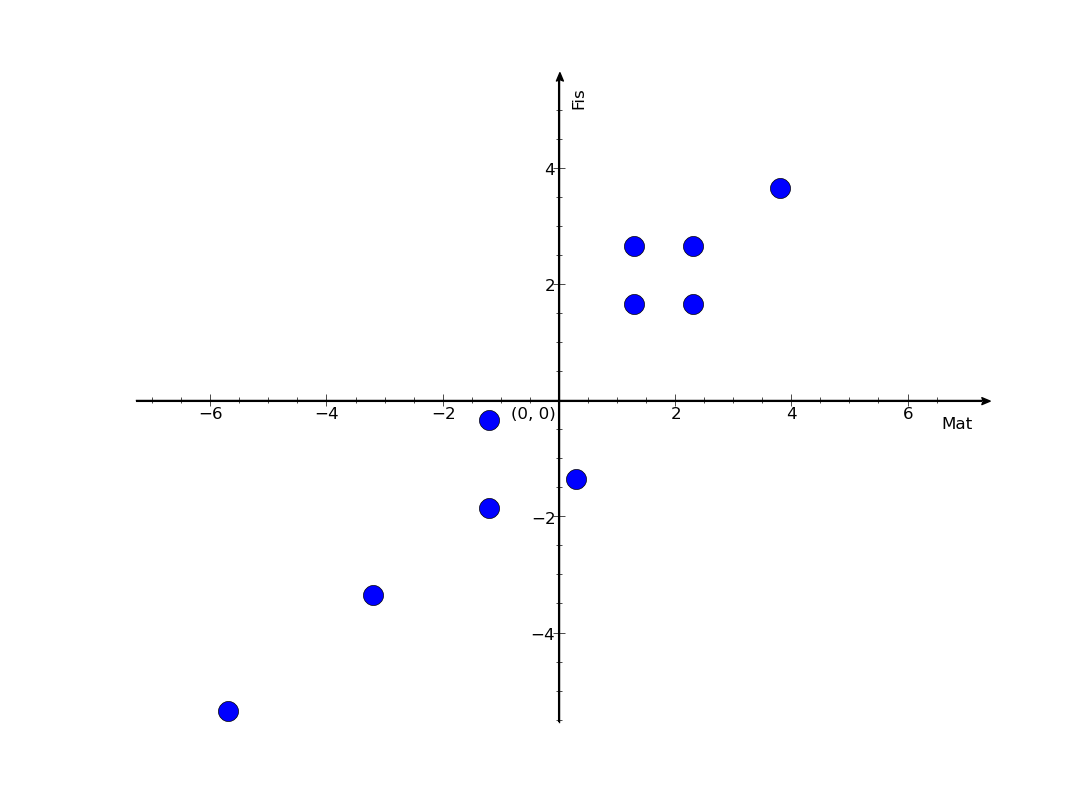correlacao_2E aqui já percebemos que a correlação entre essas matérias certamente é positiva. Notamos que pontos nos quadrantes 1 e 3 (positivo-positivo e negativo-negativo) são pontos que contribuem com a correlação entre as matérias, enquanto pontos nos quadrantes 2 e 4 diminuem essa correlação. Como tenho apenas um ponto no quarto quadrante, e ele está quase na fronteira, é fácil admitir que a correlação é positiva entre as matérias. Contudo, ver não é o suficiente, quero um número para essa correlação.

O que a correlação de Pearson diz é que cada aluno contribuirá com a correlação com um valor de acordo com o produto de suas notas. Essa noção é boa, pois menos vezes menos dá mais, então pontos nos quadrantes um e três contribuirão para aumentar a correlação e pontos nos quadrantes dois e quatro diminuirão esse valor. É importante notar também que, nessa métrica, pontos mais distantes da média contribuem mais com a correlação que pontos próximos. Isso é razoável, pois um ponto próximo da média nas duas matérias poderia estar em qualquer quadrante com pouco esforço, enquanto trazer o ponto D, o mais extremo à esquerda, a outro quadrante exigiria muita aula particular.

Antes de calcular esse valor, precisamos sanar outro problema. Se esse estudo fosse feito na França, as notas iriam de 0 a 20, pois usar base 10 nesse país é démodé. Esses dados teriam uma flutuação maior e as correlações calculadas seriam diferentes, ainda que a proporção entre eles fosse a mesma. Ainda que eu subtraia a média, os valores deixariam de flutuar entre -6 e 6 para flutuarem entre -12 e 12, o que tornaria multiplicações entre eles maiores e a correlação maior. Se a distância em relação à média de algum aluno fosse 5 em matemática e 4,5 em física, a contribuição na correlação seria 22,5 no Brasil; na França, seria quatro-vintes e dez! Não é porque eu mudo a escala que a correlação aumenta, uma análise da correlação de altura e peso da população não pode depender do uso de centímetros ou polegadas ((Contudo, estudar em polegadas é moralmente errado.)) .

O ideal seria dividir os valores por algo que leve em conta a dispersão deles, e um excelente candidato é o chamado desvio padrão. Essa grandeza nada mais é que a raiz da média dos quadrados dos elementos. Se as notas de física são 3, 5, 8 e 10, eu primeiro subtraio de todos a média, que é  6,5, tendo como notas -3,5, -1,5, 1,5 e 3,5. O desvio padrão será

\[\sqrt{\frac{(-3,5)^2+(-1,5)^2+1,5^2+3,5^2}{4}}=2.89.\]

Uma interpretação possível do desvio padrão é o quão longe da média os dados estão. Em nosso caso, parece bem razoável dizer que os dados estão a uma distância de 2.89 da média; mas note que ele coincidir com os valores mais distantes é uma coincidência do exemplo. Esse desvio padrão das notas, que denotaremos por $\sigma_F$ e $\sigma_M$ para física e matemática, é a quantidade que queremos para deixar as notas comparáveis. Assim, a correlação entre duas matérias é calculada somando o produto de cada par de notas e dividindo pelos desvios-padrão de cada matéria, ou seja:

\[\text{Corr }=\frac{F_1M_1+F_2M_2+\cdots+F_{10}M_{10}}{\sigma_F\sigma_M},\]

onde $F_1$ é a nota de física de um aluno e $M_1$ é sua nota de matemática. É importante notar que nessa definição a correlação máxima entre dois pontos é 1 e a mínima é -1, o que nos permite comparar correlações de objetos completamente diferentes usando a mesma escala. Isso é resultado da subtração da média e divisão pelo desvio-padrão, ferramentas que nos permitem equiparar grandezas completamente diferentes e analisá-las com o mesmo termômetro e mesma régua.

Calculando finalmente a correlação entre física e matemática, encontramos o valor 0,94. Ele é, como esperado, extremamente alto, já que o valor máximo é 1, o que mostra que notas de física e matemática, entre nossos alunos, estão profundamente correlacionadas. Em um chute ingênuo, mas honesto, com esses dados, é possível dizer que alunos bons em uma matéria são bons em outra, enquanto os que não sabem matemática também não parecem saber física.

Isso é esperado, porque, como o gráfico mostra, as notas estão praticamente alinhadas. Com esse método, temos um número, uma medida, para dizer o quão alinhadas elas estão. Notas perfeitamente alinhadas nos dariam correlação 1.

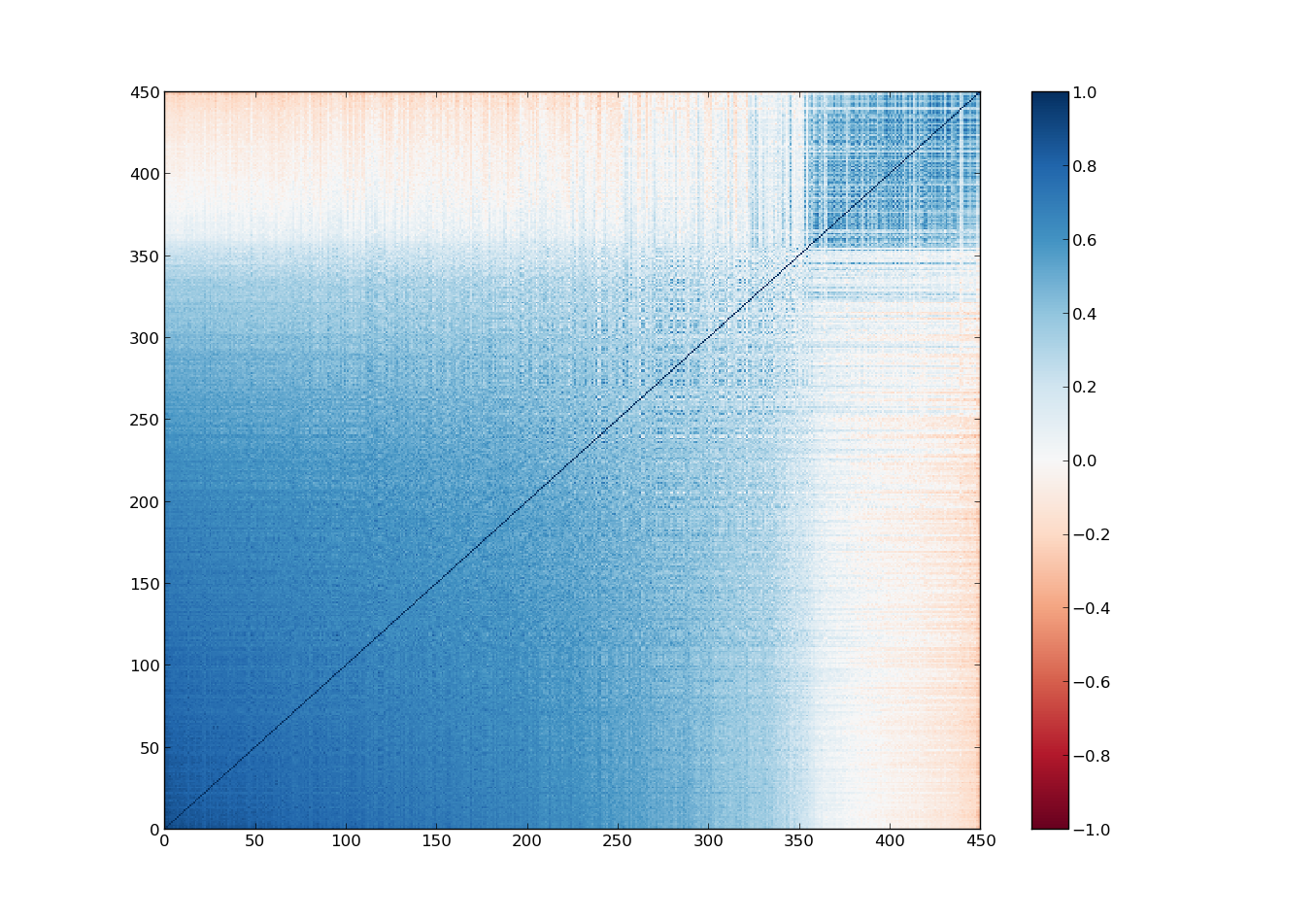
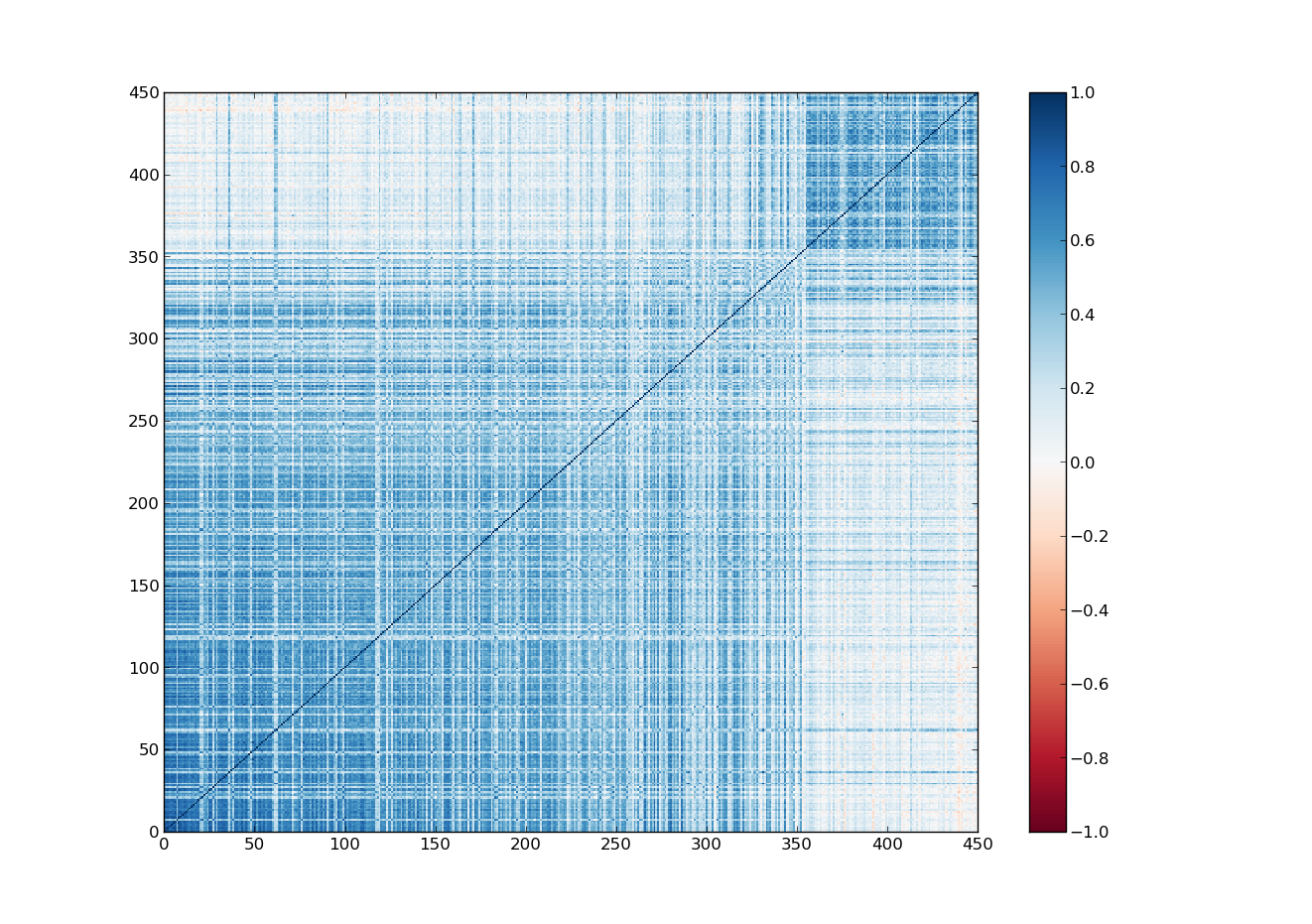
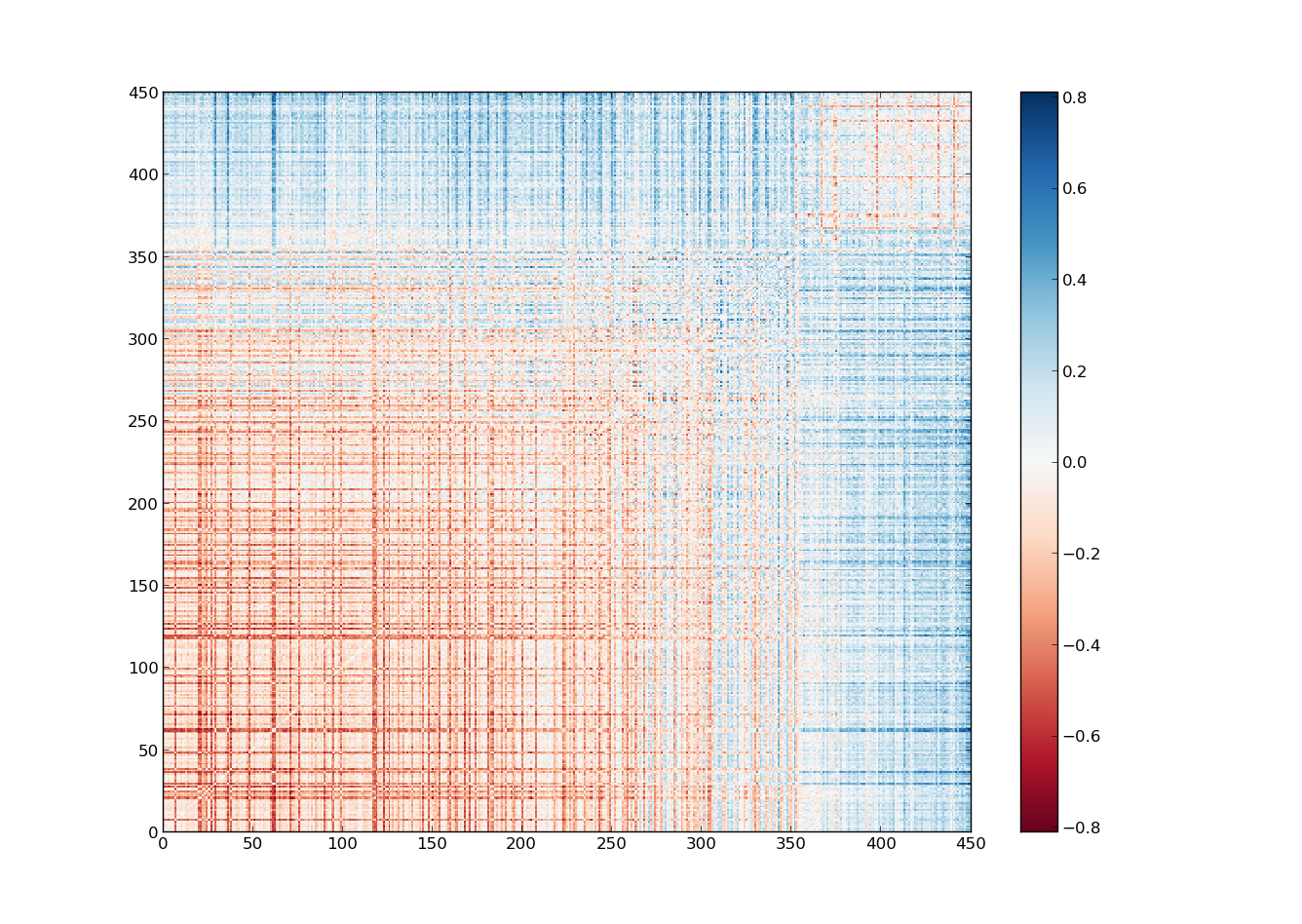
Atravessei todas essas definições com carinho para que fique claro o que é aquela matriz colorida dos deputados e senadores. Cada elemento é a correlação entre dois deputados, eles são o equivalente às matérias no meu exemplo. As notas dos alunos, no caso dos deputados, são as decisões que eles tomaram em uma votação, sendo 1 para SIM, -1 para NÃO e 0 para abstenção. A matriz funciona como um jogo de batalha naval, o senador da linha $i$ terá uma correlação com o senador da coluna $j$ representada pelo número no quadrado $(i,j)$ da matriz, sendo esses números de -1 a 1.

Claro que em outras circunstâncias eu teria mais cuidado para dizer que 0,94 é uma correlação grande, pois uma objeção razoável a esse tratamento todo é: quão grande é grande? A partir de 0,8? 0,7? Ainda que em um estudo menos formal você possa tomar o critério que mais lhe pareça razoável, como, por exemplo, dizer que 0,8 é o limite, é intelectualmente mais honesto comparar mais grandezas (em nosso caso, mais matérias) e afirmar que matemática e física, por exemplo, possuem mais correlação que matemática e português, se no caso as notas de matemática e português possuírem uma menor correlação.

No próximo post disserto um pouco sobre como ordenei a matriz e sobre como essa ordenação revela a estrutura de blocos e nos traz informações que, na frieza das tabelas, não são evidentes. Todo esse processo que descrevi pode ser automatizado com tranquilidade em qualquer software de tratamento de planilhas, cujo principal expoente é o Microsoft Excel. Tenho certeza de que na área de funções estatísticas há uma que calcula a correlação de Pierson de duas grandezas, mas entender de onde ela ver e o que ela significa é muito mais importante que calcular 0,94.

7 respostas

A força de uma narrativa

Rookie

Em meu último post, apresentei a vocês algumas técnicas estatísticas interessantes aplicadas ao estudo de correlações entre os partidos brasileiros. O assunto agradou, e muitos pediram um estudo parecido com a câmara dos deputados, com sua base amostral muito maior, seu jogo político mais acirrado, seria um estudo interessante em vários níveis. No entanto, não queria repetir exatamente o que fiz com os senadores, não queria mais do mesmo. Decidi, por isso, avançar em um assunto mais polêmico, e estudar a força de uma narrativa da política brasileira.

Lanço novamente o alerta: esse não é um blog político. Não tenho agenda partidária e minha opinião política é irrelevante na estatística. Tentei tratar os dados da maneira mais imparcial que pude, aceito sugestões dos que acharem alguma soma ou divisão injusta nessas linhas. A escolha do assunto é um interesse pessoal que partilho com muitos brasileiros: o escândalo na política apelidado mensalão.

A narrativa da acusação, resumidamente, é a de que durante os anos 2003-2004 a base aliada pagou uma espécie de mesada a deputados para fortalecer suas votações e assegurar o apoio da câmara aos projetos do governo. Base aliada e governo negam, sustentando sua inocência até o julgamento, que ainda corre. O escândalo explodiu no primeiro semestre de 2005, o que nos permite uma tentativa de análise nisso.

Tendo em mãos os votos dos deputados federais durante o primeiro mandato do governo Lula, pude dividir esses quatro anos em duas duplas: 03-04 e 05-06. Podemos nos perguntar como as correlações entre os partidos evoluíram entre esses dois biênios, pois, se a narrativa da acusação faz sentido, então a correlação entre governo e centro nos dois primeiros anos deve ser mais forte que nos anos seguintes, pois na primeira dupla o mensalão supostamente existiu, e foi desmantelado no início dos dois anos seguintes.

Claro, isso é uma simplificação grosseira, e proponentes de ambos os lados da narrativa podem interpretar os resultados da análise como quiserem. Se eu não encontrasse correlações, os mensalistas poderiam alegar que tal pagamento pode ter continuado no biênio seguinte. Eu encontrando correlação, os anti-mensalistas poderiam dizer que as mentiras vomitadas pelo partido da imprensa golpista fizeram o centro recuar do governo, ou que a mudança nas correlações é um resultado normal de uma crise política. A estatística é uma, mas a interpretação é sua.

Dito isso, vamos aos dados. Depois da publicação do último post, recebi uma chuva de dados, planilhas e banco de dados, e mando todos os meus agradecimentos aos que indicaram referências e especialmente aos do radar parlamentar pelo lindo banco de dados com todos os votos dos deputadores federais desde 1999. Infelizmente esse banco de dados não é meu, qualquer interessado pode entrar em contato com o grupo do radar e eles provavelmente ficarão felizes em compartilhar os dados. Aquele arquivo .xml foi um presente de natal, eu nem sabia o que fazer com tantos dados, senti-me uma criança presa na fábrica da Nestlé.

Para realizar a análise, tomei algumas decisões. Não podia considerar todos os deputados, alguns não possuíam relevância estatística suficiente. Excluí da análise qualquer deputado que tenha votado em menos de 10% das votações em qualquer um desses dois períodos. Ao todo, foram tomadas 259 decisões em 03-04 e 164 decisões em 05-06. A câmara possui 513 deputados, mas com este filtro apenas 450 sobreviveram para a análise. Os excluídos fazem parte dos que se tornaram prefeitos em 2005 ou daqueles cuja frequência no plenário deixou a desejar.

Primeiro, vejamos a composição da câmara no biênio 03-04, em uma matriz similar à usada no estudo dos senadores:

lula_1

Matriz de correlação da câmara nos anos 03-04.

Aos que não viram o último post, explico a matriz. Na linha $i$ e coluna $j$ você encontra a correlação entre o deputado $i$ e o deputado $j$ durante os anos 03-04. Se essa correlação é positiva, eles votam juntos. Se é negativa, costumam divergir. O tamanho da correlação será a coerência entre os votos desses deputados, muito alta, eles votam de forma praticamente igual, muito negativa, eles parecem querer votar um o oposto do outro. Essa matriz pode ser lida em blocos. Notando a existência de dois blocos, percebemos a existência de duas orientações políticas na câmara, que equivalem ao que chamamos de governo e oposição. Como no caso dos senadores, elas existem e são bem definidas. Além disso, há pouquíssimas regiões de anticorrelação, o que mostra que a câmara em 2003 buscou bastante o consenso; a própria natureza dos votos da câmara parece chamar mais concordância e unanimidade.

O segundo passo foi criar essa exata mesma matriz para o período 05-06, mas precisamos tomar cuidado. Devemos continuar com a mesma ordem da matriz, e essa ordem foi definida pelas correlações no primeiro período. Mantendo os mesmos deputados nas mesmas linhas, eu construo a matriz do segundo biênio do primeiro governo Lula:

lula_2_dep_1

Matriz de correlação da câmara nos anos 05-06.

Essa matriz está bem mais confusa, mas é o esperado, pois usamos a ordenação no período anterior, e certamente coisas mudaram entre os dois períodos. Ainda não conseguimos ver claramente o que mudou, ou o quanto mudou, por isso precisamos de um critério mais visual e preciso para medir a diferença, e uma subtração costuma ser bem eficaz para esse trabalho.

A matriz seguinte será a diferença entre as correlação de cada deputado comparando o período 05-06 ao período 03-04. Os exatos mesmos deputados são analisados. As regiões vermelhas, negativas, são aquelas que perderam correlação, ou seja, enfraqueceram politicamente de 03-04 a 05-06. As regiões azuis ganharam correlação, foram fortalecidas quando comparamos os dois biênios.

lula_delta

Diferença entre as matrizes de correlação do primeiro e segundo biênio do primeiro governo Lula.

E aqui temos um prato cheio para análise. A base governista perdeu muita correlação a partir do ano 2005, e, com isso, muita força política. Notamos que as mesmas pessoas que abandonaram o barco do governo, as “raias vermelhas” no bloco governista, concordaram substancialmente mais com o bloco da oposição. Essas raias que rasgam o espectro mostram um movimento massivo de políticos que votaram majoritariamente a favor do governo nos primeiros dois anos e trocaram de opinião, passando a contrariar a situação em um número relevante de vezes nos dois anos seguintes. Cada raia vermelha representa um deputado que em 2003-2004 votou diversas vezes a favor do governo e em 2005-2006 não apresentou o mesmo nível de concordância com a base da situação. O número de raias vermelhas no governo passa de 100.

É verdade que há raias vermelhas na oposição também, não podemos ignorá-las. Mas podemos contá-las, são cinco deputados que votavam com a oposição e passaram à situação, um número insignificante perto do fenômeno inverso, podendo ser explicado por flutuações estatísticas convencionais ou outras manobras políticas naturais ao congresso. Ademais, dentro da oposição há de tudo, aumento e perda de correlação, enquanto a base aliada é um mar de vermelho, não há nenhum ganho de correlação em todo núcleo da base aliada.

Em um próximo post, prometo a análise desses dados com os partidos em mente. Não exponho agora para não carregar em informação, e para não trair meu propósito inicial: avaliar a força de uma narrativa. A acusação do mensalão não cita (que eu tenha visto, correções são bem-vindas) partidos explicitamente, mas um fenômeno interpartidário em larga escala, dinheiro dado a parlamentares como persuasão a votarem de acordo com a situação. Olhando esta matriz, sou obrigado a concluir que a narrativa da acusação, que afirma a existência de um mensalão, é coerente com a estatística apresentada e explica os dados de maneira completa. Contando a partir da explosão do escândalo do mensalão, primeiro semestre de 2005, a correlação da base aliada ao governou caiu de maneira significativa e diversos deputados que estavam no núcleo da coerência governista votaram de maneira drasticamente diferente no segundo período do governo Lula.

Termino o post reiterando o aviso inicial: essa estatística não prova nada. Muitas explicações podem ser levantadas para essa mudança, os dois lados da história podem interpretar os dados como quiserem ou puderem, e podem levantar falhas na metodologia que tentarei responder ou consertar. Vou deixar esse ponto muito claro, porque não quero gente dizendo “Estatístico prova que mensalão aconteceu!”, correlação não implica causalidade. A única conclusão que posso tirar disso é a frase em negrito acima: a narrativa da acusação faz sentido. Se ela fosse verdade, esperar-se-ia dos votos dos deputados uma mudança cujo caráter é muito similar ao observado na realidade. Essa matriz não é prova, no máximo evidência, cuja interpretação e discussão deixo a quem entende do assunto.

19 respostas