Uma das leis físicas mais mal citadas, em diversos contextos e por ser um pouco difícil de explicar, é a segunda lei da termodinâmica: a lei responsável por prever que, ao colocar sua panela no fogo, não é o fogo que esquenta e ela que esfria; mas o contrário. Ela tem uma formulação complicada, a definição de entropia, de desordem e de reversibilidade, não vou me meter nisso hoje. Uma consequência dela, no entanto, é a seguinte propriedade: um sistema em equilíbrio térmico (todo mundo à mesma temperatura) precisa gastar energia para criar uma diferença de temperatura, ou seja, um lado quente e um frio. E essa propriedade é bem evidente, não por menos sua geladeira é ligada na tomada: ela usa essa energia para criar um ambiente frio (o interior do refrigerador) e um quente (aquela parte atrás que você usa para secar roupas e não devia).
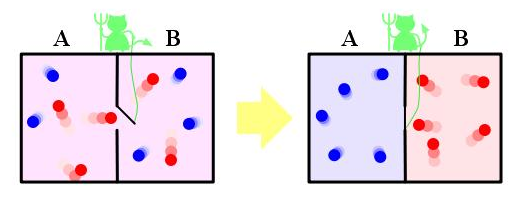
Quando esse princípio foi formulado, no meio do século XIX, foi um dos pais da termodinâmica, o gigante na física James C. Maxwell, o primeiro a elaborar uma tortuosa ideia em busca de uma melhor compreensão da lei. Um bom jeito de entender uma lei da física é tentar imaginar um sistema que a viola, e foi o que ele fez. Imagine uma caixa com um gás, dividida em dois compartimentos (esquerda e direita) separados por uma parede. Essa parede, contudo, possui uma pequena porta, e essa porta é controlada por um pequeno demônio que possui informações sobre cada partícula na caixa. Cada vez que uma partícula rápida do lado esquerdo se aproxima da porta, o demônio a deixa passar para o direito; e cada vez que uma partícula lenta no lado direito se aproxima da porta, o demônio a deixa passar para o lado esquerdo. Essa figura ajuda, tirada do site phys.com.
Como temperatura não é nada mais que a medida da agitação média das partículas, esse demônio acaba de separar o gás em um lado quente e um lado frio. Se essa porta for leve o suficiente, ou uma porta rolante de atrito zero, o trabalho de abrir a porta é nulo e o demônio, sem gastar energia, criou uma diferença de temperatura. Sem precisar ligar na tomada, o demônio criou uma geladeira. Essa ideia, que de fato é um pouco absurda, ainda assim tenta provar um ponto: alguém com bastante informação sobre o sistema pode violar a segunda lei da termodinâmica.
Gostamos de nossas leis, não queremos que elas sejam violadas tão facilmente. O demônio de Maxwell assombrou físicos por quase um século, demoramos para perceber onde estava a energia gasta pelo demônio para dividir o gás em quente e frio. Enquanto muitos tentaram atacar a parede no problema, ou a própria natureza irreal da situação, a resposta estava no cérebro do demônio.
Maxwell foi muito malandro na escolha de palavras, pois o problema logo no início tenta te enganar: ele usa um demônio, uma criatura imaterial, para fazer o serviço. Ele sabe tudo, ou ao menos sabe o que se passa em torno da porta, e decide abrir ou não a porta com essa informação. Mas precisamos imaginar que, se ele sabe, essa informação está armazenada em algum lugar. Surpreendentemente, a energia gasta pelo demônio de Maxwell está no fato de sobre-escrever a informação que possuía sobre a partícula levando em conta o fato de ter aberto a porta e tê-la deixado passar.
Essa resposta parece um pouco roubada, mas foi uma das grandes descobertas do meio do século XX, o nascimento da teoria da informação. Quando os computadores começaram a surgir, muita gente se colocou a tentar estabelecer os limites de cálculo de uma máquina daquelas, e quanta energia ela gastaria para realizar operações. No início, acreditava-se que toda operação feita pelo computador possuía uma energia mínima para ser realizada, o valor $k_BT\log 2$, onde $k_B$ é a constante de Boltzmann e $T$ é a temperatura. Esse limite, proposto por von Neumann, não está correto, mas quase. Se estivesse correto, seria impossível criar computadores funcionais, a quantidade de energia necessária para fazê-los rodar seria alta demais e resfriá-los seria quase impossível. Apenas em 1961 Laudauer explicaria o limite corretamente: apenas uma operação do computador precisa de gasto de energia: a operação de apagar uma memória.
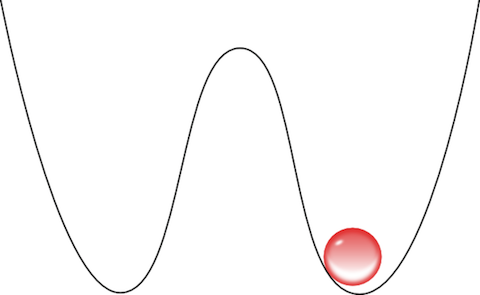
O argumento de Laudauer é simples e bonito. Vamos pensar na forma mais simples de se armazenar uma informação: o bit. Essa variável vale 0 ou 1, e deve ser armazenada de alguma forma, seja uma alavanca para um lado e não para outro, seja um aparato que permite ou não passar corrente. De forma bem geral, representamos o bit da seguinte forma:
Essa figura é um potencial, que podemos deformar à vontade, mantendo uma pequena bolinha de um lado e não do outro, representando o bit 1, enquanto no lado esquerdo seria o 0. Vamos supor que a temperatura da bolinha seja baixa o suficiente para que a chance de mudar de lado nesse potencial seja desprezível, como uma colina alta demais para que a bolinha vermelha, na velocidade em que está, possa atravessar e chegar ao outro lado.
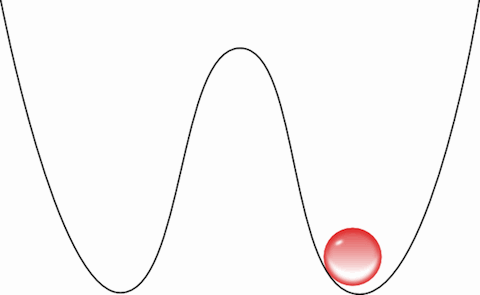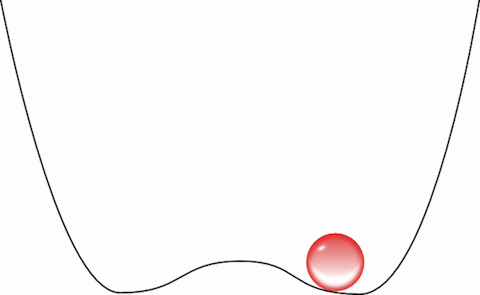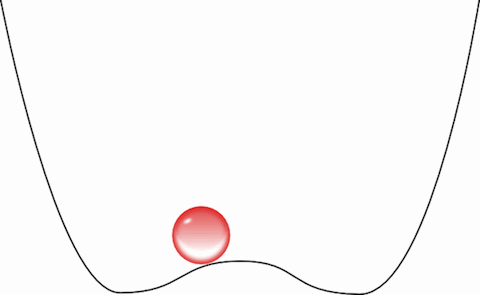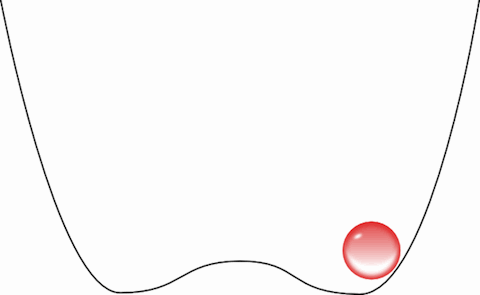
Queremos operar esse bit, transformá-lo de 1 em 0, ou seja, fazer a bolinha passar da direita para a esquerda. Esse processo é o equivalente a sobre-escrever uma informação: devemos primeiro esquecer o que havia e depois forçar a bolinha a ficar do lado que queremos. A primeira coisa que precisamos fazer, portanto, é descer a barreira e “apagar” a informação:
Agora a bolinha passeia livremente entre os dois bits. Esse gif não é muito honesto, a bolinha, para ser coerente com a física, precisa ir e voltar muitas vezes, esse processo de descer a barreira deve ser feito de forma quasi-estacionária, ou seja, devemos descer a barreira levando um tempo muito maior que o tempo característico da bolinha de ir de um lado para o outro. Assim, a bolinha faria o caminho de ida e voltas muitas vezes antes de ver a barreira descer. Logo mais discutiremos se isso é realmente possível.
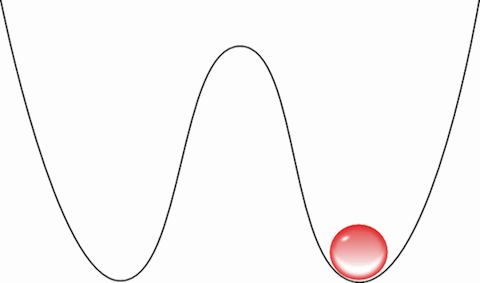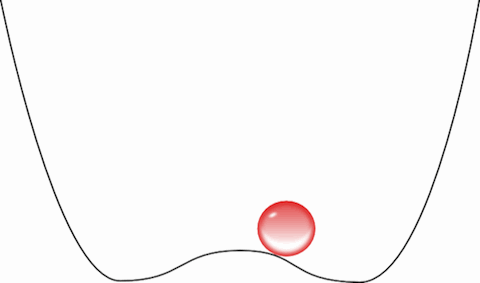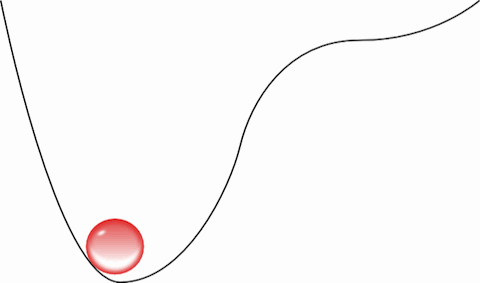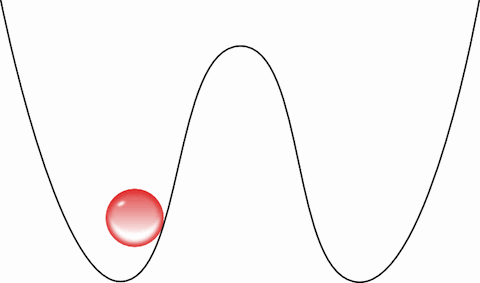
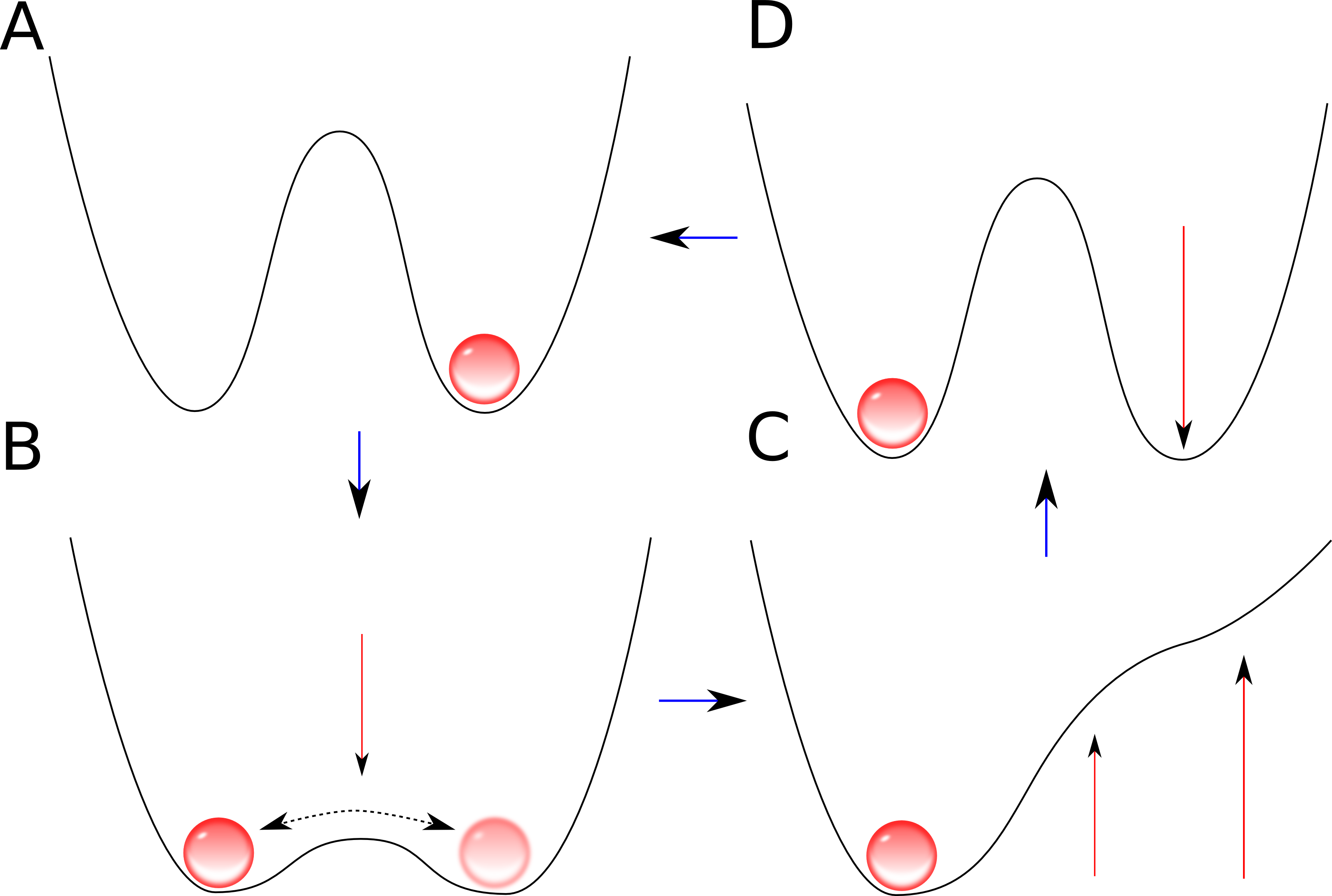
O próximo passo, escrever a informação, consiste em levantar a barreira de potencial de forma a forçar pouco a pouco a bolinha a ir para o lado que queremos. Enquanto ela vai e vem, vamos aumentando a barreira da direita. Isso forçará a bolinha a ficar confinada na esquerda. Em seguida, descemos a barreira da direita e temos a bolinha confinada do lado que queremos. O processo todo é resumido no seguinte gif, feito com algum esforço e uma tarde livre:
Vamos conversar agora sobre cada etapa desse processo, e as energias envolvidas. Queremos saber se precisamos gastar energia para sobre-escrever a memória e, se precisamos, em qual etapa exatamente. Para tal, vamos dar nomes às etapas:
Para entender o que está acontecendo, precisamos de algumas noções de termodinânica. Dizemos que um processo é reversível quando não há aumento de entropia, o caminho inverso pode acontecer. É importante notar que todo processo reversível deve ser quasi-estacionário: é necessário que cada ponto desse processo seja um estado de equilíbrio, o equivalente a dizer, de maneira grosseira, que não podemos mexer o sistema muito rapidamente se temos a pretensão de seguir o caminho inverso. A ideia é mover um pouco, bem pouco, esperar o equilíbrio chegar, mover mais um pouquinho, esperar o equilíbrio chegar, e continuar dessa maneira. Em uma situação idealizada, podemos dizer que as mudanças são infinitesimais e que o processo, a cada instante, está em equilíbrio.
Note que esse raciocínio não é de todo desonesto, pois estamos buscando o limite mínimo de gasto de energia. Na busca do limite, trabalhamos com a situação mais idealizada possível, e concluímos que melhor que isso não conseguiremos jamais.
Assim, as etapas são realizadas em um processo quasi-estacionário, de forma a estar constantemente no estado de equilíbrio. Queremos um pouco mais que quasi-estacionário, queremos fazer todas essas etapas em processos reversíveis. Se conseguíssemos, como não aplicamos nenhum trabalho na bolinha (ela não ganhou energia nenhuma, não mudou sua altura máxima atingida no poço), não teremos gasto energia nenhuma e teremos trocado a bolinha de poço. É então que Landauer nos diz: isso não é possível. Para ser mais exato, todos os processos podem ser feitos sem gastar energia, exceto passar de A para B.
Apagar uma memória é a única operação que gasta energia. Nosso raciocínio do “quasi-estacionário” não se aplica ao processo AB, e é por isso que nossa ideia falha. Quando dizemos “um processo lento”, queremos dizer lento em relação ao tempo que o estado leva para estar em equilíbrio. Mas conforme vamos descendo o poço, notamos que, se o poço é muito alto, o tempo característico para que a bolinha mude de poço é muito alto. Ora, na situação A o tempo que a bolinha leva para mudar de poço é infinito, e na situação B ele é finito, é, portanto, impossível realizar o processo AB de forma quasi-estacionária, porque você, em algum momento, terá o tempo característico de mudança de poço igual ao tempo característico de descer o poço. Em outras palavras, é impossível realizar um processo mais lento que um processo cujo tempo característico para atingir o equilíbrio é infinito!
Todos os outros processos, se feitos de forma bem devagar, podem ser realizados de forma completamente reversível. O que pega é o processo de apagar a memória, de deixar o bit indeciso, e é aí que o demônio perde. Em seu cérebro, ou em seu supercomputador, ele deve, a cada vez que deixa uma partícula passar, reescrever sua informação sobre a trajetória da partícula, porque, pela vontade dele, ela mudou de lugar e não será mais a mesma. O demônio gasta energia, uma forma de “energia mental”, para reajustar seu conhecimento à nova configuração.
Isso resolve o problema do demônio de Maxwell, que deve gastar energia para criar essa geladeira microscópica. Por mais conhecimento que tenha, ele deve apagar e sobre-escrever bits no momento em que decide que a partícula mudará de lado. Para o demônio, nessas condições, o maior esforço não é lembrar, analisar ou mudar a partícula; seu maior esforço é, de forma quase poética, esquecê-la.


Pingback: Férias | Todas as configurações possíveis
Excelente, faltam ensaios sobre física como esse na nossa língua, ainda mais online. Explicação perfeita.
Adorei o post, mas fiquei com uma dúvida: não sobra uma certa definição circular nessa demonstração? Apagar um bit me parece um mini experimento do demônio de Maxwell: é necessário saber a velocidade e a posição da particula no poço.
Eu pensei que pudesse sobrar algum conflito com o princípio da incerteza tb, mas fazendo a caixa arbitrariamente grande isso passa a não ser um problema.
Outra coisa, não é possível argumentar simplesmente que a porta da caixa não pode ser aberta de forma reversível pelas razões citadas? (se o processo AB é irreversível e demanda energia, porque abrir a porta pode não demandar energia?)
Além de muito interessante, isso parece dar dicas pra outros limites significativos: apagar um bit rapidamente deve requerir cada vez mais energia; fazer caixas menores deve requerir mais tempo para manter tudo quase-estacionário — e por conseguinte, tanto a miniaturização quanto a rapidez das memórias deve requerir mais energia!
Abraço
Para apagar um bit eu preciso apenas descer a barreira de potencial, não preciso de informação nenhuma sobre a bolinha. Descendo a barreira quando a bolinha está exatamente sobre o potencial faz com que a partícula acabe efetuando trabalho para mim, e nisso ela perde energia. O problema está no fato de que, como não tenho como saber posição e velocidades a ponto de prever completamente a partícula, nisso age o princípio da incerteza se estamos em escalas atômicas, eu não tenho como descer esse potencial sem gerar esse trabalho por acidente. Não sei se ficou mais claro, espero ter ajudado.
Sim, agora ficou mais claro, acho que estou quase entendendo 🙂 ! Esse trabalho fornecido pela partícula é perdido pois esse processo não é reversível, isso está certo?
Mas a outra dúvida que persiste: abrir a porta da caixa de Maxwell não seria igualmente irreversível? A resposta parece ser que neste caso sabemos as velocidades das partículas e portanto a chance da energia perdida não existe, seria isso?
Última pergunta: esse argumento não fica meio circular também no sentido de que o que dita que o processo é irreversível parte da segunda lei, que está em questão?
Ou seja não temos algo como
Hip: 2a lei -> gasto energia pra apagar bit -> demonio de maxwell falha -> 2a lei
Hip: Nao 2a lei -> sem gasto de energia pra apagar bit -> demonio de maxwell tem sucesso -> Nao 2a lei
O que nâo prova nada sobre a 2a lei?
Proponho uma objeção: O que acontece quando a barreira de potencial desloca-se perpendicularmente ao sentido da força que a partícula pode aplicar-lhe (como uma porta de trilho?
Proponho algo mais: Considere um êmbolo com uma divisória móvel a que se prende um fio ideal que passa por um orifício ideal para permitir apenas a passagem do fio. Digamos que o bit consista no lado do êmbolo onde há gás (ou uma partícula apenas). Acrescente-se também a essa barreira móvel a capacidade de abrir-se permitindo a passagem livre de gás (além da capacida de se mover ao longo do comprimento do êmbolo.
A proposta consiste no seguinte procedimento de esquecimento: a barreira é destravada de sua posição central original de tal modo a ser movida pelo trabalho do gás de um de seus lados, o qual é transmitido para o fio ideal. Uma vez completo o movimento, a barreira é aberta, mas sem que nenhum gás a atravesse (porque ela já estava em uma das extremidades). Em seguida, a barreira é posicionada novamente no centro sem que para isso seja necessária a aplicação de trabalho, uma vez que a barreira está aberta. Fecha-se então a barreira.
O resultado é que estamos na posição de esquecimento. Para posicioarmo-nos novamente em alguma posição de conhecimento, bastaria abrir a barreira (e não ocorreria aí nenhuma perda de informação, porque a informação já estaria perdida), posicioná-la na extremidade oposta ao lado onde querermos confinar a(s) partícula(s), fechar a barreira, e reconduzí-la em regime quase estático ao centro, mantendo-a, então, fechada.
Que lhe parece?