Aprendemos ainda no ensino primário sobre o método científico, e eu até lembro dessa aula. A professora trazia um ovo para a classe e pedia hipóteses sobre o destino do ovo ao ser jogado ao chão. Enumerávamos da mais óbvia à mais absurda, e por fim a professora abandonava o ovo e ele tocava o solo, estava completamente cozido e não fazia sujeira, para entendermos que o método científico é: observação de um problema, formulação de hipóteses, experimento controlado e conclusões.
Tornei-me cientista, pesquiso física, e ganho muitas caras de interrogação quando anuncio a alguém minha profissão. Cientista parece mais profissão de filme, um homem louco em jaleco cercado de vidros coloridos e de poucos amigos. Quando admitem que sou cientista, a próxima pergunta sempre é: “mas o que você faz, exatamente?”. E, para essa pergunta, e para dar uma versão mais real do método científico, listei alguns acontecimentos de um dia meu de trabalho e relato hoje com vocês. Nomeei-o “O método científico”, mas talvez título mais próprio seria “A Day in Life”. Esse post terá alguns detalhes científicos do que faço, é normal alguém de fora da área não os compreender, vou tentar explicar conforme escrevo.
9h30 Chego ao trabalho. Cheguei cedo, não costumo estar aqui antes das 10h, então aproveito para tirar de minha cadeira as coisas que o russo com que divido sala deixou ontem, escrever algo no blog, responder emails, preparar uma caneca de Earl Grey.
10h30 Passei uma hora fazendo o que deveria tomar quinze minutos, é a vida. Abro o Mathematica (programa que costuma fazer contas para mim, mas na realidade é minha cota de autoflagelação semanal). E eis meu problema de hoje: inverter uma transformada de Laplace (o que consiste a uma operação matemática bem difícil). Tento lembrar de minhas aulas sobre essa transformada, a razão de estar usando ela, tudo parece vago e um pouco difícil, vou só mandar o Mathematica fazer: InverseLaplaceTransform[f[s],s,t].
10h45 Mathematica está há quinze minutos na mesma conta, sem me devolver nada, é hora de aceitar a derrota e tentar achar um jeito mais inteligente de fazer isso.
12h Depois de alguma procrastinação com os colegas de laboratório que foram chegando, e depois de ter me forçado a manipular um pouco a forma exata da inversa transformada de Laplace, abandono qualquer esperança de resolver o problema exatamente. A forma exata é bem feia, chama-se integral de Bromwich, e não parece ser um bom caminho. Existem outros métodos, a fórmula de inversão de Post, mas tudo parece fadado ao fracasso, pois a função que quero inverter é, em um caso simples:
\[(100^{-6 – i – j} \Gamma[6 + i + j] \Gamma[-6 – i – j + s] \text{Hypergeometric1F1}[6 + i + j, 7 + i + j – s, 1/100])/ \Gamma[s] + 100^{-s} \Gamma[6 + i + j – s] \text{Hypergeometric1F1}[s, -5 – i – j + s, 1/100].\]
Vou abandonar e tentar fazer isso numericamente.
14h30 Voltei do almoço e parti para o Google buscando métodos numéricos de inversão de Laplace. Descobri como instalar coisas no Mathematica, isso é bem útil. Achei um método bom, chamado Piessens, e ele parece funcionar para funções cuja inversa da transformada eu já conheço (como $\frac{1}{s^2}$).
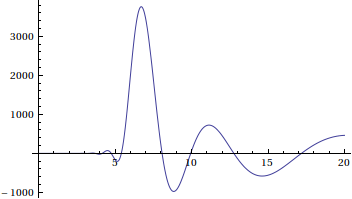
15h Eis o resultado do Piessens:
O que seria um resultado animador, se o que eu estivesse procurando não fosse uma probabilidade, e ainda não inventaram probabilidade negativa. Há algo errado ou com minha função, ou com o Piessens. Desço e compro um chocolate, preparo outro Earl Grey.
16h Minha função parece boa, o problema é no Piessens, e isso está me deixando nervoso. Durante minha palestra de exposição desse problema, um colega russo (não aquele com que divido sala) perguntou se não valia a pena abrir a série em Taylor e inverter termo a termo, eu respondi que não podia garantir a convergência, mas agora essa ideia parece animadora, tendo em vista a probabilidade negativa.
16h45 Maldito russo, aposto que ele nunca tentou abrir em Taylor e mandar a transformada. Sabe quem é a inversa de Laplace de $x^n$? A n-ésima derivada da delta de Dirac. Agora imagine eu com uma bela coleção de derivadas do delta com coeficientes diferentes para somar, de quê isso me serve? Era para ser uma probabilidade! Veio uma ideia: integrar essa probabilidade para ter a cumulada. Sabe o que acontece? A probabilidade de obter um valor menor que $r$ não depende de $r$ ! E a razão fica evidente uma vez que o método fracassa, só pode ser culpa da inversão da soma com uma operação integral, que pode ser resolvida com o teorema:
Teorema (da convergência dominada de Lebesgue): Ninguém troca integral com limite impunemente.
Vou tentar baixar outro método.
17h15 Achei um, chamado GWR, funciona para funções simples.
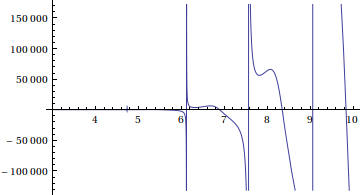
18h Eis o resultado com GWR:
E, depois desse gráfico, surge aquele pensamento de “o que estou fazendo com minha vida…?” aliado a uma vontade desenfreada de arremessar o Mathematica pela janela.
18h30 Depressão, seguida de raiva, dá lugar à aceitação. Fim de jogo, vou para casa, amanhã penso em outra coisa. Tento a barganha, ao menos, em um único dia, descobri três maneiras diferentes de não resolver meu problema.