Hoje é meu aniversário, celebro vinte e quatro anos de vida. E essa data, além de me fazer sentir especial, costuma me lembrar de um problema fascinante de combinatória, que levou a um igualmente interessante estudo econômico. Como não achei referência ao estudo, nem lembro onde o li, repeti-o eu mesmo, na medida do possível. O problema é conhecido como paradoxo do aniversário, que de paradoxal não tem nada.
A pergunta é: quantas pessoas eu preciso colocar em uma sala para que a chance de haver naquela sala pessoas com o aniversário repetido seja maior que a chance de não haver pessoas com o aniversário repetido? Formulado de outra maneira, eu tenho $N$ pessoas em uma sala e uma probabilidade $P(N)$ de que essas pessoas possuam aniversário repetidos, qual o primeiro valor de $N$ para o qual $P(N)>0,5$?
E a resposta é um número surpreendentemente baixo: 23. A partir desse valor de pessoas, é mais provável encontrar pessoas com aniversários repetidos que não encontrar, a probabilidade de que duas pessoas tenham nascido no mesmo dia do ano passa a 50,7% para esse valor de $N$. A razão do número ser pequeno é o grande crescimento da função fatorial, usada para calcular o número de combinações possíveis para a comparação de cada par de pessoas. Ou seja, apesar de haver muitos dias no ano, o número de comparações possíveis entre o aniversário de 23 pessoas é suficientemente grande para tornar essa probabilidade maior que 50%.
Interessados nesse resultado, podemos testar os aniversários de partidas de futebol. Sendo 11 para cada lado e o juiz, teremos 23 pessoas a cada partida, e podemos comparar um número grande de partidas para perceber que há mais partidas com aniversários repetidos que partidas sem aniversários repetidos.
No entanto, o resultado não será o que esperamos. De fato, há muitas partidas com aniversários repetidos, mas um número muito maior que o esperado! As partidas com aniversários repetidos ocorrem em número muito maior que as que não possuem aniversários em comum, quando a diferença não deveria estar muito longe de 51% contra 49%. Esse fato foi-me apresentado há algum tempo, foi-me até dito que um estudo foi feito, jamais achei o estudo, fi-lo eu mesmo com a ajuda da Wikipédia e sua excelente página da escalação de cada seleção de futebol.
Pus-me a anotar os meses de nascimento dos jogadores de futebol das seguintes seleções: Brasil, Paraguai, Chile e Argentina. Tomei a escalação mais atual possível, para não haver privilégio de uma época ou outra. A razão de pegar apenas países do hemisfério sul ficará clara com os resultados.
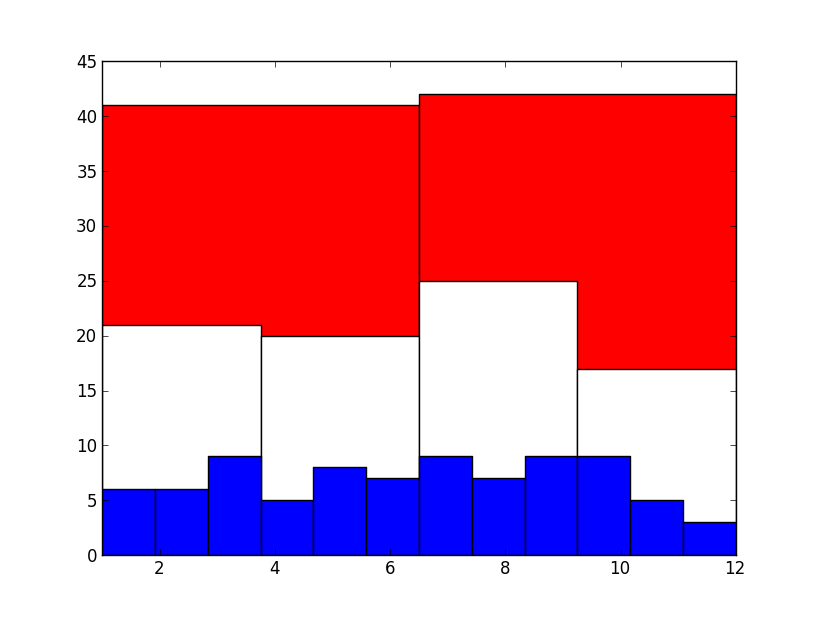
Enquanto o Paraguai não apresenta uma distribuição de nascimento de seus jogadores ao decorrer do ano que chame a atenção, Brasil, Chile e Argentina impressionaram-me e comprovaram, em termos nada rigorosos, a teoria que eu havia ouvido a respeito do estudo. Organizei um histograma em três camadas, as barras menores são os nascimentos no mês, as intermediárias representam nascimentos em um trimestre e as grandes são os nascimentos no semestre. O resultado do Paraguai, analisados 83 jogares, foi:
Nada impressionante até aqui, os aniversários parecem razoavelmente bem distribuídos em todos os níveis e não consigo perceber uma tendência evidente. No entanto, a distribuição do Brasil já começa a apresentar um fenômeno interessante:
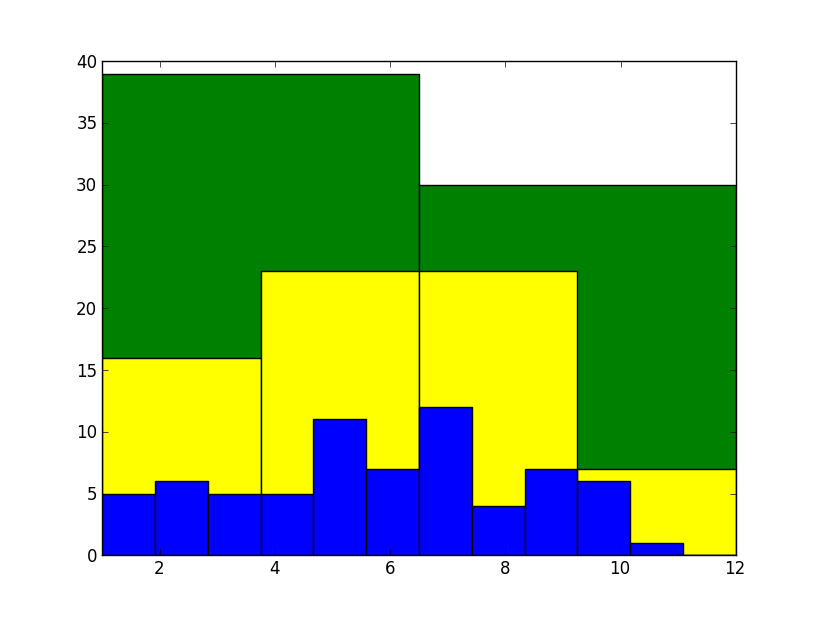
Temos na seleção brasileira, analisados os 69 últimos convocados de Mano Menezes, uma concentração clara de nascimentos no primeiro semestre, em especial uma forte ausência de nascidos no último trimestre do ano. Claro, isso pode ser uma improbabilidade realizada, não um indício de variável escondida. Se analisarmos com cuidado, podemos calcular a probabilidade de, jogando aniversários aleatoriamente no ano, ter essa diferença entre o primeiro e o segundo semestre; é improvável, mas nem de longe impossível.
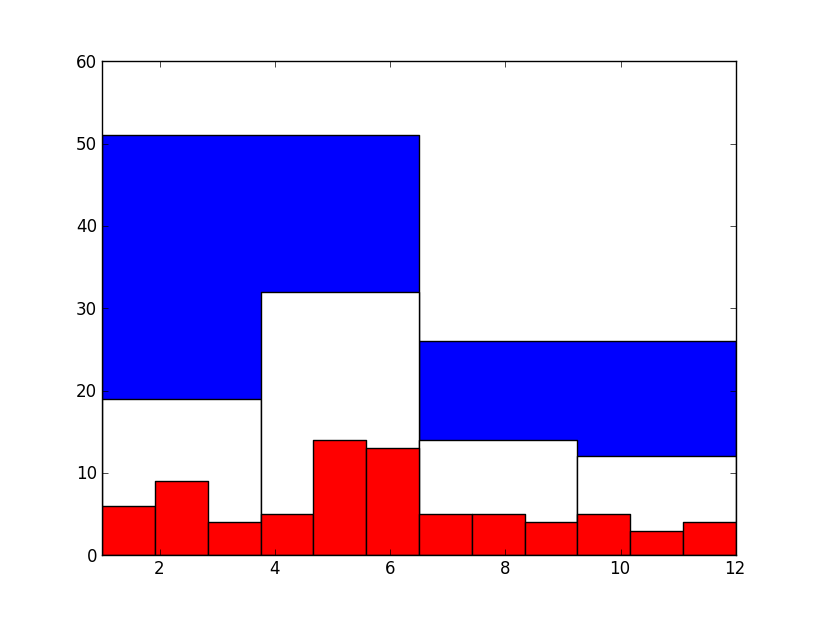
No entanto, os resultados do Chile, analisados 77 jogadores, revelaram-se:
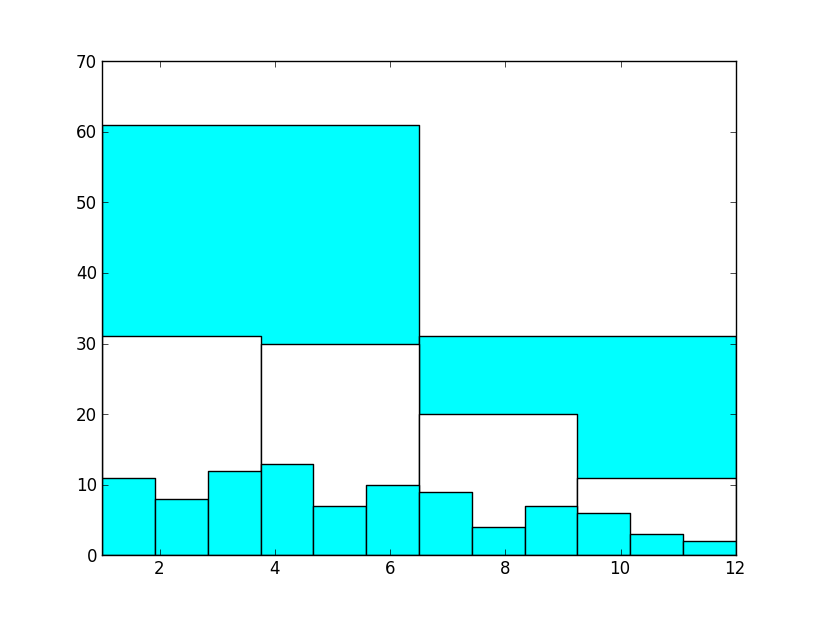
E essa diferença entre primeiro e segundo semestre já não pode mais ser explicada como uma anomalia estatística, há algo estranho nesse país que faz jogadores de futebol nascerem no começo do ano e não no final. Para confirmar a teoria, podemos avançar no estudo da seleção Argentina, analisando 92 jogadores:
Esse gráfico não pode, de maneira alguma, ser justificado como coincidência. A albiceleste possui o dobro de jogadores nascidos no primeiro semestre em relação ao segundo semestre. Entrementes, notamos que em todas as seleções dezembro é sistematicamente o pior mês, ou o segundo pior, no caso do Chile.
Podemos nos divertir calculando a probabilidade de obter uma configuração como a da Argentina se os aniversários fossem distribuídos de maneira uniforme no ano. Temos 92 jogadores e queremos saber a chance de, distribuindo aleatoriamente no ano, ter uma diferença de 30 nascimentos entre os dois semestres, sendo o primeiro semestre o favorecido. Calculando com cuidado, essa probabilidade não passa do valor 0,08%, extremamente baixa, ela precisa de uma explicação.
Antes que os astrólogos saiam em defesa de alguma correlação entre estrelas e seres humanos, comento a conclusão a que chegaram os estatísticos. Essa predominância de nascimentos em um semestre não ocorre em países europeus, curiosamente, analisei França e Inglaterra e os resultados não são nada impressionantes. Esses três países do sul, Brasil, Argentina e Chile, apresentam sistematicamente jogadores nascidos em um semestre, e a razão disso, muito provavelmente, é o ano letivo.
No mesmo argumento que usou Malcolm Gladwell em seu livro Outliers para explicar jogadores de hóquei, nesses países, as escolas de futebol organizam os alunos de acordo com o ano letivo, e os jogadores profissionais enfrentam peneiras desde cedo para seguir na carreira. Os nascidos no começo do ano são, por isso, os mais velhos de suas turmas e, ao enfrentam peneiras desde crianças, são também os mais fortes e mais rápidos. Os nascidos no primeiro trimestre são quase um ano mais velhos que os nascidos no último, e são selecionados em uma idade em que um ano é muito para o desenvolvimento corporal. Esse resultado é ausente nos times europeus porque as escolas de futebol não seguem um ano específico, algumas tomam o escolar como base e outras o ano de nascimento, não havendo consenso, há equilíbrio na distribuição.
Falta, claro, explicar o caso do Paraguai. Tendo em vista os outros países, o mais natural é supor, ou que o Paraguai é a anomalia estatística, ou que o sistema de escola de futebol e peneira desde muito cedo não é tão rigoroso no Paraguai.
Tudo o que eu acabo de fazer, aviso, consiste em estatística de péssima qualidade. Eu precisaria tomar vergonha na cara, analisar mais jogadores de mais times, informar-me sobre o sistema de avaliação do Paraguai e não me ater a essa tese com muito afinco, ela pode muito bem estar furada. Contudo, os 0,08% chamam a atenção, e confirmam que o estudo do paradoxo do aniversário não pode ser realizado com jogadores de futebol.
Claro que a hipótese feita, a distribuição igual de nascimentos ao redor do ano pela população normal, precisa ser justificada. Redireciono-os ao trabalho desse site, enquanto aponto ao curioso fato do grande número de nascimentos em setembro-agosto, provavelmente resultado das férias de natal, quando a chance de se estar em casa é alta e a programação da televisão cai de qualidade vertiginosamente.
Se o futebol sul-americano já apresenta esse fenômeno, podemos encontrá-lo de forma ainda mais acentuada em esportes cuja dependência da disposição física (e, logo, da idade) seja maior, o hóquei é um bom exemplo. Um grande estudo nesse aspecto foi realizado no Canadá em 1988 e os resultados do estudo são impressionantes, o mês de nascimento parece ter implicação direta no sucesso do jogador. Atualmente, parece que as ligas americanas e canadenses adaptaram um calendário diferente, mais próximo daquele europeu de futebol, e a diferença não é mais gritante.
E esses gráficos nos inspiram a questionar o quanto do sucesso de alguém em uma carreira é fruto de sucesso inicial, de ter se dado bem no começo, gostado, continuado, se esforçado e se dado ainda melhor, um círculo vicioso positivo vindo apenas do fato de ter sido bem sucedido no começo. Extrapolando, podemos nos perguntar se fazemos o que fazemos pelo sucesso inicial, e me pergunto quanto da matemática que faço não vem de uma primeira nota alta na matéria. As coisas talvez tivessem sido diferentes se eu tivesse errado mais questões, se minha professora fosse uma carrasca, se a ponta de meu lápis tivesse quebrado naquela primeira prova ou, quem sabe, se eu tivesse nascido em junho.

Feliz aniversário, Ricardo!
Tu conseguiria pensar em uma aplicação deste paradoxo à Física? Pois à Química, eu já tenho pra te mostrar:
Bimestralmente, o periódico Analytical and Bioanalytical Chemistry (Springer) lança problemas numa seção denominada Analytical Challenge. Em um artigo publicado em 07/12/2007, ‘Birthday chromatography challenge’, Juris Meija fala de uma aplicação deste paradoxo à Química Analítica, mais precisamente, à Cromatografia. Pra quem não sabe, cromatografia é uma técnica (muito versátil) de separação de substâncias na qual se passa a mistura através de uma coluna, input, esperando no outro lado saírem as substâncias puras, output (caso ideal, obviamente).
Pois bem, o autor do artigo propõe a pergunta “Qual a probabilidade de se separar todos os compostos de uma mistura multi-componente?”, mais especificamente, “Quantos compostos, em relação à capacidade teórica da coluna, podemos realmente esperar que se separem?”
Foi um artigo deste cara (um letão de pouco mais de 30 anos que já assume cargo em comissões da IUPAC) no Journal of Chemical Education que me fez ir atrás do e-mail dele e procurar aplicações não-triviais da Matemática à Química.
Grande abraço, Ricardo!
Do questionamento de quanto de nosso sucesso é fruto de um golpe de sorte no início da carreira, vou aproveitar a deixa pra comentar sobre o efeito de regressão à média analisado por Daniel Kahneman, Nobel de Economia de 2002.
Kahneman certa vez deu uma longa palestra a instrutores de vôo tentando convencê-los de que, no processo de aprendizado de seus alunos, elogios a bons desempenhos surtem um efeito maior que punição por falhas. Ao fim do discurso, um dos instrutores retrucou que, em seus vários anos de experiência, sempre que elogiava um piloto por uma manobra espetacular, na próxima vez ele piorava, mas a cada bronca que dava por um ato falho, ele observava uma nítida melhora na tentiva subsequente.
O ponto deste instrutor levou por água abaixo a palestra de Kahneman, ainda que este tenha tentado exemplificar o caso de regressão à média, dizendo que após a medida de um evento anormalmente acima da média, a próxima medida tenderia a piorar e retornar à média, ao passo que o desempenho após uma medida anormalmente baixa tenderia a melhorar na próxima.
As palavras do próprio Kahneman podem ser encontradas no artigo da wiki “Regression toward the mean”. Um trecho que achei interessante foi:
“This was a joyous moment, in which I understood an important truth about the world: because we tend to reward others when they do well and punish them when they do badly, and because there is regression to the mean, it is part of the human condition that we are statistically punished for rewarding others and rewarded for punishing them.”
De fato, eu acredito que primeiros acontecimentos bem sucedidos e bem recompensados possam sim aumentar a motivação das pessoas, e que elas talvez não tenham sentido muito o efeito da regressão à média, por alguma ou outra razão. No caso da matemática, talvez porque acabaram por estudar bastante antes de fazerem a próxima prova e puderam manter o sucesso.
Pingback: Férias | Todas as configurações possíveis
Pingback: Há partidos políticos no Brasil? | Todas as configurações possíveis
Achei sua hipótese pra lá de interessante, entretanto acredito haver uma outra mais “maliciosa”. Há, especialmente em clubes pequenos da AL, certo costume de alterar datas de aniversários de jogadores. Em geral jovens pobres e sem escolaridade, costumam “perder” uns meses de vida e ganhar certidão de nascimento nova com data no começo do ano – ou seja, jovens nascidos no fim do segundo semestre ganham novas certidões para o começo do ano subsequente de modo a ganhar mais um ano em cada categoria de base.
Um outro ponto legal de observar no brasil se dá pelo baby boom sazonal brasileiro. Os meses de maio e outubro coincidem com períodos de fecundação nas festas (dezembro/janeiro, carnaval e julho). Olhar data datas e estimar os 9 meses anteriores pode ser interessante tb.
Eu pensei na hipótese do Baby Boom, mas dei uma olhada nas taxas de fertilidade mensais brasileiras e vi que a diferença não chegava a 10% entre os meses, então é difícil explicar usando isso. Quanto à hipótese da mudança de data, admito que ela pode inserir uma flutuação na medida, mas não tenho base de dados para confirmar que seja um efeito significativo. Não posso dizer nem que sim, nem que não.
Justo!! De todo modo, parabéns pelo blog, muito bom!
Parabéns pelo esforço. O Malcolm Gladwell também apontou essa “concidência” nos jogadores de hockey canadenses, no livro Outliers:
“Barnsley went home that night and looked up the birth dates of as many professional hockey players as he could find. He saw the same pattern. Barnsley, his wife, and a col- league, A. H. Thompson, then gathered statistics on every player in the Ontario Junior Hockey League. The story was the same. More players were born in January than in any other month, and by an overwhelming margin. The second most frequent birth month? February. The third? March. Barnsley found that there were nearly five and a half times as many Ontario Junior Hockey League play- ers born in January as were born in November. ”
A razão, ele aponta:
“The explanation for this is quite simple. It has nothing to do with astrology, nor is there anything magical about the first three months of the year. It’s simply that in Canada the eligibility cutoff for age-class hockey is January I. A boy who turns ten on January 2 , then, could be playing alongside someone who doesn’t turn ten until the end of the year-and at that age, in preadolescence, a twelve- month gap in age represents an enormous difference in physical maturity.”
Continue obcecando hehe
Sem dúvida, foi de onde tirei a explicação, ou melhor, de onde eu li tirou a explicação, porque não conhecia a referência diretamente. Agora estará devidamente referenciado, muito obrigado.
Legal o estudo com as datas de aniversário no futebol. O livro que comenta sobre esse fenómeno é o Outliers, de Malcoln Gladwell.
Sim! Não lembrava a referência exata, só sabia que o estudo havia sido feito. Vou incluir no post, muito obrigado.
Gostei muito de ver os gráficos. Eu conhecia inderetamente os resultados e escrevi (http://sro0.wordpress.com/2006/11/16/genio-nao-e-por-acaso/) sobre o compêndio que compilou alguns resultados:
The Cambridge Handbook of Expertise and Expert Performance (Cambridge Handbooks in Psychology)
by K. Anders Ericsson
Link: http://amzn.com/052184097X
Cara, seu conteúdo é muito bom! Não tem uma página no facebook para eu acompanhar suas atualizações? Não uso coisas de RSS 🙂
Abraço e parabéns!
OBS: Eu já li o Outliers e é um livro incrível!
http://www.facebook.com/TodasAsConfiguracoesPossiveis
Muito obrigado! Preciso ler esse livro.
Muito legal o texto. Fiquei com uma dúvida no entanto. Se o motivo da distribuição “estranha””de Brasil, Argentina e Chile for de fato o que você comenta no texto não deveriamos ver também uma concentração diferente de nascimentos por trimestre (e até por mês). Por exemplo, os jogadores nascidos no primeiro trimestre não deveriam ser mais numerosos que os do segundo tri, e esses mais numerosos do que os do terceiro tri e assim por diante. Nos dados que você mostrou parece que isso até acontece ligeiramente na Argentina, mas no Brasil e no Chile está longe de ser o caso.
Uma diferença por trimestre não tem tanta razão de ser significativa, porque três meses não são uma diferença tão grande na idade física de uma criança ou pré-adolescente. A distribuição do Chile de fato é a mais estranha, mas a chance de haver uma diferença desse calibre entre os trimestres, supondo uma distribuição aleatória, é de 5%, o que não é alto, mas não são aqueles 0,08% da comparação dos semestres. Você pode ter razão, nesse mato pode haver coelho, mas, se há, não consegui achar.
Esse assunto dos aniversários me lembrou algo engraçado. Minha prima certa vez passou alguns dias em um cruzeiro, e lá pela terceira noite resolveu “duvidar” da veracidade de tantos aniversários que eram comemorados todas as noites, na hora do jantar e nos bares do navio. Ela sugeriu que as pessoas estariam inventando aniversários, como uma molecagem entre amigos.
Meu tio rapidamente deu a solução matemática para a questão. Em um navio com 5000 pessoas, seria de se esperar uma média de 13 a 14 pessoas fazendo aniversário por dia (e claro, comemorando com a família e os amigos). em 5 dias de cruzeiro, teria cerca de 68 pessoas aniversariando.
Eu quando ouvi a história ainda imaginei um desvio na estatística, para um número ainda maior de aniversariantes: as pessoas que compraram o passeio do cruzeiro podem tê-lo feito justamente para comemorar o aniversário, seu ou de um familiar, amigo, etc.
Será que estávamos certos?
Adorei o post, e também o blog do autor. Parabéns!
Eu arrisco dizer que estavam. Muito obrigado!
Pingback: Política: um sistema anti-frágil » “Direita? Esquerda? É tudo igual”