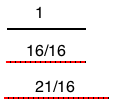Arquivo mensais:abril 2012

Um diagrama nada claro

Rookie

Na faculdade, aprendemos a física por sua trajetória histórica: começamos pelas leis de Newton, sua mecânica, passamos ao estudo de ondas, óptica, termodinâmica, atravessamos o eletromagnetismo e terminamos a “física básica” com quântica. Mais para o final do curso, continuamos com a física do século XX, da qual a quântica faz parte, além de incluir a física estatística e a relatividade geral nessa história. Matérias mais avançadas, como a teoria quântica de campos (TQC) e a teoria estatística de campos (TEC) são assunto de mestrado e doutorado, muita gente parece viver bem feliz sem jamais tocar em um livro de qualquer dessas matérias.

Mas a relação entre as áreas da física não é essa histórica, uma não leva naturalmente a outra. É possível ser muito feliz em uma área da física sem jamais precisar se aprofundar muito em outra (ainda que grandes descobertas costumem ser feitas apenas por físicos com um vasto conhecimento de quase todas as áreas), não preciso saber astronomia para trabalhar com física do estado sólido (ou física dos materiais).

Então decidi tomar alguns minutos, sentar e pensar em um diagrama mais compreensivo da física, que leve em conta as interconexões entre as áreas e que seja uma divisão justa e organizada dessa ciência. É evidente que cheguei a algo bem confuso, mas o resultado não ficou feio, e coloco-o aqui.

Muitos físicos vão discordar com ferocidade da divisão e organização, mas foi o melhor que pude, não conheço tanto de todas as áreas para entrar em uma reflexão mais profunda que o que escrevo nesse post.

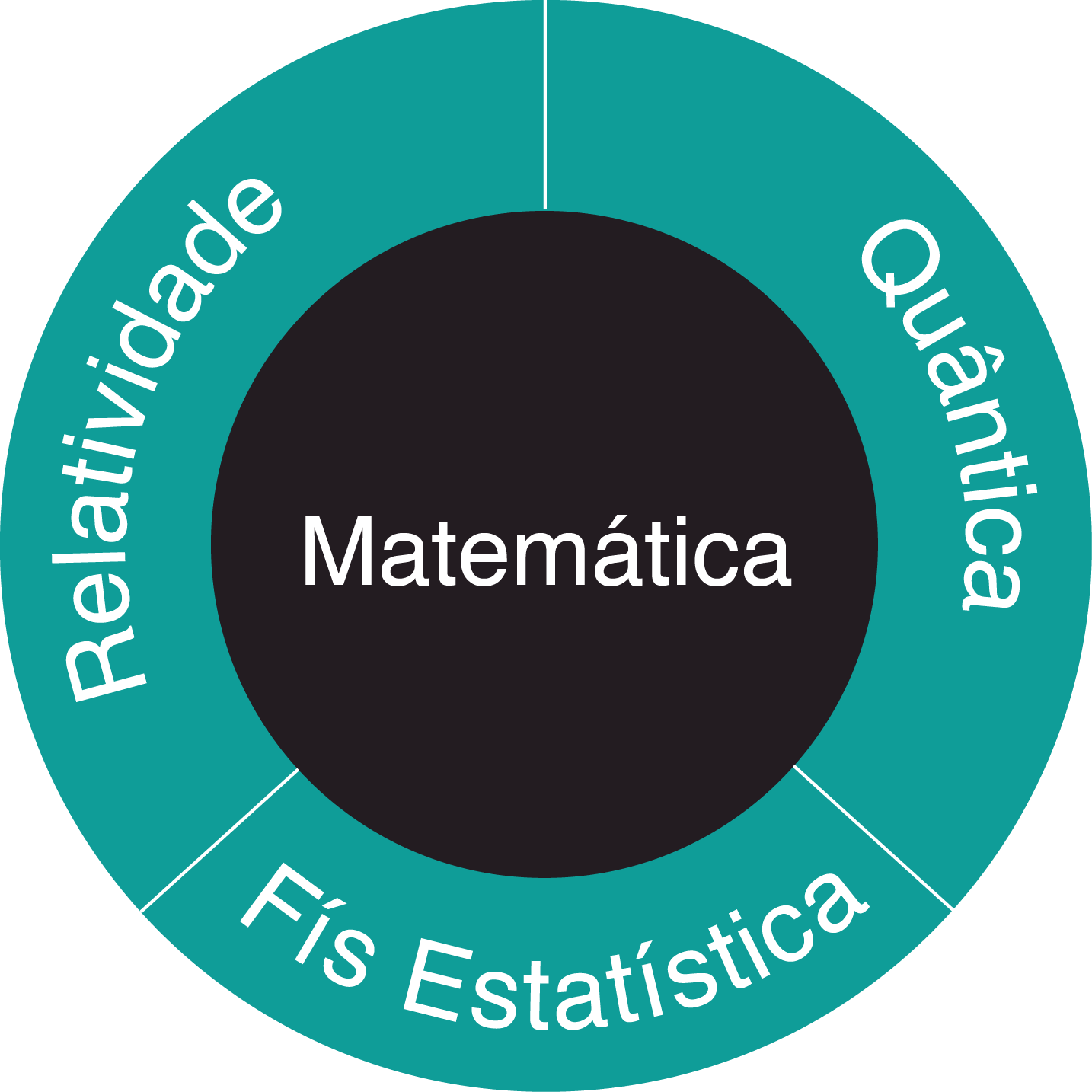
Comecei colocando a matemática como centro. A física é inteira apoiada na matemática, e nela estão muitos dos vínculos das áreas da física. Em seguida, tracei as três principais áreas da física: relatividade (geral ou restrita), física estatística e física quântica.

Física quântica: é o estudo do muito pequeno, muito mesmo. Estamos falando de elétrons, prótons, átomos, nada que possamos ver ou tocar diretamente, precisamos estar pelo menos a 0,00001 mm ($10^{-8}$m) para começar a sentir algum efeito dos estudos dessa área. Ainda, é o que precisamos estudar para entender do que as coisas são feitas, como fazer coisas novas, materiais novos, entender as leis que regem a escala atômica e usá-las.

Relatividade: estudamos os efeitos de velocidades muito altas (próximas às da luz, que é a máxima possível), massas muito grandes (como a da Terra ou a do Sol) e energias muito elevadas (como a explosão de uma estrela).

Física estatística: é a área que tenta deduzir, a partir do mundo do muito pequeno, o que acontecerá no nosso mundo. Tentamos entender como a gota de água tende a ficar junta se ela é feita de várias moléculas, ou como não conseguimos atravessar a parede se o espaço entre os átomos é muito maior que os átomos.

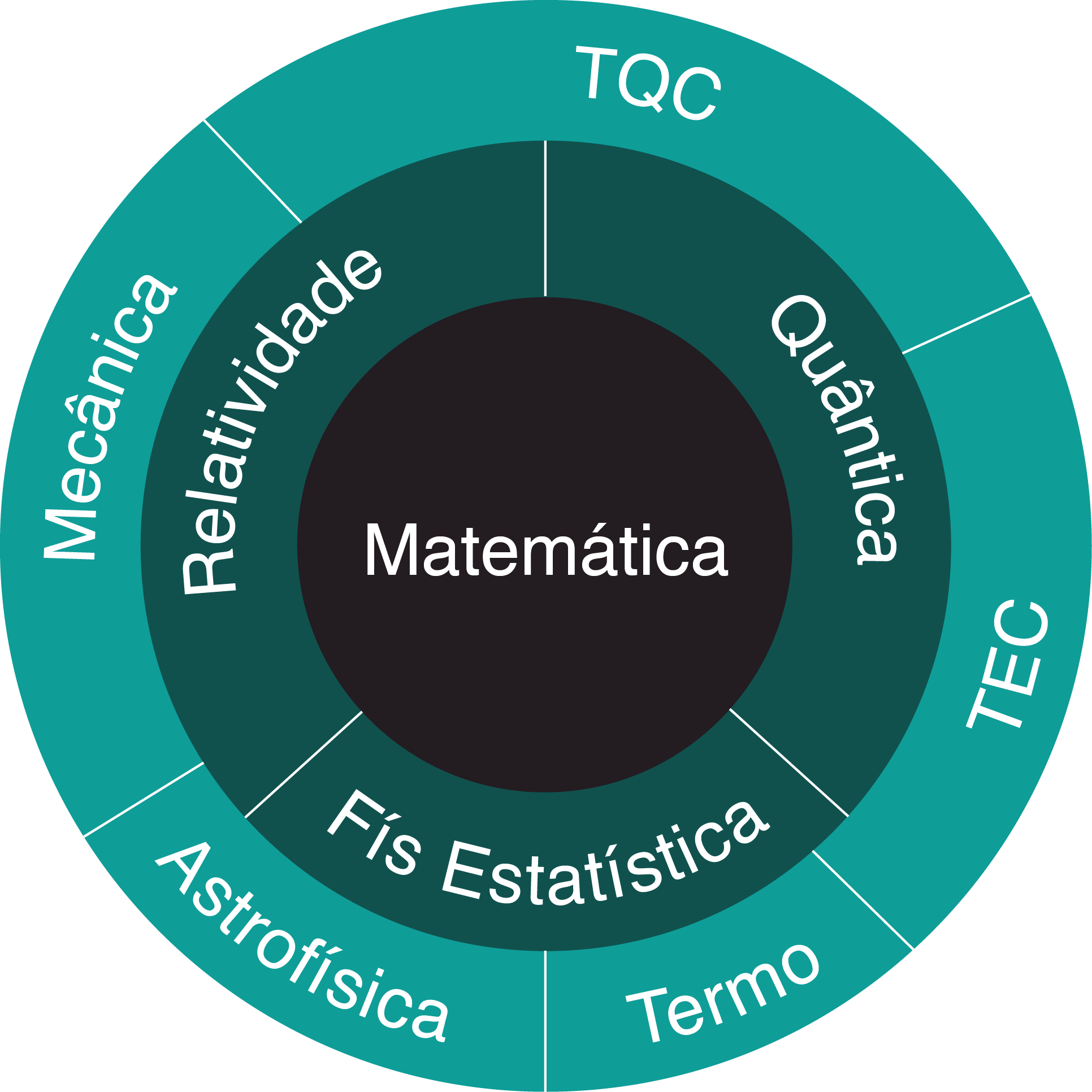
Assim, posso explorar as intersecções entre essas áreas. Se estamos na fronteira entre relatividade e quântica, estamos falando da teoria quântica de campos (TQC), uma área bem complicada que tenta escrever a mecânica quântica em uma linguagem que leve a relatividade em conta. Não me atrevo a tentar misturar relatividade geral com quântica, ninguém consegue fazer isso decentemente. Entre a física estatística e a quântica, teremos a teoria estatística de campos (TEC), que usa diversas propriedades do mundo do muito pequeno para explicar muito fenômenos do nosso cotidiano, em uma linguagem matemática bem trabalhada e bem parecida com a da TQC. Eu poderia colocar tudo em uma área só, campos, mas assim fica mais fácil de ver.

Entre a relatividade e a física estatística, temos a astrofísica, o estudo das propriedades físicas das estrelas, galáxias, que exige tanto conhecimento de relatividade, por reger as leis fundamentais desses corpos, como conhecimentos da física estatística, porque uma estrela é formada de muitos átomos e uma galáxia de muitas estrelas. A relatividade, sozinha, inclui a nossa querida mecânica do colegial, que é apenas um caso particular da relatividade para baixar velocidades e massas suficientemente pequenas. A física estatística, quando aplicada a gases e líquidos, torna-se a termodinâmica.

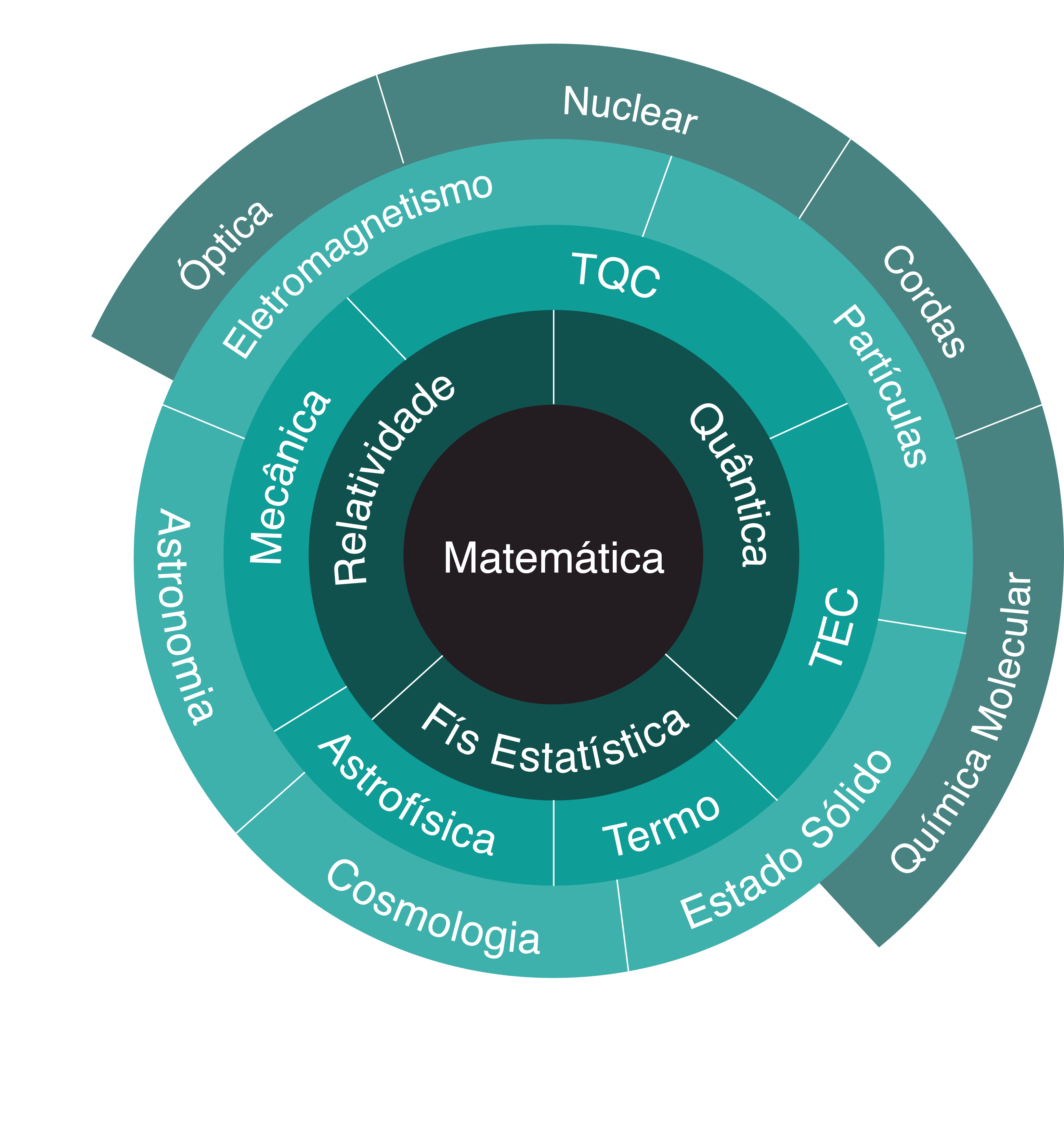
Se continuamos, podemos pensar que o estudo das propriedades físicas dos corpos celestes aliado às leis de Newton nos permite saber a posição, trajetória e diversas outras grandezas estudadas pela astronomia. A astrofísica, quando estudada em grande escala e recebendo o apoio das leis da termodinâmica e da física estatística, torna-se a cosmologia: o estudo do universo como um todo, sua expansão, evolução e destino. Aplicar a teoria estatística de campos à termodinâmica nos torna capazes de descrever estruturas mais complexas que gases, podemos até pensar em cristais, coloides, plásticos, estamos na física do estado sólido. A teoria quântica de campos e a teoria estatística de campos se encontram para descrever propriedades complicadas do mundo subatômico, permitindo-nos estudar a física de partículas. Por fim, a teoria quântica de campos, capaz de descrever os elétrons e os prótons (que possuem carga) e a mecânica de Newton se encontram no eletromagnetismo.

Por fim, podemos colocar algumas outras áreas. O eletromagnetismo é muitas vezes estudado profundamente no aspecto de transmissão de energia eletromagnética em forma de onda, uma área conhecida como óptica, que engloba toda a propagação de ondas eletromagnéticas no vácuo ou não. A física do estado sólido e a de partículas se encontram para tentar gerar materiais novos, diferentes, estruturas moleculares complicadas, e podemos atribuir esse estudo à química molecular, que não é tanto física assim, mas merecia um lugar no diagrama. As partículas e o eletromagnetismo juntam forças para desbravar os mistérios do centro do átomo, em uma área muito ativa no último século chamada física nuclear. E das partículas, sozinha e um pouco isolada, quase uma sub-área da matemática, parte a teoria das cordas.

Qual a lógica do diagrama? Se você quiser estudar alguma área, terá que saber bastante de todas as áreas internas à que escolheu, estudando todas as que sua área toca no anel interior. Claro, isso não torna as áreas exteriores mais difíceis, você muitas vezes não precisa se especializar nas áreas interiores para saber a sua, é apenas um diagrama que indica vínculo, procedência e contato entre as áreas. Queria que o diagrama terminasse com um anel completo, mas não consegui pensar em nada que viesse de estado sólido e cosmologia, ou nada melhor para colocar entre astronomia e cosmologia que “coisas do espaço”.

4 respostas

A unicidade do funil

Geek

Um de meus teoremas favoritos, e talvez um dos mais úteis que conheço, é o de Cauchy-Lipchitz. Não só sua demonstração é extremamente divertida, e pode ser vista entre as páginas 23 e 26 deste texto, ele é extremamente poderoso e dá-nos a segurança de afirmar existência e unicidade da solução de diversas equações diferenciais.

Teorema (de Cauchy-Lipschitz). Seja $f=f(y(x),x)$ uma função contínua em $x$ e localmente lipschitziana em $y$ no ponto $y_0$. Seja $y(x_0) = y_0$. Então existe um intervalo $[x_0-\varepsilon, x_0+\varepsilon]$ tal que a equação diferencial

\[\frac{dy(x)}{dx}=f(y(x),x)\]

possui solução única.

Esse teorema é bem forte, já que as condições não são tão exigentes. Todas as funções elementares são contínuas nos pontos de seu domínio, e a condição de localmente lipschitziana, um pouco mais forte, também não é difícil de obter, basta ter uma primeira derivada que não divirja em um dado ponto que a função já é localmente lipschitziana naquele ponto. Em uma explicação grosseira, essa propriedade é o equivalente a exigir um “crescimento controlado” da função, naturalmente funções cujas derivadas primeiras divergem não são nada controladas.

E para provar que toda função contínua cuja primeira derivada não diverge é localmente lipschitziana basta escrever o teorema do valor médio e perceber que ele é exatamente a definição de uma função localmente lipschitziana.

Mas esse post não é sobre resultados da análise real, que são interessantes, mas sobre o problema do funil, conhecido também como clepsidra. Nele, tentamos estudar a velocidade com que a água desce um funil. Chamamos a velocidade no topo da coluna de água $v_A$, sua velocidade na saída de $v_B$, e as superfícies do topo e da saída de $S_A$ e $S_B$ respectivamente. Orientamos a altura no sentido evidente, com a origem na base do funil.

Podemos usar a equação de Bernoulli entre os extremos da água:

\[ \frac{1}{2}\rho v_A^2+\rho gh=\frac{1}{2}\rho v_b^2\]

\[v_A^2=2\left(1-\frac{S_B^2}{S_A^2}\right) gh=2\alpha gh.\]

Notem que eu também usei a equação da conservação da massa, em que $S_Av_A=S_Bv_B$, para isolar a velocidade em A. No final, temos uma equação que relaciona a altura da coluna de água com a sua velocidade:

\[ \frac{dh(t)}{dt}=\sqrt{2\alpha gh}.\]

Para obter uma solução, precisamos de uma condição inicial. E eis o nosso problema. Eu posso dar diversas condições iniciais, valores de $h(t)$, que equivalem à altura da água no instante inicial, mas uma delas, em particular, me incomodará muito: $h(0)=0$. A função $ \sqrt{x}$ não é localmente lipschitziana em zero (notem que a derivada explode, mas a explosão da derivada é apenas condição suficiente, eu teria que provar com mais calma), o teorema de Cauchy-Lipschitz não se aplica a ela se a condição inicial for dada com $h$ valendo zero!

O que é completamente esperado, pois, se eu te contar que agora o funil está vazio ($ h(0)=0$), você não pode me dizer nada sobre a história do funil (obter $h(t)$). Ele pode ter esvaziado há dez segundos (ou seja, $h(-11)$ seria diferente de zero), há três minutos, há horas, dias, pode nunca ter sido cheio (solução $h\equiv 0$); a perda da condição de localmente lipschitziana nos tira a unicidade da solução, e isso é completamente esperado: saber que o funil está vazio nada nos diz sobre quando ele esvaziou!

E essa aplicação curta, bela e tremendamente real do teorema de Cauchy-Lipscitz o torna um de meus favoritos das equações diferenciais, sendo ele já um dos mais úteis. Ao encontrar uma dessas, não hesite, veja a primeira derivada, veja a continuidade, e respire aliviado. Alguma solução existe, e é única. Isso, a um matemático, já é ter a equação quase completamente resolvida, o resto são detalhes.

2 respostas

A raiz do problema

Rookie

O teorema de Pitágoras é o centro da geometria de nossa oitava série, agora nono ano. Nele, aprendemos que há uma relação simples e até bonita entre os lados de um triângulo retângulo, aquele com um ângulo de 90°. O que não nos contam é a quantidade de problema que esse teorema já deu, e até as mortes que causou, na época de seu descobrimento. Os número irracionais já foram muito mais interessantes, quando havia gente que daria a vida, e mataria, para manter certas verdades ocultas na antiguidade clássica.

Pitágoras é uma figura historicamente bem misteriosa. Tudo o que se sabe sobre ele provém de séculos depois de sua morte, há mesmo quem duvide de sua existência, e todos os dados sobre ele são carregados de misticismo. Isso porque Pitágoras não era apenas um matemático, um professor, um sábio, ele foi além: em sua busca por conhecimentos e verdades nos números, enxergou um pouco mais do que devia e fundou um culto religioso envolvendo as verdades geométricas do universo.

Neste culto secreto, ciência e religião não possuíam diferença alguma e a busca pela verdade era também a busca pelo divino. O culto possuía regras de alimentação, comportamento, ser pitagórico era muito mais que pesquisar matemática, era um estilo de vida, e seu seguidores reuniam-se em uma mistura de escola com monastério no sul da atual Itália, no século V a.C.

Essa mistura não podia terminar muito bem. Diz-se na boca pequena, nesses boatos da história da matemática, que um infortunado descobriu que a raiz quadrada no número dois era um número irracional. Horrorizados com a notícia, os pitagóricos, e talvez até o próprio Pitágoras, mandaram matar este matemático para silenciar o que colocaria em cheque muito das verdades divinas descobertas pelo grupo. A razão do choque é difícil entender, mas vamos tentar, ela reside na ideia que os gregos tinham da natureza de um número.

Toda a matemática grega repousava na geometria, sua álgebra era fraca, a escrita era sempre feita em termos geométricos e os grandes trabalhos gregos versavam teoremas avançados sobre elipses, cônicas, parábolas, mas a ideia de equação está ausente em todos esses textos. Os números, como eles entendiam, eram sempre dados por proporções. Eles escolhiam um comprimento de linha, uma barra, para ser o 1. Mas isso não era “apenas” o número 1, a própria noção de número não existia muito, o 1 da contagem de ovelhas e o 1 da barra eram coisas diferentes para os pitagóricos, e gregos em geral. Essa barra de tamanho 1 representava a unidade, o fundamental, o que gera todas as coisas. E a definição de número dos gregos estava atrelada a isso. Dizer o número 3, a eles, era a barra cujo comprimento era três vezes o da barra unidade. Na ideia deles, dizer 3 era dizer:

Os demais números eram compostos de maneira parecida. A fração 21/16, por exemplo, não era ensinada com pedaços de bolo como em nossas quarta-séries, mas com pedaços da unidade. Você quebra a unidade em 16 pedaços, junta 21 deles, cola e tem o número que deseja:

E assim eles faziam a matemática. Toda barra encontrada era “numerizada” quando se quebrava a unidade em partes pequenas o suficiente para, com um bom número delas, colar e formar a barra nova. E todo número novo era sempre pensado em forma de barra ou de pedaços de barra, toda a matemática eram intersecções, retas, circunferências e pontos. Até que, um dia, um homem, dizem Hipaso de Metaponto, descobriu uma barra que não era número. E, pior, ela estava o tempo todo bem embaixo do nariz de todos. Essa barra é a raiz quadrada de dois, uma barra tão facilmente obtida quanto alguém pode desenhar um quadrado:

Essa barra, a diagonal do quadrado, não pode ser composta com pequenos pedaços da lateral do quadrado, por menores que esses pedaços sejam. Isso não é nada evidente, você pode até tentar se enganar com a fração 141/100, mas ela ainda não é perfeitamente a diagonal do quadrado e nenhuma outra fração jamais será. Se antes eles apenas achavam que era uma barra cuja fração era complicada demais, isso é um abismo em relação à ideia de “não há fração para essa barra”. Em outras palavras, isso violava a própria noção de número dos gregos, algo alienígena à matemática deles, que estava profundamente atrelada ao religioso, à noção de proveniência da unidade, da formação do todo pelo pedaço primordial, ora, nada mais natural que silenciar o herege que descobriu esse pedaço de barra infiel.

A maneira como ele descobriu isso foi geométrica, mas posso dar um argumento algébrico legal de como nenhuma fração ao quadrado dá dois. Suponha que eu seja malandro, suponha que eu tenha encontrado dois números $p$ e $q$ tais que $\left(\frac{p}{q}\right)^2=2$. Como eu estou estudando a fração, é de bom tom que $p$ e $q$ não tenham divisores em comum pois, se tiverem, basta dividir a fração em cima e embaixo pelo número para ter uma fração equivalente (ou seja, 10/15 é o mesmo que 2/3, basta eu dividir os dois por 5).

Mas se $ \left(\frac{p}{q}\right)^2=2$, então $ \frac{p^2}{q^2} = 2$ e $ p^2 = 2q^2$. Até aqui sem surpresas, apenas apliquei o quadrado nos dois elementos e passei o de baixo multiplicando. No entanto, se $ p^2$ é duas vezes alguém, ele tem que ser par. Mas se $ p^2$ é par, então $ p$ é par, pois o quadrado de um número só é par se o próprio número for par, não tem como fazer um fator 2 “surgir” quando você multiplica um número por ele mesmo. Então $ p$ é par, e, como todo bom número par, é o dobro de alguém. Vamos chamar esse alguém de $ k$, então $ p=2k$. E se $ p^2 = 2q^2$, podemos substituir esse $ p$ por $ 2k$ e escrever $ (2k)^2=2q^2\implies 4k^2=2q^2\implies 2k^2=q^2$. De novo, sem surpresas, eu apliquei o quadrado nos dois caras da esquerda, percebi que podia dividir os dois lados da equação por dois e o fiz. Então eu provo que $ q^2$ é o dobro de alguém, o tal do $ k^2$, e, com isso, é par, o que faz o próprio $ q$ ser par também. Moral da história, se $ \frac{p^2}{q^2} = 2$, então tanto $ p$ quanto $ q$ são pares.

Contudo, eu havia suposto que $ p$ e $ q$ não possuíam divisores em comum! E acabo de provar que ambos são pares, então eles possuem um divisor em comum. Ora, posso dividir ambos por dois que a fração $ \frac{p}{q}$ ainda terá dois como quadrado, mas eu posso repetir o raciocínio acima e novamente provar que eles ainda são pares, então posso dividir de novo por dois e, aplicando o raciocínio acima, provar que ainda são pares! Ora, nenhum número é infinitamente par, está na cara que caímos em contradição nesse raciocínio e isso prova que nossa hipótese inicial é falha, pois ela nos conduz a um absurdo, que é um número infinitamente par. A verdadeira moral da história é: não existem números $ p$ e $ q$ tais que $ \frac{p^2}{q^2} = 2$.

E isso prova de maneira definitiva que a diagonal do quadrado é um alienígena no mundo da matemática grega, um número que não pode ser colocado como razão entre dois outros e, nessa medida, justamente chamado de irracional. A existência de tais números foi mantida em segredo por um bom tempo, poucos queriam seguir o exemplo de Hipaso. Hoje, não apenas sabemos que eles estão por toda parte, mas que a maior parte dos números reais é, de fato, de número irracionais. Em outras palavras, se você tirar um número real ao acaso, a chance é zero de tirar um que pode ser colocado em forma de fração, mas uma definição com mais cuidado disso tudo levaria a outro post, mas um indício pode ser encontrado em um outro, mais antigo, sobre os infinitos, onde vocês podem comprovar que, se as frações entram em uma fila, o raiz de dois, este incompreendido, não entra em fila nenhuma.

4 respostas

As condições de Tchebychev

Geek

O post de hoje não é nada longo, mas um resultado que já me ajudou muitas vezes e nunca o vi em outro lugar além de no livro do Demidovich. E como todo o resto desse livro, ele não demonstra, então nunca vi uma justificativa para uma palavra específica daquele resultado, que desde sempre me atormenta. Um dos motivos de não ter encontrado, acho, foi o fato de Tchebychev ser escrito cada vez com uma ortografia diferente, de acordo com os caprichos do autor ou editor, o que escrevo é respeitando a grafia da tradução que tive do Demidovich.

Aos que não conhecem o livro, ele é um monstro russo de mais de mil exercícios espalhados pelas matérias de cálculo, é como uma tábua de multiplicação para o cálculo diferencial, um excelente treinamento de Kumon a quem quer ficar rápido nessas coisas. Ainda, nele encontrei um resultado simples e bem interessante, que hoje compartilho convosco.

Integrando funções na mão, sempre podemos nos deparar com a possibilidade de estar tentando realizar o impossível: encontrar uma primitiva a uma função que não possui primitiva. Poucos cursos de cálculos dão a devida atenção a essa diferença: primitivização e integração não são a mesma coisa. Enquanto é famoso o fato de que nem toda função integrável possua primitiva ($e^{-x^2}$ é o exemplo mais clássico), encontrar uma função F que derivada dê f (o processo de primitivização) não garante que a função seja integrável, apesar dos rumores. Esse exemplo no link é um pouco trabalhoso, e bem poderoso, é uma função com primitiva que não é integrável em lugar nenhum, um contra-exemplo bem interessante.

Mas não consigo me lembrar de nenhum teorema que consiga me dizer quando uma função possui ou não primitiva elementar, ou seja, quando vale a pena sair tentando transformações, integrações por partes ou separações de polinômios em uma função que não me dá chance de integrar, que não possui uma primitiva suficientemente simples para ser encontrada com minhas técnicas baratas de cálculo I. E as condições de Tchebychev são o único teorema desse tipo que já vi:

Condições de Tchebychev: Seja a integral:

\[\int x^m(a+bx^n)^pdx\]

Então esta integral pode ser expressa por meio de uma combinação finita de funções elementares somente nos seguintes casos:

  1. Quando $p$ é inteiro.
  2. Quando $\frac{m+1}{n}$ é um número inteiro. Nesse caso, use a substituição $a+bx^n = y^s$, onde $s$ é o denominador de $p$.
  3. Quando $ \frac{m+1}{n}+p$ é um número inteiro. Nesse caso, use a substituição $ ax^{-n}+b = y^s$, onde $s$ é o denominador de $ p$.

A palavra que me intriga nesse resultado é o somente, pois nunca vi teoremas ou lemas com manobras para provar que uma função não possui primitiva elementar, mas isso provavelmente é ignorância minha. Apesar de não conhecer as engrenagens desse teorema, o resultado é bem útil, e salvou-me a vida vez ou outra, possuindo um ar de mistério que, apesar de me incomodar, ainda me encanta um pouco.

2 respostas

Poeira das estrelas

Rookie

Perguntaram em uma entrevista ao grande astrofísico Neil deGrasse Tyson qual ele julgava o fato mais fascinante da ciência. Como bom físico, ele podia escolher de uma vasta gama de coisas impressionantes sobre a natureza e o universo, e decidiu pela grande jóia da astrofísica: a nucleossíntese dos átomos pesados. Esse nome parece impressionante e difícil, mas não conheço nenhum outro fato que seja tão impressionante, belo, poético e impactante quanto descobrir de onde vieram os elementos que compõem cada um de nós e o que nos cerca.

Em termos apenas científicos, não seria desonesto responder ao “de onde viemos” com a palavra “Big Bang”. Isso é verdade, mas é também uma resposta incompleta, o Big Bang produziu, no máximo, átomos de hidrogênio para todo o lado, e somos compostos de muito mais do que isso. A formação dos átomos de hidrogênio no Big Bang é um assunto também fascinante, a maneira como as reações químicas competem com a expansão do universo nesse período primordial é para ser assistida com pipoca, mas fica para outro post. Vamos entender como chegamos dos átomos de hidrogênio, o número 1, aos de urânio, número 92, passando por todos os que conhecemos da tabela periódica (exceto o tecnécio, número 43, que é instável, e isso é outro fato legal sobre a ciência).

Tudo começa há muito tempo atrás, em uma galáxia muito, muito distante, o hidrogênio que por lá havia se concentrou mais do que devia. Gases andam de um lado para o outro no universo, eles se atraem por força gravitacional e se dispersam pelo fenômeno normal de dispersão, como o cheiro de um perfume se dispersa em uma sala quando aberto o frasco. Mas se a concentração é forte o suficiente, sua gravidade vence essa dispersão e ele começa a se acumular, inicia o processo de formação de uma estrela.

O destino dessa estrela dependerá da quantidade de hidrogênio inicial, a menos de patologias (caso ela absorva mais gente, enfim, o espaço é uma selva, muita coisa pode acontecer). Vou descrever o processo de uma estrela bem massiva. O Sol não se enquadra nesse processo, ele irá parar em algum estágio intermediário para seguir algum outro destino, o que descrevo é a sina das estrelas massivas.

Aquele hidrogênio todo começa a se acumular, e o centro dele começa a ganhar pressão, um processo parecido a você apertar uma seringa cheia de ar e perceber que o que há dentro dela atinge uma tal pressão que você não consegue mais apertar. Com a estrela, esse aumento de pressão vem com aumento de temperatura, porque em matéria de volume ela não tem tanta escolha. Isso é resultado daquele $PV = nRT$ do seu colégio, com $P$ alto, $T$ tem que também ser alto. Em termos microscópicos, as partículas do interior da estrela tomam porrada (pressão gravitacional) de todas as que estão fora, elas acabam ganhando velocidade (temperatura) e dão porrada de volta, nada mais justo.

O problema é que a estrela brilha (na verdade, tudo brilha, eu e você brilhamos, mas isso fica para outro post), e esse brilho a faz perder energia. Em termos microscópicos, o hidrogênio em torno dela consegue ir mais perto do centro em algum momento (o que seria uma “queda” do hidrogênio, ele ganha velocidade), ele brilha, manda luz e perde velocidade, então não consegue voltar para a altura que estava. Toda a estrela, nesse processo, fica mais junta, e a pressão gravitacional no centro aumenta, aquele hidrogênio tem que ficar ainda mais quente para segurar todo o entorno da estrela que está mais próximo e batendo com mais vontade.

Temperatura é a velocidade média das partículas. Aquele hidrogênio do centro está tão rápido que, em uma manobra bem colocada, colide de frente com outro hidrogênio e eles formam hélio. Mas não é uma reação amigável, o choque causa uma liberação de energia muito grande. Em outras palavras, o hélio, quando se forma, está em alta velocidade de vibração e bate nos outros hidrogênios, aumentando a temperatura do local e segurando a pressão do resto da estrela. Esse processo acontece com diversos átomos de hidrogênio e logo o centro da estrela é composto de hélio, envolto em uma estrela toda de hidrogênio.

O hélio deve esquentar cada vez mais, para segurar aquela pressão sempre aumentando, pelo mesmo problema de antes. Em um momento, a temperatura do hélio é tão alta que ele pega outro de jeito e forma berílio, que rapidamente vai encontrar outro hélio e formar carbono. O berílio não aparece muito porque ele facilmente vira carbono, mas o carbono dificilmente vira outra coisa. Teremos, com isso, um núcleo de carbono envolto em uma camada de hélio rodeada de hidrogênio, nossa estrela será uma cebola de elementos, com o centro mais pesado que as bordas.

E assim continuaremos, com um centro sempre aquecendo e novos elementos colidindo e se formando. Esse ciclo continua até a formação do ferro (na verdade, acho que vai até o níquel, mas ele rapidamente vira ferro) e teremos uma estrela gigantesca em diversas camadas de elementos como uma cebola, cuja figura fica mais ou menos assim:

Mas se enganam os que acham que nossa fábrica de átomos continuará esse processo até o urânio. A partir do ferro, a fusão de dois elementos não libera mais energia; não há aquela história de colidir dois e aumentar a velocidade. Aos que se lembram da química, dizemos que a partir do ferro a reação de fusão torna-se endotérmica. Com isso, a estrela para por aí, com um grande e crescente núcleo de ferro.

Mas não somente há outros elementos na natureza como você é feito de alguns deles (o zinco e o iodo, por exemplo). Podemos, contudo, já perceber que esse mecanismo explica a grande abundância de elementos mais leves que o ferro na natureza, inclusive a abundância de ferro, e a raridade dos mais pesados, como o ouro, a prata e a platina. O sistema de produção dos elementos mais pesados era um mistério, até proporem que esses elementos são formados na morte das estrelas.

Esse processo não continuaria infinitamente. A temperatura no núcleo de ferro chegaria a valores tão altos que algumas reações impensáveis na nossa realidade começariam a acontecer, uma delas é a união de elétrons com prótons para formar nêutrons. Não é muito famoso o fato de nêutrons não serem caras que, sozinhos, são estáveis, eles levam em média 15 minutos para virarem um próton e um elétron. Mas se a temperatura está muito alta, o processo inverso pode acontecer, e acontece. O problema é que quem segurava a pressão da estrela toda eram os elétrons, eles sumindo, o núcleo colapsa: todo aquele núcleo de ferro é completamente vencido por sua gravidade e se comprime em uma densidade tão impressionante que você conseguiria enfiar uma caminhote em um dedal, ou o Sol em uma bola de 10Km. A única coisa que impede o núcleo de se contrair ainda mais com sua gravidade é a força forte, em outras palavras, a densidade dessa massa é a mesma da densidade do núcleo de um átomo: a maior que é possível atingir.

Então temos isso: um núcleo comprimido ao extremo pela força gravitacional que vai puxar todo o resto da estrela para si. Esse resto, as outras camadas da cebola, será puxado com extrema violência e, assim que a primeira camada colide com o centro, ela é rebatida com praticamente a mesma velocidade, porque o núcleo não pode se comprimir mais e a única opção é ricochetear o que o atinge. Mas essa primeira camada agora está voltando enquanto todas as outras estão vindo, elas irão se colidir possuindo tanto massa quanto velocidades fora de qualquer coisa que possamos imaginar. Tais choques serão tão fortes que poderemos formar todos os demais elementos da tabela periódica depois do ferro, todos resultantes da explosão de uma estrela que, nesse momento, está se tornando uma estrela de nêutrons (apenas aquele núcleo super denso vai sobrar, o resto explodiu e foi embora), essa explosão é conhecida como supernova.

Esse processo todo não é rápido. A estrela passa a maior parte do tempo “queimando” hidrogênio para fabricar hélio, menos tempo passando do hélio para o carbono e assim por diante, o tempo gasto em cada processo depende do tamanho dos átomos, sendo o que leva aos átomos mais pesados mais rápido. E também vale lembrar que o que descrevi é apenas um destino possível da estrela, a maneira como cada uma pode morrer é bem variada, depende da massa e de quem está na vizinhança.

A explosão de uma supernova libera muita matéria e, sendo ela dificilmente isolada, acaba se tornando ingrediente para a formação de novas estrelas. Não por menos, há regiões do espaço conhecidas como “berçário de estrelas”, locais de grande acúmulo de matéria onde a densidade limite é atingida com frequência e estrelas aparecem.

Se essa explosão acontece próxima à Terra, podemos ver com clareza o aparecimento de uma estrela muito brilhante durante três meses. Diversos povos na antiguidade relataram essas estrelas, sua luminosidade era tão intensa que uma noite de lua nova ainda era visível pela luz que essa explosão emitia. A última supernova próxima a Terra foi em 1986, e esses eventos são raros, é difícil haver mais que uma próxima a cada 400 anos.

No entanto, todos os elementos pesados que conhecemos, o ouro, a prata, a platina, o chumbo, o zinco do seu corpo, o cobre, o tungstênio que compõe o filamento de sua lâmpada, o mercúrio do termômetro, o iodo do seu sal, todos eles se formaram da explosão de uma estrela. Os mais leves que o ferro se formaram enquanto ela morria e são apenas liberados nessa explosão. Nisso, as estrelas são fábricas de átomos pesados, o que permite nosso universo de ser composto de mais que hidrogênio, e o que permite nossa existência, compostos desses átomos variados, uma intrincada rede de reações eletroquímicas e, em última análise, poeira das estrelas.

3 respostas